kinetická energie je energie pohybu. Výraz pro kinetickou energii je odvozen při pohledu na případ objektu, který je zvednut do určité relativní výšky (tak se na tomto objektu pracuje) a poté se nechá spadnout.
klíčové pojmy
o kinetická energie
cíle
o Odvozte výraz pro kinetickou energii z fyzikálního konceptu práce
o pochopte vztah práce a kinetické energie
o Vypočítejte kinetickou energii různých objektů
začněme!
vztahující se k práci a kinetické energii
v jistém smyslu je práce množství energie vložené do úkolu (nebo možná „vložené do objektu“). Například, představte si, že jsme vyzvednout nějaký objekt z podlahy a zvýšit ji do určité výšky; udělali jsme určité množství práce na tomto objektu. Pokud to však necháme jít, zrychlí se, jako by se práce, kterou jsme udělali při zvedání objektu, změnila v pohyb. Prostřednictvím tohoto příkladu můžeme odvodit definici kinetické energie, což je energie pohybu. Tato definice, jak uvidíme, úzce souvisí s tím, jak jsme definovali práci.
nejprve uvažujme objekt: míč o hmotnosti m. vybereme míč ze stolu a zvýšíme jej o vzdálenost h nad tímto stolem, jak je znázorněno níže. Proto jsme udělali množství práce W = mgh, (tento výsledek je součinem velikosti vektoru posunutí (h) a aplikované síly (mg) – odpovídající vektory jsou rovnoběžné).
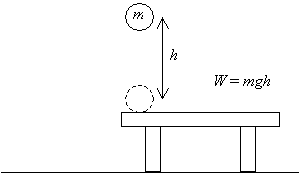
nyní, pokud uvolníme tuto kouli a necháme ji spadnout z výšky h nad stolem, jakmile se vrátí do své původní výšky (úroveň stolu), bude mít určitou rychlost v vyplývající ze zrychlení v důsledku gravitace.
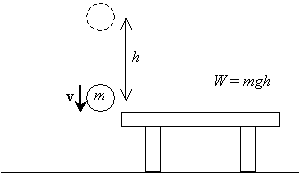
chceme vypočítat tuto rychlost (nebo rychlost, technicky-můžeme občas nahradit termín rychlost pro rychlost, ale vždy mějte na paměti, že rychlost je ve skutečnosti vektor a rychlost je velikost rychlosti). Víme, že zrychlení způsobené gravitací je konstantní a že počáteční rychlost koule je nulová (před uvolněním je stacionární). Předpokládáme, že počáteční výška míče je h a že její konečná výška je nula (úroveň stolu). Pro výpočet rychlosti odvozením příslušných vzorců požadujeme použití elementárního integrálního počtu. (Pokud jste pokročilý student nebo hledáte další výzvu, můžete se pokusit odvodit tyto vzorce za výše uvedených podmínek sami. Stačí si uvědomit, že rychlost v koule je časová rychlost změny její polohy x jako funkce času t, ![]() a že zrychlení a je časová rychlost změny rychlosti,
a že zrychlení a je časová rychlost změny rychlosti, ![]() .)
.)
![]()
![]()
tyto vzorce vyjadřují rychlost jako funkci času, v(t) a polohu (výšku) jako funkci času, x (t), pokud jde o zrychlení a, výšku h a čas t. víme, že A = –g, protože míč je zrychlen pouze gravitací a toto zrychlení je směrem dolů (odtud záporné znaménko). Konečná Poloha míče je nula metrů nebo x (t) = 0. Vypočítejme t, dobu mezi uvolněním míče a jeho příchodem na úroveň stolu.
![]()
![]()
![]()
nyní vypočítáme rychlost míče v tomto okamžiku.
![]()
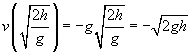
pojďme nyní porovnat tento výsledek s prací původně provedenou na objektu: W = mgh. Všimněte si, jak blízko ve formě jsou tyto dva výrazy; ve skutečnosti jediným faktorem, který chybí z rychlosti, je hmotnost míče, m. Pokud bychom na druhou rychlost vynásobili m a poté vydělili 2, měli bychom ve skutečnosti stejný výraz jako práce!
![]()
můžeme tedy v jistém smyslu vidět, jak lze odvodit definici kinetické energie. Kinetická energie k objektu, pak, je skalár definovaný následovně, kde m je hmotnost objektu a v je jeho rychlost:
![]()
jak se ukazuje, kinetická energie je práce na objektu pomocí čisté síly na tento objekt. Ačkoli tedy žena může na objektu vykonávat určité množství práce tím, že jej zvedne z jedné výšky do druhé, čistá síla na tento objekt je nulová (žena aplikuje sílu rovnou, ale opačnou ve směru gravitace). Nedochází tedy ke změně kinetické energie. Pokud je tento objekt uvolněn a nechá se spadnout, získává kinetickou energii, protože čistá síla na něm je prostě gravitační (jediná síla). Abychom pochopili vztah kinetické energie a práce, musíme trochu vylepšit náš koncept práce. Pokud definujeme práci W jako celkovou práci provedenou na objektu všemi silami (jinými slovy práce provedená na objektu čistou silou), pak platí následující vztah mezi prací W a počáteční a konečnou kinetickou energií (Ki a Kf).
![]() kde
kde ![]()
čistá práce provedená na objektu se tedy rovná změně kinetické energie tohoto objektu (ΔK). Následující praktické problémy vám poskytují příležitost vyzkoušet a aplikovat své chápání pojmů práce a kinetické energie.
Praxe Problém: Projektil o hmotnosti 1 kilogram cestuje rychlostí 5 metrů za sekundu. Jakou rychlostí musí projektil 0, 1 kilogramu cestovat, aby dosáhl stejné kinetické energie?
řešení: nejprve vypočítáme kinetickou energii masivnějšího (1 kilogram) projektilu.
![]()
nyní můžeme vypočítat rychlost méně masivního objektu tak, že má stejnou kinetickou energii, k.
![]()
![]()
![]()
cvičný problém: muž zvedne 15kilogramovou váhu do výšky dvou metrů nad zemí, než ji upustí. V okamžiku, než se váha dostane do kontaktu se zemí, jaká je její rychlost?
řešení: nakreslíme diagram znázorňující síly působící na objekt při jeho zvedání a pádu; tyto síly zahrnují gravitaci (Fg) a vzestupnou sílu, kterou člověk aplikuje (Fu).
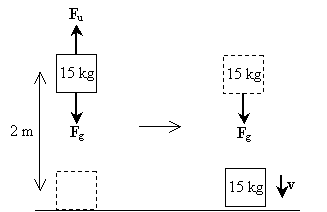
Všimněte si, že první krok procesu (zvedání váhy) nezahrnuje žádnou čistou sílu působící na objekt-síla způsobená gravitací je vyvážena silou, kterou člověk aplikuje při zvedání váhy. Ve druhém kroku však váha zažívá pouze gravitační sílu. Čistá síla je tedy v tomto případě mg ve směru dolů. Jako taková je rychlost objektu také ve směru dolů. Práce na hmotnosti v důsledku gravitace je prostě mgh; to je také celková práce na hmotnosti v průběhu celého procesu. Všimněte si, že počáteční kinetická energie hmotnosti je nulová, protože má nulovou rychlost. Pojďme nyní vypočítat rychlost použitím vztahu mezi čistou prací a změnou kinetické energie.