Data Science od základů
budování intuice pro to, jak KNN modely pracují
Data science nebo Aplikovaná statistika kurzy obvykle začínají lineárními modely, ale svým způsobem, k-nejbližší sousedé je pravděpodobně nejjednodušší široce používaný model koncepčně. KNN modely jsou opravdu jen technické implementace společné intuice, že věci, které sdílejí podobné rysy, mají tendenci být, studna, podobné. To je stěží hluboký vhled, přesto tyto praktické implementace mohou být extrémně silné, a, rozhodující pro někoho, kdo se blíží k neznámému datovému souboru, zvládne nelinearity bez složitého datového inženýrství nebo nastavení modelu.
co
jako ilustrativní příklad uvažujme nejjednodušší případ použití modelu KNN jako klasifikátoru. Řekněme, že máte datové body, které spadají do jedné ze tří tříd. Dvourozměrný příklad může vypadat takto:

pravděpodobně jasně vidíte, že různé třídy jsou seskupeny — zdá se, že levý horní roh grafů patří do oranžové třídy, pravá/střední část do modré třídy. Pokud jste dostali souřadnice nového bodu někde v grafu a zeptali jste se, do které třídy pravděpodobně patří, odpověď by byla většinou jasná. Jakýkoli bod v levém horním rohu grafu bude pravděpodobně oranžový atd.
úkol se stává o něco méně jistý mezi třídami, nicméně, kde se musíme usadit na hranici rozhodnutí. Zvažte nový bod přidaný červeně níže:

měl by být tento nový bod klasifikován jako oranžový nebo modrý? Zdá se, že bod spadá mezi dva shluky. Vaše první intuice může být vybrat cluster, který je blíže k novému bodu. To by byl přístup „nejbližšího souseda“, a přestože je koncepčně jednoduchý, často přináší docela rozumné předpovědi. Který dříve identifikovaný bod je nový bod nejblíže? Nemusí být zřejmé, že pouhým pohledem na graf je odpověď, ale pro počítač je snadné projít body a dát nám odpověď:

vypadá to, že nejbližší bod je v modré kategorii, takže náš nový bod je pravděpodobně také. To je metoda nejbližšího souseda.
v tomto okamžiku se možná divíte, k čemu je “ k “ v k-nejbližších sousedech. K je počet blízkých bodů, na které se model podívá při hodnocení nového bodu. V našem nejjednodušším příkladu nejbližšího souseda byla tato hodnota pro k jednoduše 1-podívali jsme se na nejbližšího souseda a to bylo vše. Mohli jste se však rozhodnout podívat se na nejbližší 2 nebo 3 body. Proč je to důležité a proč by někdo nastavil k na vyšší číslo? Pro jednu věc, hranice mezi třídami by se mohly narazit vedle sebe způsoby, díky nimž je méně zřejmé, že nejbližší bod nám dá správnou klasifikaci. Zvažte modré a zelené oblasti v našem příkladu. Ve skutečnosti, pojďme přiblížit na ně:

Všimněte si, že zatímco celkové regiony se zdají dost odlišné, jejich hranice se zdají být trochu propletené. Toto je společná vlastnost datových sad s trochou šumu. Když tomu tak je, je těžší klasifikovat věci v hraničních oblastech. Zvažte tento nový bod:

na jedné straně vizuálně rozhodně vypadá, že nejbližší dříve identifikovaný bod je modrý, což nám náš počítač může snadno potvrdit:

na druhé straně se tento nejbližší modrý bod jeví jako trochu odlehlý, daleko od středu modré oblasti a tak nějak obklopen zelenými body. A tento nový bod je dokonce na vnější straně tohoto modrého bodu! Co kdybychom se podívali na tři nejbližší body k novému červenému bodu?

nebo dokonce nejbližších pět bodů k novému bodu?

se nyní zdá, že náš nový bod je v zelené čtvrti! Stalo se, že má blízký modrý bod, ale převaha nebo blízké body jsou zelené. V tomto případě, možná by mělo smysl nastavit vyšší hodnotu pro k, podívat se na hrst blízkých bodů a nechat je nějak hlasovat o predikci nového bodu.
ilustrovaný problém je příliš vhodný. Když je k nastavena na jednu, hranice, mezi nimiž jsou oblasti identifikovány algoritmem jako modrá a zelená, je hrbolatá, hadí se tam s každým jednotlivým bodem. Červený bod vypadá, jako by to mohlo být v modré oblasti:

přináší k až 5, nicméně vyhlazuje rozhodovací hranici při hlasování o různých blízkých bodech. Červený bod se nyní zdá pevně v zelené čtvrti:

kompromisem s vyššími hodnotami k je ztráta zrnitosti v rozhodovací hranici. Nastavení k velmi vysoké bude mít tendenci vám hladké hranice, ale hranice skutečného světa, které se snažíte modelovat, nemusí být dokonale hladké.
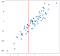
prakticky můžeme použít stejný druh přístupu nejbližších sousedů pro regrese, kde chceme spíše individuální hodnotu než klasifikaci. Zvažte následující regresi níže:

data byla náhodně generována, ale byla generována jako lineární, takže lineární regresní model by přirozeně dobře zapadal do těchto dat. Chci však zdůraznit, že výsledky lineární metody můžete přiblížit koncepčně jednodušším způsobem s přístupem k-nejbližších sousedů. Naše „regrese“ v tomto případě nebude jediným vzorcem, jaký by nám dal model OLS, ale spíše nejlépe předpovězenou výstupní hodnotou pro daný vstup. Zvažte hodnotu -.75 na ose x, kterou jsem označil svislou čarou:

bez řešení rovnic můžeme dospět k rozumné aproximaci toho, jaký by měl být výstup, pouhým zvážením blízkých bodů:

dává smysl, že předpokládaná hodnota by měla být v blízkosti těchto bodů, ne mnohem nižší nebo vyšší. Možná by dobrá předpověď byla průměr těchto bodů:
můžete si představit, že to děláte pro všechny možné vstupní hodnoty a přicházíte s předpověďmi všude:

spojení všech těchto předpovědí s čárou nám dává naši regresi:

v tomto případě nejsou výsledky čistou čarou, ale poměrně dobře sledují vzestupný sklon dat. To se nemusí zdát strašně působivé, ale jednou z výhod jednoduchosti této implementace je to, že zvládá nelinearitu dobře. Zvažte tuto novou sbírku bodů:
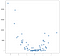
tyto body byly generovány pouhým umocněním hodnot z předchozího příkladu, ale předpokládejme, že jste narazili na takovou datovou sadu ve volné přírodě. Je to samozřejmě není lineární povahy a zatímco model OLS stylu lze snadno zpracovat tento druh dat, to vyžaduje použití nelineárních nebo interakčních termínů, což znamená, že data vědec musí učinit některá rozhodnutí o tom, jaký druh datového inženýrství provést. Přístup KNN nevyžaduje žádná další rozhodnutí-stejný kód, který jsem použil na lineárním příkladu, lze zcela znovu použít na nová data, aby se získala funkční sada předpovědí:

stejně jako u příkladů klasifikátoru, nastavení vyšší hodnoty k nám pomáhá vyhnout se nadměrnému vybavení, i když můžete začít ztrácet prediktivní sílu na okraji, zejména kolem okrajů vaší datové sady. Zvažte první příklad datové sady s předpověďmi provedenými s k nastavenou na jednu, to je přístup nejbližšího souseda:

naše předpovědi skočí nepravidelně, když model skočí z jednoho bodu v datovém souboru do druhého. Naproti tomu, nastavení K na deset, takže celkem deset bodů je zprůměrováno dohromady pro predikci, což přináší mnohem plynulejší jízdu:

obecně to vypadá lépe,ale na okrajích dat. Protože náš model bere v úvahu tolik bodů pro jakoukoli danou předpověď, když se dostaneme blíže k jednomu z okrajů našeho vzorku, naše předpovědi se začnou zhoršovat. Tento problém můžeme řešit poněkud vážením našich předpovědí k bližším bodům, i když to přichází s vlastními kompromisy.
jak
při nastavování modelu KNN existuje pouze několik parametrů, které je třeba vybrat/lze vylepšit, aby se zlepšil výkon.
K: počet sousedů: Jak bylo diskutováno, zvýšení K bude mít tendenci vyhlazovat hranice rozhodování, vyhnout se nadměrnému vybavení za cenu nějakého řešení. Neexistuje žádná jediná hodnota k, která bude fungovat pro každou datovou sadu. Pro klasifikační modely, zejména pokud existují pouze dvě třídy, liché číslo je obvykle vybráno pro k. to je tak, že algoritmus nikdy nenarazí na „kravatu“: např. podívá se na nejbližší čtyři body a zjistí, že dva z nich jsou v modré kategorii a dva v červené kategorii.
metrická vzdálenost: Jak se ukazuje, existují různé způsoby, jak měřit, jak „blízko“ jsou dva body k sobě, a rozdíly mezi těmito metodami mohou být významné ve vyšších dimenzích. Nejčastěji se používá euklidovská vzdálenost, Standardní druh, který jste se možná naučili na střední škole pomocí Pythagorovy věty. Další metrikou je takzvaná „Manhattan distance“, která měří vzdálenost v každém kardinálním směru, spíše než podél úhlopříčky (jako byste šli z jedné křižovatky ulic Na Manhattanu do druhé a museli jste sledovat pouliční mřížku, než abyste byli schopni vzít nejkratší trasu „jako vrána letí“). Obecněji, to jsou vlastně obě formy toho, co se nazývá „Minkowski vzdálenost“, jehož vzorec je:

když je p nastaveno na 1, tento vzorec je stejný jako Manhattanská vzdálenost, a když je nastaven na dvě, euklidovská vzdálenost.
váhy: jedním ze způsobů, jak vyřešit problém možné „vazby“, když algoritmus hlasuje o třídě, a problém, kdy se naše regresní předpovědi zhoršily směrem k okrajům datové sady, je zavedení vážení. S váhami budou blízké body počítat více než body dále. Algoritmus se bude stále dívat na všechny nejbližší sousedy k, ale bližší sousedé budou mít více hlasů než ti vzdálenější. Toto není dokonalé řešení a přináší možnost opětovného přefiknutí. Vezměme si náš regresní příklad, tentokrát s váhami:

naše předpovědi jdou hned na okraj datové sady, ale můžete vidět, že naše předpovědi se nyní pohybují mnohem blíže k jednotlivým bodům. Vážená metoda funguje poměrně dobře, když jste mezi body, ale jak se blížíte k určitému bodu, hodnota tohoto bodu má stále větší vliv na predikci algoritmu. Pokud se dostanete dostatečně blízko k bodu, je to skoro jako nastavení k na jednu, protože tento bod má tolik vlivu.
škálování / normalizace: poslední, ale zásadně důležité je, že KNN modely mohou být odhozeny, pokud mají různé proměnné funkcí velmi odlišné stupnice. Vezměme si model, který se snaží předpovědět, říci, prodejní cena domu na trhu na základě funkcí, jako je počet ložnic a celkové rozlohy domu, atd. V počtu čtverečních stop v domě je větší rozdíl než v počtu ložnic. Typicky, domy mají jen malou hrstku ložnic, a ani největší sídlo nebude mít desítky nebo stovky ložnic. Čtverečních stop, na druhé straně, jsou relativně malé, takže domy se mohou pohybovat v blízkosti, říci, 1,000 čtverečních feat na Malé Straně desítky tisíc čtverečních stop na velké straně.
zvažte srovnání mezi 2 000 čtverečních stop domu s 2 ložnicemi a 2 010 čtverečních stop domu se dvěma ložnicemi-10 čtverečních. nohy sotva dělají rozdíl. Naproti tomu dům o rozloze 2 000 čtverečních metrů se třemi ložnicemi je velmi odlišný a představuje velmi odlišné a možná stísněnější uspořádání. Naivní počítač by však neměl kontext, aby to pochopil. Říká se, že ložnice 3 je pouze „jedna“ jednotka od ložnice 2, zatímco zápatí 2,010 sq je „deset“ od zápatí 2,000 sq. Aby se tomu zabránilo, data funkcí by měla být zmenšen před implementací modelu KNN.
silné a slabé stránky
modely KNN se snadno implementují a dobře zvládají nelinearity. Montáž modelu má také tendenci být rychlá: počítač nakonec nemusí počítat žádné konkrétní parametry nebo hodnoty. Kompromis je, že zatímco model je rychle nastavit, je to pomalejší předvídat, protože s cílem předpovědět výsledek pro novou hodnotu, bude muset prohledávat všechny body v jeho tréninkové sady najít ty nejbližší. Pro velké datové sady, KNN proto může být relativně pomalá metoda ve srovnání s jinými regresemi, které mohou trvat déle, než se vejdou, ale poté provedou své předpovědi relativně přímými výpočty.
dalším problémem modelu KNN je, že postrádá interpretovatelnost. Lineární regrese OLS bude mít jasně interpretovatelné koeficienty, které samy o sobě mohou naznačovat „velikost účinku“ daného prvku (i když při přiřazování kauzality je třeba postupovat opatrně). Zeptat se, které funkce mají největší účinek, však pro model KNN nedává smysl. Částečně kvůli tomu, KNN modely také nemohou být ve skutečnosti použity pro výběr funkcí, způsobem, jakým může být lineární regrese s přidaným nákladovým funkčním výrazem, jako je ridge nebo laso, nebo způsobem, jakým rozhodovací strom implicitně vybírá, které funkce se zdají nejcennější.