det grundlæggende: KNN til klassificering og regression

datavidenskab fra bunden

datalogi eller anvendte statistikkurser starter typisk med lineære modeller, men på sin måde er K-nærmeste naboer sandsynligvis den enkleste udbredte model konceptuelt. KNN-modeller er egentlig bare tekniske implementeringer af en fælles intuition, at ting, der deler lignende funktioner, har tendens til at være, godt, lignende. Dette er næppe en dyb indsigt, alligevel kan disse praktiske implementeringer være ekstremt kraftfulde, og, afgørende for nogen, der nærmer sig et ukendt datasæt, kan håndtere ikke-lineariteter uden nogen kompliceret Datateknik eller modelopsætning.

hvad

som et illustrativt eksempel, lad os overveje det enkleste tilfælde at bruge en KNN-model som klassifikator. Lad os sige, at du har datapunkter, der falder i en af tre klasser. Et todimensionelt eksempel kan se sådan ud:

du kan sandsynligvis se temmelig tydeligt, at de forskellige klasser er grupperet sammen — det øverste venstre hjørne af graferne ser ud til at tilhøre den orange klasse, højre/midterste sektion til den blå klasse. Hvis du fik koordinaterne for nyt punkt et eller andet sted på grafen og spurgte, hvilken klasse det sandsynligvis ville tilhøre, det meste af tiden ville svaret være ret klart. Ethvert punkt i øverste venstre hjørne af grafen er sandsynligvis orange osv.

opgaven bliver dog lidt mindre sikker mellem klasserne, hvor vi er nødt til at slå os ned på en beslutningsgrænse. Overvej det nye punkt tilføjet i rødt nedenfor:

skal dette nye punkt klassificeres som orange eller blå? Pointen ser ud til at falde ind mellem de to klynger. Din første intuition kan være at vælge den klynge, der er tættere på det nye punkt. Dette ville være den’ nærmeste nabo ‘ tilgang, og på trods af at den er konceptuelt enkel, giver den ofte ret fornuftige forudsigelser. Hvilket tidligere identificeret punkt er det nye punkt tættest på? Det kan ikke være indlysende bare eyeballing grafen, hvad svaret er, men det er nemt for computeren at køre gennem de punkter og give os et svar:

ser det ud til, at det nærmeste punkt er i den blå kategori, så vores nye punkt er sandsynligvis også. Det er den nærmeste nabo metode.

på dette tidspunkt undrer du dig måske over, hvad ‘k’ i k-nærmeste naboer er til. K er antallet af nærliggende punkter, som modellen vil se på, når man vurderer et nyt punkt. I vores enkleste nærmeste naboeksempel var denne værdi for k simpelthen 1-Vi kiggede på den nærmeste nabo, og det var det. Du kunne dog have valgt at se på de nærmeste 2 eller 3 point. Hvorfor er dette vigtigt, og hvorfor skulle nogen sætte k til et højere tal? For det første kan grænserne mellem klasser støde op ved siden af hinanden på måder, der gør det mindre indlysende, at det nærmeste punkt giver os den rigtige klassificering. Overvej de blå og grønne regioner i vores eksempel. Faktisk, lad os forstørre dem:

Bemærk, at mens de samlede regioner synes adskilte nok, synes deres grænser at være lidt sammenflettet med hinanden. Dette er et fælles træk ved datasæt med lidt støj. Når dette er tilfældet, bliver det sværere at klassificere ting i grænseområderne. Overvej dette nye punkt:

på den ene side ser det visuelt ud til, at det nærmeste tidligere identificerede punkt er blåt, som vores computer let kan bekræfte for os:

på den anden side virker det nærmeste blå punkt som en smule af en outlier selv, langt væk fra centrum af den blå region og slags omgivet af grønne punkter. Og dette nye punkt er endda på ydersiden af det blå punkt! Hvad hvis vi kiggede på de tre nærmeste punkter til det nye røde punkt?

eller endda de nærmeste fem punkter til det nye punkt?

nu ser det ud til, at vores nye punkt er i et grønt kvarter! Det skete at have et nærliggende blåt punkt, men overvægten eller nærliggende punkter er grønne. I dette tilfælde, måske ville det være fornuftigt at indstille en højere værdi for k, at se på en håndfuld nærliggende punkter og få dem til at stemme på en eller anden måde om forudsigelsen for det nye punkt.

det problem, der illustreres, er overtilpasset. Når k er indstillet til en, er grænsen mellem hvilke regioner der identificeres af algoritmen som blå og grøn ujævn, det slanger frem med hvert enkelt punkt. Det røde punkt ser ud som om det kan være i den blå region:

at bringe k op til 5 udjævner imidlertid beslutningsgrænsen, når de forskellige nærliggende punkter stemmer. Det røde punkt virker nu fast i det grønne kvarter:

afvejningen med højere værdier af k er tabet af granularitet i beslutningsgrænsen. Indstilling k meget høj vil have en tendens til at give dig glatte grænser, men de virkelige verdensgrænser, du prøver at modellere, er muligvis ikke helt glatte.

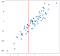
Praktisk set kan vi bruge den samme slags nærmeste nabo tilgang til regressioner, hvor vi ønsker en individuel værdi snarere end en klassificering. Overvej følgende regression nedenfor:

dataene blev tilfældigt genereret, men blev genereret til at være lineære, så en lineær regressionsmodel ville naturligvis passe godt til disse data. Jeg vil dog gerne påpege, at du kan tilnærme resultaterne af den lineære metode på en konceptuelt enklere måde med en K-nærmeste naboer tilgang. Vores ‘regression’ i dette tilfælde vil ikke være en enkelt formel som en OLS-model ville give os, men snarere en bedst forudsagt outputværdi for et givet input. Overvej værdien af -.75 på h-aksen, som jeg har markeret med en lodret linje:

uden at løse nogen ligninger kan vi komme til en rimelig tilnærmelse af, hvad output skal være bare ved at overveje de nærliggende punkter:

det giver mening, at den forudsagte værdi skal være nær disse punkter, ikke meget lavere eller højere. Måske ville en god forudsigelse være gennemsnittet af disse punkter:

du kan forestille dig at gøre dette for alle mulige inputværdier og komme med forudsigelser overalt:

at forbinde alle disse forudsigelser med en linje giver os vores regression:

i dette tilfælde er resultaterne ikke en ren linje, men de sporer den opadgående hældning af dataene rimeligt godt. Dette virker måske ikke forfærdeligt imponerende, men en fordel ved enkelheden ved denne implementering er, at den håndterer ikke-linearitet godt. Overvej denne nye samling af point:

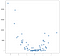
disse punkter blev genereret ved blot at kvadrere værdierne fra det foregående eksempel, men antag at du stødte på et datasæt som dette i naturen. Det er naturligvis ikke lineært, og mens en OLS-stilmodel nemt kan håndtere denne slags data, kræver det brug af ikke-lineære eller interaktionsudtryk, hvilket betyder, at dataforskeren skal træffe nogle beslutninger om, hvilken slags Datateknik der skal udføres. KNN-tilgangen kræver ingen yderligere beslutninger – den samme kode, som jeg brugte på det lineære eksempel, kan genbruges helt på de nye data for at give et brugbart sæt forudsigelser:

som med klassificeringseksemplerne, indstilling af en højere værdi k hjælper os med at undgå overfit, selvom du måske begynder at miste forudsigelig strøm på margenen, især rundt om kanterne på dit datasæt. Overvej det første eksempel datasæt med forudsigelser lavet med k indstillet til en, det er en nærmeste nabo tilgang:

vores forudsigelser hopper uregelmæssigt rundt, da modellen hopper fra et punkt i datasættet til det næste. Derimod, indstilling k på ti, således at ti samlede point i gennemsnit sammen for forudsigelse giver en meget glattere tur:

generelt ser det bedre ud, men du kan se noget af et problem i kanterne af dataene. Fordi vores model tager så mange punkter i betragtning for en given forudsigelse, når vi kommer tættere på en af kanterne af vores prøve, begynder vores forudsigelser at blive værre. Vi kan løse dette problem noget ved at vægte vores forudsigelser til de nærmere punkter, selvom dette kommer med sine egne kompromiser.

hvordan

ved opsætning af en KNN-model er der kun en håndfuld parametre, der skal vælges/kan justeres for at forbedre ydeevnen.

K: antallet af naboer: Som diskuteret, stigende K vil have en tendens til at udjævne beslutningsgrænser, undgå overfit på bekostning af en vis opløsning. Der er ingen enkelt værdi af k, der fungerer for hvert enkelt datasæt. For klassificeringsmodeller, især hvis der kun er to klasser, vælges normalt et ulige tal for k. Dette er så algoritmen løber aldrig ind i et ‘slips’: f.eks. ser det på de nærmeste fire punkter og finder ud af, at to af dem er i den blå kategori og to er i den røde kategori.

afstand metrisk: Der er, som det viser sig, forskellige måder at måle, hvor ‘tæt’ to punkter er på hinanden, og forskellene mellem disse metoder kan blive betydelige i højere dimensioner. Mest almindeligt anvendte er euklidisk afstand, den standard sortering, du måske har lært i mellemskolen ved hjælp af Pythagoras sætning. En anden måling er såkaldt ‘Manhattan distance’, som måler afstanden taget i hver kardinalretning snarere end langs diagonalen (som om du gik fra et gadekryds på Manhattan til et andet og måtte følge gadenettet i stedet for at være i stand til at tage den korteste’ som kragen flyver ‘ rute). Mere generelt er disse faktisk begge former for det, der kaldes ‘Minkovski-afstand’, hvis formel er:

når p er indstillet til 1, er denne formel den samme som Manhattan-afstand, og når den er indstillet til to, euklidisk afstand.

vægte: en måde at løse både spørgsmålet om et muligt ‘slips’, når algoritmen stemmer på en klasse, og spørgsmålet, hvor vores regressionsforudsigelser blev værre mod kanterne af datasættet, er ved at indføre vægtning. Med vægte tæller de nærmeste punkter mere end punkterne længere væk. Algoritmen vil stadig se på alle K nærmeste naboer, men de tættere naboer vil have mere af en stemme end dem længere væk. Dette er ikke en perfekt løsning og giver mulighed for overfitting igen. Overvej vores regressionseksempel, denne gang med vægte:

vores forudsigelser går lige til kanten af datasættet nu, men du kan se, at vores forudsigelser nu svinger meget tættere på de enkelte punkter. Den vægtede metode fungerer rimeligt godt, når du er mellem punkter, men når du kommer tættere og tættere på et bestemt punkt, har dette punkts værdi mere og mere indflydelse på algoritmens forudsigelse. Hvis du kommer tæt nok på et punkt, er det næsten som at sætte k til en, da dette punkt har så stor indflydelse.

skalering/normalisering: et sidste, men afgørende vigtigt punkt er, at KNN-modeller kan smides ud, hvis forskellige funktionsvariabler har meget forskellige skalaer. Overvej en model, der forsøger at forudsige, sige, salgsprisen for et hus på markedet baseret på funktioner som antallet af soveværelser og den samlede firkantede optagelser af huset, etc. Der er mere variation i antallet af kvadratmeter i et hus end der er i antallet af soveværelser. Typisk, huse har kun en lille håndfuld soveværelser, og ikke engang det største palæ vil have titusinder eller hundreder af soveværelser. Kvadratfod er derimod relativt små, så huse kan variere fra tæt på 1.000 kvadratfod på den lille side til titusinder af kvadratfod på den store side.

overvej sammenligningen mellem et 2.000 kvadratmeter hus med 2 soveværelser og et 2.010 kvadratmeter hus med to soveværelser — 10 kvm. fødder gør næppe en forskel. I modsætning hertil er et hus på 2.000 kvadratmeter med tre soveværelser meget anderledes og repræsenterer et meget anderledes og muligvis mere trangt layout. En naiv computer ville dog ikke have konteksten til at forstå det. Det vil sige, at 3 soveværelset kun er ‘en’ enhed væk fra 2 soveværelset, mens 2.010 kvadratfod er ‘ti’ væk fra 2.000 kvadratfod. For at undgå dette skal funktionsdata skaleres, før en KNN-model implementeres.

styrker og svagheder

KNN-modeller er nemme at implementere og håndtere ikke-lineariteter godt. Montering af modellen har også en tendens til at være hurtig: computeren behøver trods alt ikke at beregne nogen bestemte parametre eller værdier. Afvejningen her er, at mens modellen er hurtig at konfigurere, er den langsommere at forudsige, da den for at forudsige et resultat for en ny værdi skal søge gennem alle punkterne i sit træningssæt for at finde de nærmeste. For store datasæt kan KNN derfor være en relativt langsom metode sammenlignet med andre regressioner, der kan tage længere tid at passe, men derefter foretage deres forudsigelser med relativt enkle beregninger.

et andet problem med en KNN-model er, at den mangler fortolkningsevne. En OLS lineær regression vil have klart fortolkelige koefficienter, der selv kan give en indikation af ‘effektstørrelsen’ af en given funktion (skønt der skal udvises en vis forsigtighed ved tildeling af årsagssammenhæng). At spørge, hvilke funktioner der har den største effekt, giver dog ikke rigtig mening for en KNN-model. Dels på grund af dette kan KNN-modeller heller ikke rigtig bruges til funktionsvalg, på den måde, at en lineær regression med et ekstra omkostningsfunktionsudtryk, som ridge eller lasso, kan være, eller den måde, som et beslutningstræ implicit vælger, hvilke funktioner der synes mest værdifulde.