kinetisk energi er bevægelsesenergien. Et udtryk for kinetisk energi er afledt ved at se på sagen om et objekt, der løftes til en vis relativ højde (således arbejdes der på dette objekt) og derefter får lov til at falde.
nøgleord
O kinetisk energi
mål
O udlede et udtryk for kinetisk energi fra fysikbegrebet arbejde
O forstå forholdet mellem arbejde og kinetisk energi
O Beregn kinetisk energi fra forskellige objekter
lad os begynde!
vedrørende arbejde og kinetisk energi
i en vis forstand er arbejde den mængde energi, der sættes i en opgave (eller måske “sat i objektet”). For eksempel, forestil dig, at vi henter noget objekt fra gulvet og hæver det til en bestemt højde; vi har gjort en vis mængde arbejde på dette objekt. Hvis vi lader det gå, accelererer det imidlertid, som om det arbejde, vi gjorde med at løfte objektet, bliver til bevægelse. Gennem dette eksempel kan vi udlede en definition for kinetisk energi, som er bevægelsesenergi. Denne definition, som vi vil se, er tæt knyttet til, hvordan vi har defineret arbejde.
lad os først overveje et objekt: en kugle af masse m. vi henter bolden op fra et bord og hæver det en afstand h over det bord, som vist nedenfor. Vi har derfor udført en mængde arbejde V = mgh, (dette resultat er produktet af størrelsen af forskydningsvektoren (h) og den påførte kraft (mg) – de tilsvarende vektorer er parallelle).
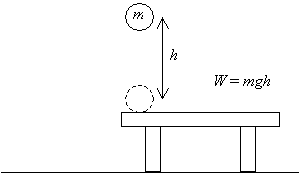
nu, hvis vi frigiver den bold og lader den falde fra højden h over bordet, når den vender tilbage til sin oprindelige højde (bordets niveau), vil den have en vis hastighed v som følge af accelerationen på grund af tyngdekraften.
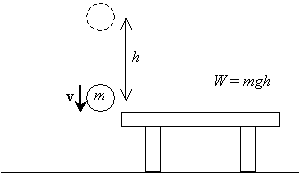
vi ønsker at beregne denne hastighed (eller hastighed, teknisk-Vi kan lejlighedsvis erstatte udtrykket hastighed for hastighed, men vær altid opmærksom på, at hastighed faktisk er en vektor, og hastighed er størrelsen af hastigheden). Vi ved, at accelerationen på grund af tyngdekraften er konstant, og at kuglens indledende hastighed er nul (den er stationær, før den frigives). Vi antager, at kuglens indledende højde er h, og at dens endelige højde er nul (bordets niveau). For at beregne hastigheden ved at udlede de relevante formler kræver vi brug af elementær integreret beregning. (Hvis du er en avanceret studerende eller leder efter en ekstra udfordring, kan du selv prøve at udlede disse formler under ovenstående betingelser. Bemærk blot, at kuglens hastighed V er tidshastigheden for ændring af dens position som en funktion af tid t, ![]() , og at accelerationen A er tidshastigheden for ændring af hastigheden,
, og at accelerationen A er tidshastigheden for ændring af hastigheden, ![]() .)
.)
![]()
![]()
disse formler udtrykker hastigheden som en funktion af tiden, v (t) og positionen(højden) som en funktion af tiden, H (t), med hensyn til accelerationen a, højden h og tiden t. vi ved, at a = –g, da bolden kun accelereres af tyngdekraften, og denne acceleration er nedad (deraf det negative tegn). Den endelige position af bolden er nul meter, eller H(t) = 0. Lad os beregne t, mængden af tid mellem boldens frigivelse og dens ankomst til bordets niveau.
![]()
![]()
![]()
lad os nu beregne kuglens hastighed på dette tidspunkt.
![]()
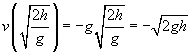
lad os nu sammenligne dette resultat med det arbejde, der oprindeligt blev udført på objektet: V = mgh. Bemærk, hvor tæt i form disse to udtryk er; faktisk, den eneste faktor, der mangler i hastigheden, er kuglens masse, m. hvis vi kvadrerede hastigheden, ganget med m, og derefter divideret med 2, Vi ville faktisk have det samme udtryk som værket!
![]()
Således kan vi på en eller anden måde se, hvordan definitionen af kinetisk energi kan udledes. Det kinetisk energi K af et objekt, derefter, er en skalar defineret som følger, hvor m er objektets masse og v er dens hastighed:
![]()
som det viser sig, er den kinetiske energi det arbejde, der udføres på et objekt af nettokraften på det objekt. Selvom en kvinde kan udføre en vis mængde arbejde på et objekt ved at løfte det fra en højde til en anden, er nettokraften på det objekt nul (kvinden anvender en kraft, der er lig med, men modsat i tyngderetningen). Der er således ingen ændring i kinetisk energi. Hvis dette objekt frigives og får lov til at falde, får det imidlertid kinetisk energi, fordi nettokraften på det simpelthen er tyngdekraften (en enkelt kraft). For at forstå forholdet mellem kinetisk energi og arbejde skal vi således forfine vores koncept om arbejde noget. Hvis vi definerer arbejdet H som det samlede arbejde, der udføres på objektet af alle kræfter (med andre ord det arbejde, der udføres på objektet af nettokraften), holder følgende forhold mellem arbejdet H og de indledende og endelige kinetiske energier (Ki og Kf).
![]() hvor
hvor ![]()
således er det nettoarbejde, der udføres på et objekt, lig med ændringen i objektets kinetiske energi (prikk). Følgende praksisproblemer giver dig mulighed for at teste og anvende din forståelse af begreberne arbejde og kinetisk energi.
Praksis Problem: Et projektil af Masse 1 kilo rejser med 5 meter pr. Hvilken hastighed skal et projektil på 0,1 kg køre for at opnå den samme kinetiske energi?
løsning: lad os først beregne den kinetiske energi af det mere massive (1 kg) projektil.
![]()
vi kan nu beregne hastigheden på det mindre massive objekt, så det har den samme kinetiske energi, K.
![]()
![]()
![]()
Øvelsesproblem: en mand løfter en vægt på 15 kg til en højde på to meter væk fra jorden, før han taber den. I øjeblikket før vægten kommer i kontakt med jorden, Hvad er dens hastighed?
løsning: lad os tegne et diagram, der illustrerer de kræfter, der virker på objektet, når det løftes og når det falder; disse kræfter inkluderer tyngdekraften (Fg) og den opadgående kraft, som manden anvender (Fu).
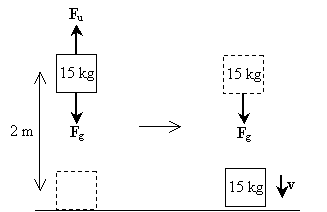
Bemærk, at det første trin i processen (løfte vægten) involverer ingen nettokraft, der virker på objektet-kraften på grund af tyngdekraften afbalanceres af den kraft, som manden anvender til at løfte vægten. I det andet trin oplever vægten imidlertid kun tyngdekraften. Nettokraften er i dette tilfælde derfor mg i nedadgående retning. Som sådan er objektets hastighed også i nedadgående retning. Det arbejde, der udføres på vægten som følge af tyngdekraften, er simpelthen mgh; dette er også det samlede arbejde, der udføres på vægten gennem hele processen. Bemærk, at den oprindelige kinetiske energi af vægten er nul, fordi den har nulhastighed. Lad os nu beregne hastigheden ved at anvende forholdet mellem nettoarbejde og ændringen i kinetisk energi.