Die Grundlagen: KNN für Klassifikation und Regression

Datenwissenschaft von Grund auf

Kurse in Datenwissenschaft oder angewandter Statistik beginnen normalerweise mit linearen Modellen, aber auf diese Weise ist K-nearest Neighbors konzeptionell wahrscheinlich das einfachste weit verbreitete Modell. KNN-Modelle sind wirklich nur technische Implementierungen einer gemeinsamen Intuition, dass Dinge, die ähnliche Merkmale aufweisen, in der Regel ähnlich sind. Dies ist kaum ein tiefer Einblick, aber diese praktischen Implementierungen können extrem leistungsfähig sein und, was für jemanden, der sich einem unbekannten Datensatz nähert, von entscheidender Bedeutung ist, Nichtlinearitäten ohne komplizierte Datenentwicklung oder Modelleinrichtung verarbeiten.

Was

Betrachten wir als anschauliches Beispiel den einfachsten Fall der Verwendung eines KNN-Modells als Klassifikator. Angenommen, Sie haben Datenpunkte, die in eine von drei Klassen fallen. Ein zweidimensionales Beispiel kann so aussehen:

Sie können wahrscheinlich ziemlich deutlich sehen, dass die verschiedenen Klassen zusammen gruppiert sind — die obere linke Ecke der Diagramme scheint zur orangefarbenen Klasse zu gehören, der rechte / mittlere Abschnitt zur blauen Klasse. Wenn Sie die Koordinaten eines neuen Punktes irgendwo in der Grafik erhalten und gefragt würden, zu welcher Klasse er wahrscheinlich gehören würde, wäre die Antwort meistens ziemlich klar. Jeder Punkt in der oberen linken Ecke des Diagramms ist wahrscheinlich orange usw.

Etwas unsicherer wird die Aufgabe jedoch zwischen den Klassen, wo wir uns auf eine Entscheidungsgrenze festlegen müssen. Betrachten Sie den neuen Punkt, der unten in Rot hinzugefügt wurde:

Sollte dieser neue Punkt als orange oder blau eingestuft werden? Der Punkt scheint zwischen den beiden Clustern zu liegen. Ihre erste Intuition könnte darin bestehen, den Cluster auszuwählen, der näher am neuen Punkt liegt. Dies wäre der Ansatz des nächsten Nachbarn, und obwohl er konzeptionell einfach ist, liefert er häufig ziemlich vernünftige Vorhersagen. Welcher zuvor identifizierte Punkt ist der neue Punkt am nächsten? Es ist vielleicht nicht offensichtlich, nur die Grafik zu betrachten, was die Antwort ist, aber es ist einfach für den Computer, die Punkte durchzugehen und uns eine Antwort zu geben:

Sieht es so aus, als ob der nächste Punkt in der blauen Kategorie liegt, also ist unser neuer Punkt wahrscheinlich auch. Dies ist die Methode des nächsten Nachbarn.

An dieser Stelle fragen Sie sich vielleicht, wofür das ‚k‘ in k-nearest-neighbors ist. K ist die Anzahl der nahe gelegenen Punkte, die das Modell bei der Bewertung eines neuen Punktes betrachtet. In unserem einfachsten Beispiel für den nächsten Nachbarn war dieser Wert für k einfach 1 – wir haben uns den nächsten Nachbarn angesehen und das war’s. Sie hätten jedoch die nächsten 2 oder 3 Punkte betrachten können. Warum ist das wichtig und warum sollte jemand k auf eine höhere Zahl setzen? Zum einen könnten die Grenzen zwischen den Klassen auf eine Weise nebeneinander stoßen, die es weniger offensichtlich macht, dass der nächste Punkt uns die richtige Klassifizierung gibt. Betrachten Sie die blauen und grünen Regionen in unserem Beispiel. In der Tat, lassen Sie uns auf sie zoomen:

zoomen, stellen Sie fest, dass die Gesamtregionen zwar deutlich genug erscheinen, ihre Grenzen jedoch ein wenig miteinander verflochten zu sein scheinen. Dies ist ein gemeinsames Merkmal von Datensätzen mit ein wenig Rauschen. Wenn dies der Fall ist, wird es schwieriger, Dinge in den Grenzbereichen zu klassifizieren. Betrachten Sie diesen neuen Punkt:

Einerseits sieht es visuell definitiv so aus, als wäre der nächstgelegene zuvor identifizierte Punkt blau, was unser Computer für uns leicht bestätigen kann:

Andererseits scheint dieser nächste blaue Punkt selbst ein Ausreißer zu sein, weit weg vom Zentrum der blauen Region und irgendwie von grünen Punkten umgeben. Und dieser neue Punkt liegt sogar außerhalb dieses blauen Punktes! Was wäre, wenn wir die drei Punkte betrachten würden, die dem neuen roten Punkt am nächsten liegen?

Oder sogar die nächsten fünf Punkte zum neuen Punkt?

Jetzt scheint es, dass unser neuer Punkt in einer grünen Nachbarschaft ist! Es hatte zufällig einen nahe gelegenen blauen Punkt, aber das Übergewicht oder die nahe gelegenen Punkte sind grün. In diesem Fall wäre es vielleicht sinnvoll, einen höheren Wert für k festzulegen, eine Handvoll nahegelegener Punkte zu betrachten und sie irgendwie über die Vorhersage für den neuen Punkt abstimmen zu lassen.

Das dargestellte Problem ist zu passend. Wenn k auf eins gesetzt ist, ist die Grenze, zwischen der Regionen vom Algorithmus als blau und grün identifiziert werden, holprig, sie schlängelt sich mit jedem einzelnen Punkt hin und her. Der rote Punkt sieht aus wie in der blauen Region:

hervorgehoben sind und k auf 5 bringen, glättet jedoch die Entscheidungsgrenze, wenn die verschiedenen nahe gelegenen Punkte abstimmen. Der rote Punkt scheint jetzt fest in der grünen Nachbarschaft zu liegen:

Der Kompromiss mit höheren Werten von k ist der Verlust der Granularität in der Entscheidungsgrenze. Wenn Sie k sehr hoch setzen, erhalten Sie in der Regel glatte Grenzen, aber die realen Grenzen, die Sie modellieren möchten, sind möglicherweise nicht perfekt glatt.

Praktisch gesehen können wir die gleiche Art von Ansatz für Regressionen verwenden, bei denen wir eher einen individuellen Wert als eine Klassifizierung wünschen. Betrachten Sie die folgende Regression unten:

Die Daten wurden zufällig generiert, aber linear generiert, sodass ein lineares Regressionsmodell natürlich gut zu diesen Daten passt. Ich möchte jedoch darauf hinweisen, dass Sie die Ergebnisse der linearen Methode mit einem K-nearest Neighbors-Ansatz konzeptionell einfacher approximieren können. Unsere ‚Regression‘ ist in diesem Fall keine einzelne Formel, wie es uns ein OLS-Modell geben würde, sondern ein am besten vorhergesagter Ausgabewert für eine bestimmte Eingabe. Betrachten Sie den Wert von -.75 auf der x-Achse, die ich mit einer vertikalen Linie markiert habe:

Ohne Gleichungen zu lösen, können wir zu einer vernünftigen Annäherung an die Ausgabe kommen, indem wir nur die nahe gelegenen Punkte berücksichtigen:

Es macht Sinn, dass der vorhergesagte Wert in der Nähe dieser Punkte liegen sollte, nicht viel niedriger oder höher. Vielleicht wäre eine gute Vorhersage der Durchschnitt dieser Punkte:

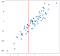
Sie können sich vorstellen, dies für alle möglichen Eingabewerte zu tun und überall Vorhersagen zu treffen:

Wenn wir all diese Vorhersagen mit einer Linie verbinden, erhalten wir unsere Regression:

In diesem Fall sind die Ergebnisse keine klare Linie, aber sie zeichnen die Steigung der Daten einigermaßen gut nach. Dies mag nicht besonders beeindruckend erscheinen, aber ein Vorteil der Einfachheit dieser Implementierung ist, dass sie Nichtlinearität gut handhabt. Betrachten Sie diese neue Sammlung von Punkten:

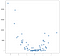
Diese Punkte wurden durch einfaches Quadrieren der Werte aus dem vorherigen Beispiel generiert, aber angenommen, Sie sind in freier Wildbahn auf einen solchen Datensatz gestoßen. Es ist offensichtlich nicht linear in der Natur und während ein Modell im OLS-Stil diese Art von Daten problemlos verarbeiten kann, erfordert es die Verwendung von nichtlinearen oder Interaktionsbegriffen, was bedeutet, dass der Datenwissenschaftler einige Entscheidungen darüber treffen muss, welche Art von Daten-Engineering durchgeführt werden soll. Der KNN-Ansatz erfordert keine weiteren Entscheidungen — derselbe Code, den ich im linearen Beispiel verwendet habe, kann vollständig für die neuen Daten wiederverwendet werden, um einen praktikablen Satz von Vorhersagen zu erhalten:

Wie bei den Klassifikatorbeispielen hilft uns das Festlegen eines höheren Werts k, eine Überanpassung zu vermeiden, obwohl Sie möglicherweise an der Marge an Vorhersagekraft verlieren, insbesondere an den Rändern Ihres Datensatzes. Betrachten Sie den ersten Beispieldatensatz mit Vorhersagen, die mit k auf eins gesetzt wurden, dh einem Ansatz für den nächsten Nachbarn:

Unsere Vorhersagen springen unregelmäßig herum, wenn das Modell von einem Punkt im Datensatz zum nächsten springt. Im Gegensatz dazu führt die Einstellung von k auf zehn, so dass zehn Gesamtpunkte zur Vorhersage gemittelt werden, zu einer viel ruhigeren Fahrt:

Im Allgemeinen sieht das besser aus, aber Sie können etwas von einem Problem an den Rändern der Daten sehen. Da unser Modell so viele Punkte für eine bestimmte Vorhersage berücksichtigt, werden unsere Vorhersagen schlechter, wenn wir uns einer der Kanten unserer Stichprobe nähern. Wir können dieses Problem etwas angehen, indem wir unsere Vorhersagen auf die näheren Punkte gewichten, obwohl dies mit eigenen Kompromissen verbunden ist.

Wie

Beim Einrichten eines KNN-Modells müssen nur wenige Parameter ausgewählt werden, um die Leistung zu verbessern.

K: die Anzahl der Nachbarn: Wie bereits erwähnt, wird die Erhöhung von K dazu neigen, Entscheidungsgrenzen zu glätten und eine Überanpassung auf Kosten einer gewissen Auflösung zu vermeiden. Es gibt keinen einzelnen Wert von k , der für jeden einzelnen Datensatz funktioniert. Für Klassifikationsmodelle, insbesondere wenn es nur zwei Klassen gibt, wird normalerweise eine ungerade Zahl für k . Dies ist so, dass der Algorithmus niemals auf ein Unentschieden stößt: zB betrachtet er die nächsten vier Punkte und stellt fest, dass zwei von ihnen in der blauen Kategorie und zwei in der roten Kategorie sind.

Entfernung metrisch: Wie sich herausstellt, gibt es verschiedene Möglichkeiten zu messen, wie nahe zwei Punkte beieinander liegen, und die Unterschiede zwischen diesen Methoden können in höheren Dimensionen signifikant werden. Am häufigsten wird die euklidische Entfernung verwendet, die Standardsortierung, die Sie möglicherweise in der Mittelschule mit dem Satz des Pythagoras gelernt haben. Eine weitere Metrik ist die sogenannte Manhattan-Entfernung, die die Entfernung in jeder Himmelsrichtung und nicht entlang der Diagonale misst (als ob Sie von einer Straßenkreuzung in Manhattan zur nächsten gehen würden und dem Straßenraster folgen müssten, anstatt die kürzeste Luftlinie zu nehmen). Im Allgemeinen sind dies tatsächlich beide Formen der sogenannten Minkowski-Distanz, deren Formel lautet:

Wenn p auf 1 gesetzt ist, ist diese Formel dieselbe wie die Manhattan-Entfernung und wenn sie auf zwei gesetzt ist, die euklidische Entfernung.

Gewichtungen: Eine Möglichkeit, sowohl das Problem eines möglichen Gleichstands bei der Abstimmung des Algorithmus über eine Klasse als auch das Problem, bei dem sich unsere Regressionsvorhersagen an den Rändern des Datensatzes verschlechtert haben, zu lösen, besteht darin, eine Gewichtung einzuführen. Bei Gewichten zählen die nahen Punkte mehr als die weiter entfernten Punkte. Der Algorithmus betrachtet weiterhin alle nächsten Nachbarn, aber die engeren Nachbarn haben mehr Stimmen als die weiter entfernten. Dies ist keine perfekte Lösung und birgt die Möglichkeit einer erneuten Überanpassung. Betrachten Sie unser Regressionsbeispiel, diesmal mit Gewichten:

Unsere Vorhersagen gehen jetzt direkt an den Rand des Datensatzes, aber Sie können sehen, dass unsere Vorhersagen jetzt viel näher an den einzelnen Punkten schwingen. Die gewichtete Methode funktioniert ziemlich gut, wenn Sie sich zwischen Punkten befinden, aber wenn Sie einem bestimmten Punkt immer näher kommen, hat der Wert dieses Punktes immer mehr Einfluss auf die Vorhersage des Algorithmus. Wenn Sie einem Punkt nahe genug kommen, ist es fast so, als würden Sie k auf eins setzen, da dieser Punkt so viel Einfluss hat.

Skalieren / Normalisieren: Ein letzter, aber entscheidend wichtiger Punkt ist, dass KNN-Modelle abgeworfen werden können, wenn verschiedene Merkmalsvariablen sehr unterschiedliche Skalen haben. Stellen Sie sich ein Modell vor, das beispielsweise versucht, den Verkaufspreis eines Hauses auf dem Markt anhand von Merkmalen wie der Anzahl der Schlafzimmer und der Gesamtfläche des Hauses usw. vorherzusagen. Es gibt mehr Varianz in der Anzahl der Quadratmeter in einem Haus als in der Anzahl der Schlafzimmer. Typischerweise haben Häuser nur eine kleine Handvoll Schlafzimmer, und nicht einmal das größte Herrenhaus wird Dutzende oder Hunderte von Schlafzimmern haben. Quadratfuß hingegen sind relativ klein, so dass Häuser von etwa 1.000 Quadratmetern auf der kleinen Seite bis zu Zehntausenden von Quadratfuß auf der großen Seite reichen können.

Betrachten Sie den Vergleich zwischen einem 2.000 Quadratmeter großen Haus mit 2 Schlafzimmern und einem 2.010 Quadratmeter großen Haus mit zwei Schlafzimmern — 10 qm. füße machen kaum einen Unterschied. Im Gegensatz dazu ist ein 2.000 Quadratmeter großes Haus mit drei Schlafzimmern sehr unterschiedlich und stellt ein sehr anderes und möglicherweise beengteres Layout dar. Ein naiver Computer hätte jedoch nicht den Kontext, um das zu verstehen. Es würde sagen, dass das 3-Schlafzimmer nur eine Einheit vom 2-Schlafzimmer entfernt ist, während die 2,010-Fußzeile zehn von der 2,000-Fußzeile entfernt ist. Um dies zu vermeiden, sollten Feature-Daten vor der Implementierung eines KNN-Modells skaliert werden.

Stärken und Schwächen

KNN-Modelle sind einfach zu implementieren und gehen gut mit Nichtlinearitäten um. Auch die Anpassung des Modells geht tendenziell schnell: Der Computer muss schließlich keine bestimmten Parameter oder Werte berechnen. Der Nachteil hierbei ist, dass das Modell zwar schnell eingerichtet, aber langsamer vorherzusagen ist, da es zur Vorhersage eines Ergebnisses für einen neuen Wert alle Punkte in seinem Trainingssatz durchsuchen muss, um die nächstgelegenen zu finden. Für große Datensätze kann KNN daher eine relativ langsame Methode im Vergleich zu anderen Regressionen sein, deren Anpassung möglicherweise länger dauert, deren Vorhersagen dann jedoch mit relativ einfachen Berechnungen getroffen werden.

Ein weiteres Problem mit einem KNN-Modell ist, dass es an Interpretierbarkeit mangelt. Eine lineare OLS-Regression hat eindeutig interpretierbare Koeffizienten, die selbst einen Hinweis auf die Effektgröße eines bestimmten Merkmals geben können (obwohl bei der Zuweisung von Kausalität Vorsicht geboten ist). Die Frage, welche Funktionen den größten Effekt haben, ist für ein KNN-Modell jedoch nicht wirklich sinnvoll. Teilweise aus diesem Grund können KNN-Modelle auch nicht wirklich für die Merkmalsauswahl verwendet werden, so wie eine lineare Regression mit einem zusätzlichen Kostenfunktionsterm wie Ridge oder Lasso oder die Art und Weise, wie ein Entscheidungsbaum implizit auswählt, welche Merkmale am wertvollsten erscheinen.