Stationarität bedeutet, dass sich die statistischen Eigenschaften einer Zeitreihe, dh Mittelwert, Varianz und Kovarianz, im Laufe der Zeit nicht ändern. Viele statistische Modelle erfordern, dass die Reihen stationär sind, um effektive und präzise Vorhersagen zu treffen.
Zwei statistische Tests würden verwendet, um die Stationarität einer Zeitreihe zu überprüfen – der Dickey Fuller („ADF“) -Test und der Kwiatkowski-Phillips-Schmidt-Shin („KPSS“) -Test. Es ist auch ein Verfahren zur Umwandlung einer nichtstationären Zeitreihe in eine stationäre Zeitreihe anzuwenden.
Diese erste Zelle importiert Standardpakete und legt fest, dass Diagramme inline angezeigt werden.
:
%matplotlib inlineimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport statsmodels.api as sm
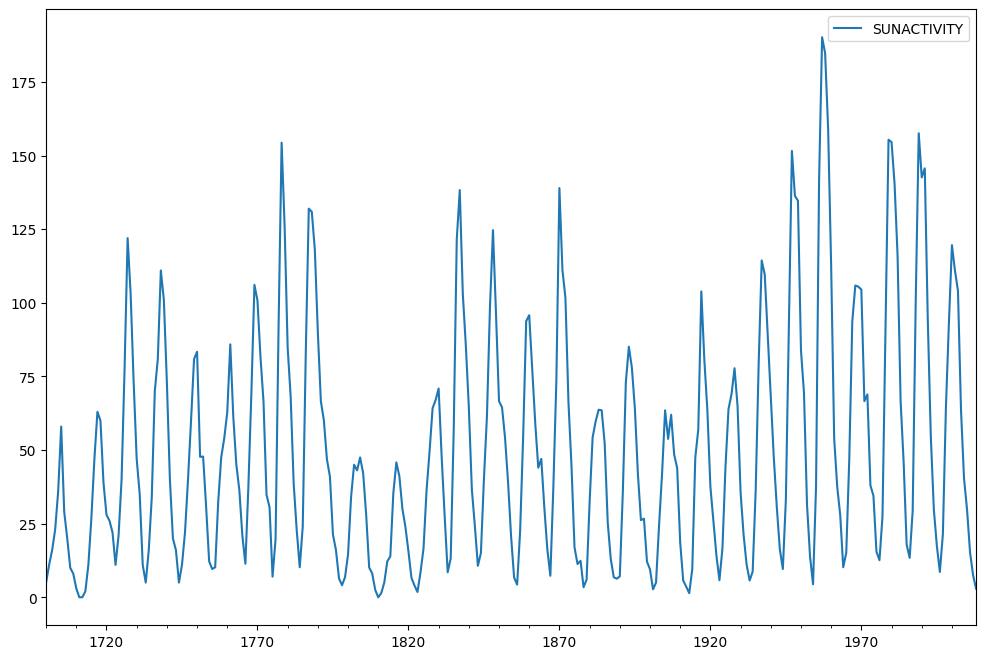
Sonnenflecken Datensatz verwendet wird. Es enthält jährliche (1700-2008) Daten zu Sonnenflecken aus dem National Geophysical Data Center.
:
sunspots = sm.datasets.sunspots.load_pandas().data
Einige Vorverarbeitungen werden an den Daten durchgeführt. Die Spalte „JAHR“ wird beim Erstellen des Index verwendet.
:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))del sunspots
Die Daten werden jetzt geplottet.
:
sunspots.plot(figsize=(12,8))
:
<AxesSubplot:>
ADF-Test¶
Der ADF-Test wird verwendet, um das Vorhandensein von Einheitenwurzeln in der Serie zu bestimmen, und hilft daher zu verstehen, ob die Serie stationär ist oder nicht. Die Null- und Alternativhypothese dieses Tests lautet:
Nullhypothese: Die Reihe hat eine Einheitswurzel.
Alternative Hypothese: Die Reihe hat keine Einheitenwurzel.
Wenn die Nullhypothese in nicht abgelehnt wurde, kann dieser Test den Nachweis erbringen, dass die Reihe nicht stationär ist.
Es wird eine Funktion erstellt, um den ADF-Test an einer Zeitreihe durchzuführen.
:
from statsmodels.tsa.stattools import adfullerdef adf_test(timeseries): print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC') dfoutput = pd.Series(dftest, index=) for key,value in dftest.items(): dfoutput = value print (dfoutput)
KPSS-Test¶
KPSS ist ein weiterer Test zur Überprüfung der Stationarität einer Zeitreihe. Die Null- und Alternativhypothese für den KPSS-Test stehen der des ADF-Tests gegenüber.
Nullhypothese: Der Prozess ist nicht stationär.
Alternativhypothese: Die Reihe hat eine Einheitswurzel (Reihe ist nicht stationär).
Es wird eine Funktion erstellt, um den KPSS-Test an einer Zeitreihe durchzuführen.
:
from statsmodels.tsa.stattools import kpssdef kpss_test(timeseries): print ('Results of KPSS Test:') kpsstest = kpss(timeseries, regression='c', nlags="auto") kpss_output = pd.Series(kpsstest, index=) for key,value in kpsstest.items(): kpss_output = value print (kpss_output)
Die ADF-Tests liefern die folgenden Ergebnisse – Teststatistik, p-Wert und der kritische Wert in 1% -, 5% – und 10% -Konfidenzintervallen.
Der ADF-Test wird nun auf die Daten angewendet.
:
adf_test(sunspots)
Results of Dickey-Fuller Test:Test Statistic -2.837781p-value 0.053076#Lags Used 8.000000Number of Observations Used 300.000000Critical Value (1%) -3.452337Critical Value (5%) -2.871223Critical Value (10%) -2.571929dtype: float64
Basierend auf dem Signifikanzniveau von 0,05 und dem p-Wert des ADF-Tests kann die Nullhypothese nicht abgelehnt werden. Daher ist die Serie nicht stationär.
Die KPSS-Tests liefern die folgenden Ergebnisse – Teststatistik, p-Wert und der kritische Wert in 1% -, 5% – und 10% -Konfidenzintervallen.
Der KPSS-Test wird nun auf die Daten angewendet.
:
kpss_test(sunspots)
Results of KPSS Test:Test Statistic 0.669866p-value 0.016285Lags Used 7.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
Basierend auf dem Signifikanzniveau von 0,05 und dem p-Wert des KPSS-Tests gibt es Hinweise darauf, dass die Nullhypothese zugunsten der Alternative abgelehnt wird. Daher ist die Serie gemäß dem KPSS-Test nicht stationär.
Es ist immer besser, beide Tests anzuwenden, damit sichergestellt werden kann, dass die Serie wirklich stationär ist. Mögliche Ergebnisse der Anwendung dieser stationären Tests sind wie folgt:
Hier, aufgrund der unterschied in die ergebnisse von ADF test und KPSS test, es kann gefolgert werden, dass die serie ist trend stationäre und nicht strenge stationäre. Die Serie kann durch Differenzierung oder durch Modellanpassung beeinträchtigt werden.
Detrending by Differencing¶
Es ist eine der einfachsten Methoden zum Detrending einer Zeitreihe. Es wird eine neue Reihe erstellt, bei der der Wert im aktuellen Zeitschritt als Differenz zwischen der ursprünglichen Beobachtung und der Beobachtung im vorherigen Zeitschritt berechnet wird.
Die Differenzierung wird auf die Daten angewendet und das Ergebnis wird aufgetragen.
:
sunspots = sunspots - sunspots.shift(1)sunspots.dropna().plot(figsize=(12,8))
:
<AxesSubplot:>
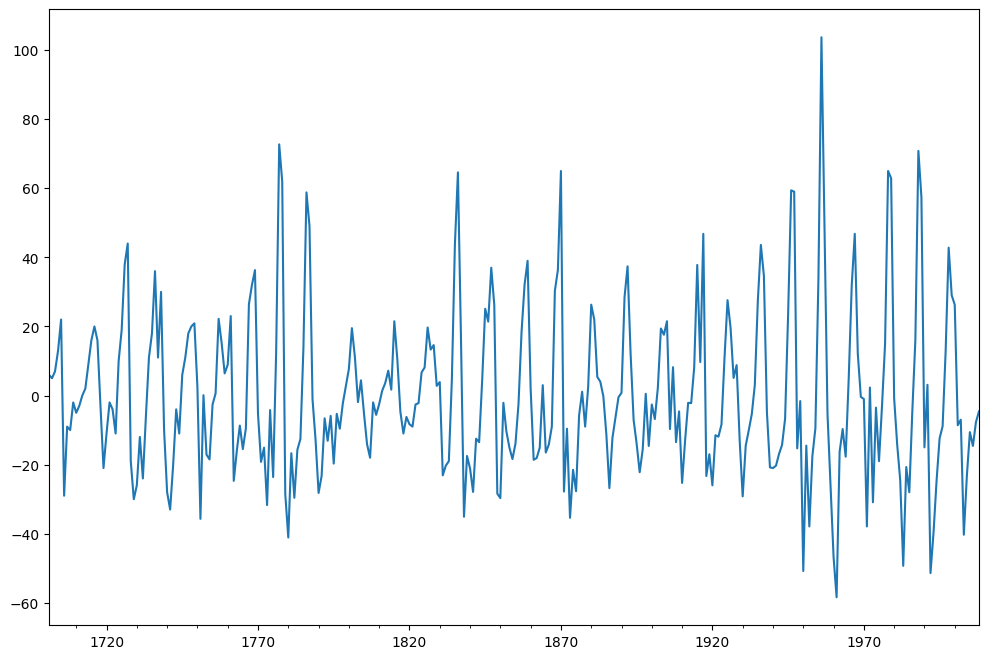
Der ADF-Test wird nun auf diese Detrended-Werte angewendet und die Stationarität wird überprüft.
:
adf_test(sunspots.dropna())
Results of Dickey-Fuller Test:Test Statistic -1.486166e+01p-value 1.715552e-27#Lags Used 7.000000e+00Number of Observations Used 3.000000e+02Critical Value (1%) -3.452337e+00Critical Value (5%) -2.871223e+00Critical Value (10%) -2.571929e+00dtype: float64
Basierend auf dem p-Wert des ADF-Tests gibt es Hinweise darauf, dass die Nullhypothese zugunsten der Alternative abgelehnt wird. Daher ist die Serie jetzt streng stationär.
KPSS-Test wird nun auf diese Detrended-Werte angewendet und die Stationarität wird überprüft.
:
kpss_test(sunspots.dropna())
Results of KPSS Test:Test Statistic 0.021193p-value 0.100000Lags Used 0.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/stattools.py:1911: InterpolationWarning: The test statistic is outside of the range of p-values available in thelook-up table. The actual p-value is greater than the p-value returned. warn_msg.format(direction="greater"), InterpolationWarning
Basierend auf dem p-Wert des KPSS-Tests kann die Nullhypothese nicht abgelehnt werden. Daher ist die Serie stationär.
Schlussfolgerung¶
Es werden zwei Tests zur Überprüfung der Stationarität einer Zeitreihe verwendet, nämlich der ADF-Test und der KPSS-Test. Detrending wird durch Differenzierung durchgeführt. Trend stationäre Zeitreihen werden in strikte stationäre Zeitreihen umgewandelt. Das erforderliche Prognosemodell kann nun auf stationäre Zeitreihendaten angewendet werden.