Kinetische Energie ist die Energie der Bewegung. Ein Ausdruck für kinetische Energie wird abgeleitet, indem der Fall eines Objekts betrachtet wird, das auf eine relative Höhe angehoben wird (also an diesem Objekt gearbeitet wird) und dann fallen gelassen wird.
Schlüsselbegriffe
o Kinetische Energie
Ziele
o Leiten Sie einen Ausdruck für kinetische Energie aus dem physikalischen Konzept der Arbeit ab
o Verstehen Sie das Verhältnis von Arbeit und kinetischer Energie
o Berechnen Sie die kinetische Energie verschiedener Objekte
Fangen wir an!
In Bezug auf Arbeit und kinetische Energie
In gewissem Sinne ist Arbeit die Menge an Energie, die in eine Aufgabe (oder vielleicht „in das Objekt“) gesteckt wird. Stellen Sie sich zum Beispiel vor, wir nehmen ein Objekt vom Boden auf und heben es auf eine bestimmte Höhe an; wir haben eine gewisse Arbeit an diesem Objekt geleistet. Wenn wir es jedoch loslassen, beschleunigt es sich, als ob die Arbeit, die wir beim Anheben des Objekts geleistet haben, in Bewegung umgewandelt wird. Durch dieses Beispiel können wir eine Definition für kinetische Energie ableiten, die Bewegungsenergie ist. Diese Definition hängt, wie wir sehen werden, eng damit zusammen, wie wir Arbeit definiert haben.
Betrachten wir zunächst ein Objekt: einen Ball der Masse m. Wir heben den Ball von einem Tisch auf und heben ihn ein Stück h über diesen Tisch, wie unten gezeigt. Wir haben daher eine Arbeitsmenge W = mgh geleistet (dieses Ergebnis ist das Produkt der Größe des Verschiebungsvektors (h) und der aufgebrachten Kraft (mg) – die entsprechenden Vektoren sind parallel).
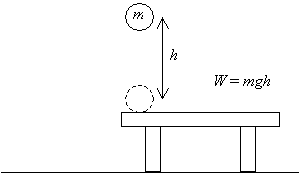
Wenn wir nun diesen Ball loslassen und ihn von der Höhe h über dem Tisch fallen lassen, hat er, sobald er auf seine ursprüngliche Höhe (das Niveau des Tisches) zurückgekehrt ist, eine bestimmte Geschwindigkeit v, die sich aus der Beschleunigung aufgrund der Schwerkraft ergibt.
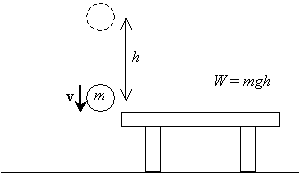
Wir wollen diese Geschwindigkeit berechnen (oder Geschwindigkeit, technisch – wir können gelegentlich den Begriff Geschwindigkeit für Geschwindigkeit ersetzen, aber immer bewusst sein, dass Geschwindigkeit tatsächlich ein Vektor ist und Geschwindigkeit die Größe der Geschwindigkeit ist). Wir wissen, dass die Beschleunigung aufgrund der Schwerkraft konstant ist und dass die Anfangsgeschwindigkeit des Balls Null ist (er ist stationär, bevor er freigegeben wird). Wir nehmen an, dass die Anfangshöhe des Balls h ist und dass seine endgültige Höhe Null ist (die Höhe des Tisches). Um die Geschwindigkeit durch Ableitung der entsprechenden Formeln zu berechnen, benötigen wir die Verwendung der elementaren Integralrechnung. (Wenn Sie ein fortgeschrittener Student sind oder eine zusätzliche Herausforderung suchen, können Sie versuchen, diese Formeln unter den oben genannten Bedingungen selbst abzuleiten. Beachten Sie einfach, dass die Geschwindigkeit v der Kugel die zeitliche Änderungsrate ihrer Position x als Funktion der Zeit t ![]() und die Beschleunigung a die zeitliche Änderungsrate der Geschwindigkeit
und die Beschleunigung a die zeitliche Änderungsrate der Geschwindigkeit ![]() ist.)
ist.)
![]()
![]()
Diese Formeln drücken die Geschwindigkeit als Funktion der Zeit, v (t), und die Position (Höhe) als Funktion der Zeit, x(t), in Bezug auf die Beschleunigung a, Höhe h und Zeit t. Wir wissen, dass a = –g , da der Ball nur durch die Schwerkraft beschleunigt wird und diese Beschleunigung nach unten ist (daher das negative Vorzeichen). Die Endposition des Balls ist null Meter oder x (t) = 0. Berechnen wir t, die Zeit zwischen der Freigabe des Balls und seiner Ankunft auf der Ebene des Tisches.
![]()
![]()
![]()
Berechnen wir nun die Geschwindigkeit des Balls zu diesem Zeitpunkt.
![]()
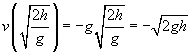
Vergleichen wir nun dieses Ergebnis mit der ursprünglich am Objekt geleisteten Arbeit: W = mgh. Beachten Sie, wie nahe diese beiden Ausdrücke in der Form sind; Tatsächlich ist der einzige Faktor, der in der Geschwindigkeit fehlt, die Masse der Kugel, m. Wenn wir die Geschwindigkeit quadrieren, mit m multiplizieren und dann durch 2 dividieren, hätten wir tatsächlich den gleichen Ausdruck wie das Werk!
![]()
So können wir in gewissem Sinne sehen, wie die Definition der kinetischen Energie abgeleitet werden kann. Die kinetische Energie K eines Objekts ist dann ein Skalar, der wie folgt definiert ist, wobei m die Masse des Objekts und v seine Geschwindigkeit ist:
![]()
Wie sich herausstellt, ist die kinetische Energie die Arbeit, die an einem Objekt durch die Nettokraft auf dieses Objekt geleistet wird. Obwohl also eine Frau eine bestimmte Menge an Arbeit an einem Objekt ausführen kann, indem sie es von einer Höhe zur anderen hebt, ist die Nettokraft auf dieses Objekt Null (die Frau wendet eine Kraft an, die in Richtung der Schwerkraft gleich, aber entgegengesetzt ist). Somit gibt es keine Änderung der kinetischen Energie. Wenn dieses Objekt jedoch losgelassen und fallen gelassen wird, gewinnt es kinetische Energie, da die Nettokraft auf es einfach die der Schwerkraft ist (eine einzige Kraft). Um die Beziehung zwischen kinetischer Energie und Arbeit zu verstehen, müssen wir unseren Arbeitsbegriff etwas verfeinern. Wenn wir die Arbeit W als die Gesamtarbeit definieren, die von allen Kräften am Objekt geleistet wird (mit anderen Worten, die Arbeit, die von der Nettokraft am Objekt geleistet wird), dann gilt die folgende Beziehung zwischen der Arbeit W und den anfänglichen und endgültigen kinetischen Energien (Ki und Kf).
![]() wobei
wobei ![]()
Somit ist die an einem Objekt geleistete Nettoarbeit gleich der Änderung der kinetischen Energie dieses Objekts (ΔK). Die folgenden Übungsprobleme bieten Ihnen die Möglichkeit, Ihr Verständnis der Konzepte von Arbeit und kinetischer Energie zu testen und anzuwenden.
Übungsproblem: Ein Projektil mit einer Masse von 1 Kilogramm bewegt sich mit 5 Metern pro Sekunde. Welche Geschwindigkeit muss ein 0,1 Kilogramm schweres Projektil zurücklegen, um die gleiche kinetische Energie zu erreichen?
Lösung: Berechnen wir zunächst die kinetische Energie des massereicheren (1 kilogramm) Projektils.
![]()
Wir können nun die Geschwindigkeit des weniger massereichen Objekts so berechnen, dass es dieselbe kinetische Energie hat, K.
![]()
![]()
![]()
Übungsproblem: Ein Mann hebt ein 15 Kilogramm schweres Gewicht auf eine Höhe von zwei Metern vom Boden, bevor er es fallen lässt. In dem Moment, bevor das Gewicht den Boden berührt, wie schnell ist es?
Lösung: Zeichnen wir ein Diagramm, das die Kräfte zeigt, die auf das Objekt wirken, wenn es angehoben wird und fällt; Diese Kräfte umfassen die Schwerkraft (Fg) und die Aufwärtskraft, die der Mann ausübt (Fu).
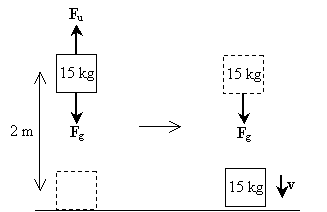
Beachten Sie, dass der erste Schritt des Prozesses (Heben des Gewichts) keine Nettokraft beinhaltet, die auf das Objekt einwirkt – die Kraft aufgrund der Schwerkraft wird durch die Kraft ausgeglichen, die der Mann beim Heben des Gewichts ausübt. Im zweiten Schritt erfährt das Gewicht jedoch nur die Schwerkraft. Die Nettokraft ist in diesem Fall also nach unten gerichtet. Als solches ist die Geschwindigkeit des Objekts auch in der Abwärtsrichtung. Die Arbeit, die auf dem Gewicht infolge der Schwerkraft getan wird, ist einfach mgh; dieses ist auch die Gesamtarbeit, die auf dem Gewicht während des Prozesses getan wird. Beachten Sie, dass die anfängliche kinetische Energie des Gewichts Null ist, da es eine Geschwindigkeit von Null hat. Berechnen wir nun die Geschwindigkeit, indem wir die Beziehung zwischen der Nettoarbeit und der Änderung der kinetischen Energie anwenden.