Wissensstruktur

Auszug aus einer Broschüre, die einen Workshop für Naturwissenschaftslehrer an Gymnasien begleitet.

von Robert J. Dufresne, William J. Leonard und William J. Gerace

Unsere Gruppe bei UMass hat ein kognitives Modell entwickelt, das uns hilft, die Unterschiede in der Art und Weise darzustellen, wie Experten und Anfänger Inhaltswissen speichern und verwenden. Das Modell hilft uns auch, bestimmte Bereiche anzusprechen, auf die sich Anfänger konzentrieren müssen, um bessere Problemlöser zu werden. Das Modell ist jedoch nur eine Darstellung der Wissensstruktur und entwickelt sich ständig weiter. Daher darf es nicht zu wörtlich genommen werden. Seine Nützlichkeit beruht auf seiner Fähigkeit, die Denkweise von Experten und Anfängern konkret zum Ausdruck zu bringen, auch wenn sie unvollkommen ist. Das Modell hilft uns zu diskutieren:

1. die Speicherung von domänenspezifischem Wissen;
2. experten- und anfängerähnliches Problemlösungsverhalten;
3. die hierarchische Struktur des Wissensspeichers eines Experten;
4. Missverständnisse;
5. die Auswirkungen zielfreier und zielgerichteter Fragen; und
6. der Metakommunikationsprozess.

In diesem Workshop — und in unserem Ansatz zur Physik im Allgemeinen — gibt es 3 Grundthemen:

1. Bestimmte Arten von Wissen und Wissensstrukturen sind für eine kompetente Problemlösung erforderlich. Ein Großteil dieses Wissens ist konzeptioneller Natur, im Gegensatz zu operativen oder prozeduralen, und mächtige Wissensstrukturen beinhalten notwendigerweise konzeptionelle Elemente. Das Vorhandensein konzeptioneller Elemente in den Wissensstrukturen ist der Schlüssel zu einem „tieferen Verständnis“ der Physik.
2. Für den Erwerb von konzeptionellem Wissen und den Aufbau nützlicher Wissensstrukturen sind bestimmte Arten kognitiver Prozesse erforderlich.
3. Es ist möglich, Aktivitäten zu entwerfen, die diese wünschenswerten kognitiven Prozesse fördern. In vielen Fällen sind diese Aktivitäten einfach Aktualisierungen der kognitiven Prozesse selbst. (Dieser Punkt wird hoffentlich später klarer werden.)

Wir werden auf jedes dieser Themen eingehen, bevor wir uns auf spezifische Beispiele konzentrieren.

Thema 1: Was müssen Studierende wissen und wie sollte das, was sie wissen, für eine effiziente Problemlösung strukturiert sein?

Wir beginnen mit der Identifizierung einiger der verschiedenen Arten von Wissen, die die Schüler kennen müssen:

• Konzeptionelles Wissen, wie das Konzept des Impulses oder der Energie, oder dass sich die Geschwindigkeit eines Objekts ändert, wenn es beschleunigt wird, oder dass die potentielle Gravitationsenergie eines Objekts abnimmt, wenn es fällt.
• Faktenwissen, wie der Wert der Gravitationskonstante g, der Radius des Mondes oder die Dichte von Eisen.
• Darstellungswissen, z. B. Zeichnen und Verwenden von Diagrammen.
• Strategisches Wissen, z. B. die Fähigkeit, die Anwendbarkeit eines Konzepts zu erkennen, z. B. dass der Impuls erhalten bleibt, wenn keine äußeren Kräfte vorhanden sind, oder dass die Energie erhalten bleibt, wenn keine nicht konservativen Kräfte vorhanden sind.
• Metakognitives Wissen, zum Beispiel das Bewusstsein für zugrunde liegende Annahmen oder dass eine Antwort überprüft werden sollte, indem das Problem auf andere Weise gelöst wird.
• Selbsterkenntnis, z. B. die wahrscheinlichen Fehlerquellen zu kennen oder zu wissen, dass man bei der Lösung von Problemen prozeduraler sein sollte.
• Operatives Wissen, z. B. wie man das Kreuzprodukt oder Punktprodukt zweier Vektoren nimmt oder wie man die Determinante einer Matrix nimmt oder wie man ein Freikörperdiagramm zeichnet.
• Verfahrenstechnisches Wissen, z.B. wann Energieeinsparung (z.B. wenn alle Kräfte konservativ sind), oder wenn ein Koordinatensystem angegeben werden soll (z. B. beim Auffinden potenzieller Energie) oder wenn ein Freikörperdiagramm gezeichnet werden soll (z. B. bei Anwendung der Newtonschen Gesetze).
• Problem-state knowledge, Das sind die Merkmale eines Problems, mit denen entschieden wird, wie es gelöst werden soll. Beispiele sind: zu wissen, dass es keine externen Kräfte in einem bestimmten Problem gibt, oder dass es keine nicht-konservativen Kräfte in dem Problem gibt, oder dass ein Objekt anfänglich in Ruhe ist, oder dass das Objekt auf einer Steigung ist.

Diese Arten von Wissen müssen organisiert und strukturiert werden, um sie bei der Problemlösung effizient nutzen zu können. Um die organisatorischen und strukturellen Aspekte von Wissen zu diskutieren, haben wir es für zweckmäßig befunden, diese Typen grob in drei allgemeine Kategorien einzuteilen. Wir nennen diese drei Gruppen: Konzeptionelles Wissen, operatives und prozedurales Wissen und Problem-State-Wissen. In Fig. 1 werden diese drei allgemeinen Kategorien in einer Darstellung dargestellt, wie Experten Inhaltswissen speichern.

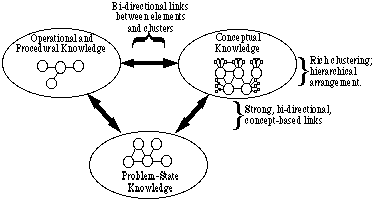Abb. 1: Eine Darstellung der Wissensstruktur eines Experten

Der Experte verfügt über ein reichhaltiges Clustering von Konzepten, in denen jedes Konzept mit vielen anderen Konzepten in Beziehung steht und die Beziehungen zwischen Konzepten klar verstanden werden. Konzepte werden hierarchisch unter Verwendung von Dachkonzepten angeordnet, um sie enger in Beziehung zu setzen. Tatsächlich werden Umbrella-Konzepte verwendet, um Elemente innerhalb jeder der drei Kategorien zu gruppieren. Der Experte verfügt über ein großes Wissen über den Problemzustand, einschließlich vieler Informationen darüber, welche Prinzipien für bestimmte Situationen gelten. Der Experte verfügt auch über einen großen Speicher von Gleichungen, Operationen und Prozeduren (EOPs), auf die schnell zugegriffen werden kann.

Die Verbindungen zwischen jedem Kategorienpaar sind sehr stark: Problemzustände sind stark mit Konzepten und EOPs verbunden, die selbst stark miteinander verbunden sind. Dieselben Umbrella-Konzepte werden verwendet, um Konzepte, Problemzustände und EOPs zu gruppieren. Daher können für jedes bestimmte Problem Konzepte verwendet werden, um die Angemessenheit und Anwendbarkeit von Gleichungen sowie den Nutzen bestimmter Operationen und Verfahren zu bestimmen.

(Man muss hier sehr vorsichtig sein, nicht zu starr im Denken zu sein, denn es ist leicht, sich darüber zu streiten, welche dieser Kategorien verwendet werden sollte, um ein bestimmtes Element des Wissens zu klassifizieren, oder ob es nur in eine Kategorie gehört. Unser Ziel ist es einfach, einen Mechanismus zur Visualisierung der verschiedenen Assoziationsebenen zu haben, die zwischen Elementen auftreten können.)

Wir neigen dazu, den Begriff Linking zu verwenden, um eine gebildete Assoziation zwischen zwei Elementen desselben oder verschiedener Wissenstypen zu bezeichnen, und den Begriff Clustering, um Assoziationen zwischen mehreren Elementen oder Clustern zu bezeichnen. Was diese Art von Diskussion sehr schwierig macht, ist, dass hier eine Art iterativer Prozess stattfindet: Eine sehr starke Verbindung zwischen drei Elementen – einem konzeptionellen Cluster, der Anerkennung der Umstände, die das Konzept anwendbar machen, und den Verfahren, die zur Anwendung des Konzepts erforderlich sind – bildet eine neue Art von Wissenselement, das wir in strategisches Wissen (eine vierte Kategorie) einfügen. Dieses neue Wissenselement wird von einigen als Schema bezeichnet und beinhaltet häufig auch problematisches Wissen. Da das Wissenselement konzeptueller Natur ist, wird es in der konzeptuellen Blase repliziert (dh wiederholt).

Wenn wir uns die konzeptionelle Blase genauer ansehen, sehen wir einige der spezifischen Arten von konzeptionellem Wissen, zum Beispiel Repräsentatives Wissen, strategisches Wissen, Metakognitives Wissen und Wissen über grundlegende Konzepte. Dies ist in Fig. 2. (Andere Arten von konzeptionellem Wissen werden nicht gezeigt.)

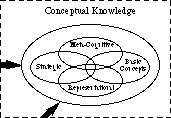Abb. 2: Arten von konzeptionellem Wissen

Wie unterscheidet sich die Wissensstruktur eines Anfängers von der eines Experten? Wie in Fig. 3, anfänger haben in der regel eine schlechte clustering von konzepten. Viele Links sind unangemessen; andere sind nicht vorhanden. Einige der unangemessenen Links sind extrem stark, was zu Missverständnissen führt. Anfänger verwenden im Allgemeinen keine Umbrella-Konzepte, um Elemente zu gruppieren. Sie haben einen kleinen Vorrat an Problemsituationen, in denen Oberflächenmerkmale verwendet werden, um sie zusammenzufassen und zu entscheiden, wie Probleme gelöst werden sollen. Sie sind mit einer relativ großen Anzahl von Gleichungen vertraut, merken sich diese jedoch oft falsch oder müssen sie nachschlagen, um sie verwenden zu können. Ihnen wurden Operationen und Verfahren beigebracht, aber sie beherrschen sie noch nicht. Daher kann nicht gesagt werden, dass sie sie „kennen“.

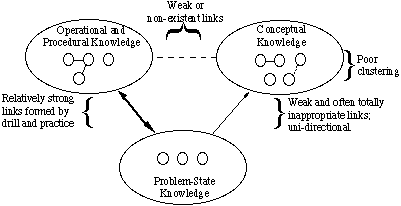Abb. 3: Eine Darstellung der Wissensstruktur des Novizen

Verknüpfungen zwischen Konzepten und EOPs sind schwach oder nicht vorhanden. Verbindungen zwischen Konzepten und Problemsituationen sind ebenfalls schwach. Daher kann ein Anfänger ein Problem nicht analysieren und nicht über die Angemessenheit bestimmter Gleichungen entscheiden. Die Verbindungen zwischen Problemsituationen und EOPs sind relativ stark, aber die Verbindungen basieren hauptsächlich auf den Größen, die die Gleichungen mit den gegebenen und expliziten Unbekannten des Problems gemeinsam haben.

Themenkreis 2: An welchen kognitiven Prozessen müssen sich Studierende beteiligen, um geeignete Wissensstrukturen zu entwickeln?

Um diese Frage zu beantworten, müssen wir zunächst verstehen, wie Experten und Anfänger Probleme unterschiedlich lösen.

Anfänger sind im Allgemeinen erfolglos, wenn sie versuchen, typische Probleme in der Physik zu lösen. Wie löst ein typischer Anfänger ein Problem, indem er das Modell zur Darstellung des Prozesses verwendet? Da die stärksten Verbindungen in der Wissensstruktur des Anfängers zwischen Problemsituationen und Gleichungen bestehen, schlägt das Lesen eines Problems sofort Gleichungen vor, an denen die im Problem explizit angegebenen Größen (bekannt und unbekannt) beteiligt sind. Ohne die Anwendbarkeit dieser Gleichungen zu bestimmen und ohne zu versuchen, an andere Gleichungen zu denken, die die gleichen Größen beinhalten könnten, beginnt der Anfänger normalerweise, die vertrautesten Gleichungen zu manipulieren, bis das Unbekannte gelöst werden kann. Die neueste Gleichung, die im Unterricht behandelt wird, ist am leichtesten zugänglich und am schnellsten abrufbar. Somit sucht und findet der Neuling (wenn „erfolgreich“) nur einen Weg, um ein Problem zu lösen, und stoppt normalerweise, ohne andere Möglichkeiten zu untersuchen und ohne die Problemsituation zu analysieren. Die auf diese Weise gefundenen Gleichungen sind oft unangemessen, da Anfänger häufig keine Konzepte verwenden, um ihre Anwendung zu rechtfertigen. Selbst wenn die Schüler dazu getrieben werden, Konzepte aufzurufen, indem sie Probleme im Voraus analysieren, sind ihre Verbindungen zu EOPs im Allgemeinen zu schwach, um für die Problemlösung nützlich zu sein. Verknüpfungen zwischen Konzepten und Problemsituationen sind auch unidirektional, sodass Analogien nicht besonders nützlich sind: Anfänger können keine Analogien verwenden, um Probleme zu lösen, weil sie nicht erkennen können, welche der Probleme, die sie bereits gelöst haben, konzeptionell denen ähneln, die sie gerade zu lösen versuchen. Stattdessen verwenden Anfänger Oberflächenmerkmale, um „Ähnlichkeit“ herzustellen und versuchen, neue Probleme basierend auf ihrer Ähnlichkeit mit den Oberflächenmerkmalen von Problemen zu lösen, die sie bereits gelöst haben.

Da Experten Probleme und EOPs nach denselben Dachkonzepten klassifizieren, können sie oft direkt von Problemsituationen zu geeigneten Gleichungen, Operationen und / oder Prozeduren übergehen. Da die Verbindungen zwischen verschiedenen Kategorien stark sind, können schwierige Probleme (für die es noch keine direkte Verbindung zwischen Problemzuständen und EOPs gibt) gelöst werden, indem bewusst Konzepte aufgerufen werden, wodurch Problemzustände indirekt mit den entsprechenden EOPS verbunden werden. Da die Verbindungen zwischen Konzepten und Problemsituationen bidirektional sind, sind Analogien ein äußerst nützliches Werkzeug zur Problemlösung für Experten. Schließlich haben Experten in der Regel mehr als einen Ansatz zur Lösung eines bestimmten Problems.

Hier finden Sie eine Zusammenfassung der wichtigsten Unterschiede zwischen Experten und Anfängern:

1. Anfänger haben ein schlechtes Clustering von Konzepten, was oft zu Missverständnissen führt. Experten verfügen über ein reichhaltiges Clustering von Konzepten, Problemsituationen, Gleichungen, Verfahren und Operationen, was zu einer verbesserten Problemlösungsfähigkeit führt.
2. Anfänger haben in der Regel nur einen Weg, ein bestimmtes Problem zu lösen, während Experten oft mehr als einen Weg finden können. Daher kann der Experte versuchen, Inkonsistenzen aufzulösen, wenn sie auftreten, und Antworten überprüfen, während Anfänger nicht wissen, dass Inkonsistenzen bestehen, und ihre Antworten nicht überprüfen können.
3. Anfänger verwenden häufig Gleichungsmanipulation und selten konzeptbasierte Strategien, um eine Antwort zu erhalten. Der Experte schlägt anhand von Konzepten und Analogien verschiedene Lösungsmethoden vor und plant eine Strategie, um die richtige Antwort zu finden.
4. Anfänger bekommen oft nicht die richtige Antwort, und wenn sie die richtige Antwort bekommen, kann es leicht aus dem falschen Grund sein. Wenn der Anfänger aus dem falschen Grund die richtige Antwort erhält, werden Missverständnisse verstärkt und es wird noch schwieriger, sie zu überwinden. Ein Experte erhält normalerweise die richtige Antwort und kann erklären, warum die Antwort richtig ist.

Es gibt eine Vielzahl kognitiver Prozesse, die Anfängern helfen, einen konzeptbasierten Problemlösungsansatz zu entwickeln, den wir in drei Kategorien unterteilen: Analyseprozesse, Argumentationsprozesse und metakognitive Prozesse.

Analyseprozesse

• Problemanalyse, z. B. Erstellung einer Problemdarstellung.
• Konzeptionelle Analyse, z. B. die Verwendung von Konzepten zur Bestimmung des qualitativen Verhaltens physischer Objekte oder zur Bildung einer Strategie.
• Strategische Analyse, z. B. Identifizierung und Rechtfertigung physikalischer Prinzipien, die für eine Problemsituation relevant sind.
• Repräsentationsanalyse, z. B. Untersuchung verschiedener Repräsentationen eines Problems.
• Komplexe konstruktive Analyse, z. B. Zerlegung einer komplexen Situation in einfachere.

Argumentationsprozesse

• Vergleichen und Kontrastieren, z. B. Identifizieren, wie Elemente, Situationen oder Bedingungen ähnlich und / oder unterschiedlich sind.
• Interpretieren, zum Beispiel unter Verwendung der Form eines Diagramms von Position vs. zeit, um die Beschleunigung des Objekts zu schätzen.
• Sonder- und Grenzfälle, d.h. Erkundung extremer und/oder bekannter Bedingungen.
• Prototyp und Gegenbeispiele, z.B. Generierung archetypischer Kategorien.
• Verallgemeinerung, dh Erkennen der hervorstechenden Merkmale eines Umstands oder einer Situation.

Metakognitive Prozesse

• Reflexion, dh selbstgesteuerte Überprüfung von Zweck, Zielen, Auswirkungen von Erfahrungen usw.
• Meta-Kommunikation, die bewusste Teilnahme an der Etablierung und Verfeinerung von Kommunikationslinien mit dem Lehrer und anderen Schülern sowie an der Entscheidung über die Lernziele.
• Selbsteinschätzung, z. B. Bewertung der eigenen Leistung oder Ermittlung von Gründen, aus denen bei der Lösung eines Problems Schwierigkeiten aufgetreten sind.

Diese und andere Prozesse werden durch unsere Lehrmaterialien gefördert. Die spezifischen Arten von Aktivitäten, um dies zu tun, werden im nächsten Abschnitt vorgestellt.

Themenkreis 3: Welche Arten von Lernaktivitäten oder Erfahrungen fördern diese positiven kognitiven Prozesse?

Die folgenden Aktivitäten können von Lehrern verwendet werden, um die kognitiven Prozesse zu stimulieren, die erforderlich sind, um ein konzeptionelles Verständnis der Physik zu entwickeln:

1. Verwenden Sie mehrere Darstellungen. Eine Darstellung kann sprachlich, abstrakt, symbolisch, bildlich oder konkret sein. Die Verwendung vieler verschiedener Darstellungen für dasselbe Wissen und die Übersetzung von Schülern zwischen Darstellungen hilft dem Schüler, Wissenstypen miteinander in Beziehung zu setzen und das Wissen mit physischer Erfahrung in Beziehung zu setzen. Es fördert die Bildung von Verbindungen zwischen Wissenselementen und fördert eine reiche Clusterbildung von Wissen.
2. Machen Sie Vorwärts- und Rückwärtsreferenzen. Konzepte erfordern eine lange Zeit, um gebildet zu werden. Daher können Sie nicht warten, bis die Schüler ein Thema vollständig gelernt haben, bevor Sie mit dem nächsten fortfahren. Indem Sie Vorwärtsreferenzen erstellen, bereiten Sie den Schüler auf neues Material vor. Indem Sie Rückwärtsreferenzen erstellen, verknüpfen Sie neues Material mit etabliertem (oder teilweise etabliertem) Material, wodurch Wissen verwoben und miteinander verbunden wird und nicht linear.
3. Erweiterte Kontexte erkunden. Konzepte können extrem kontextabhängig sein und werden erst global nützlich, wenn sie abstrahiert sind. Die Untersuchung eines breiten Kontextes der Anwendbarkeit hilft dem Schüler, Konzepte zu verfeinern und zu abstrahieren. Es vermeidet auch falsche oder stark vereinfachte Verallgemeinerungen.
4. Vergleichen und kontrastieren. Wesentlich für den Prozess der Strukturierung (oder Umstrukturierung) von Wissen ist die Klassifizierung und Wechselbeziehung von Wissenselementen. Vergleiche und Kontraste sensibilisieren die Schüler für Kategorien und Beziehungen und helfen den Schülern, die Gemeinsamkeiten und Unterschiede wahrzunehmen, die zur Organisation ihres Wissensspeichers erforderlich sind.
5. Kategorisieren und klassifizieren. Parallel zu Vergleichen und Kontrasten müssen die Schüler Kategorien und Klassifizierungssysteme kennen. Die Schüler müssen auch das Erstellen und Erkennen von Kategorisierungssystemen üben. Indem wir die Schüler auffordern, Elemente zu klassifizieren, Namen für ihre Kategorien zu wählen und ihr System zu erklären, können wir den Schülern helfen, ihren Wissensspeicher neu zu strukturieren.
6. & Anzeigen (Unzulänglichkeit des alten Modells). Sorgfältig ausgewählte Demonstrationen und Experimente können verwendet werden, um Inkonsistenzen in Schülermodellen aufzudecken. Den Schülern sollte ein Aufbau- oder Versuchsapparat gezeigt werden und sie sollten gebeten werden, vorherzusagen, was passieren wird, wenn etwas getan wird. Es ist wichtig, dass die Schüler im Voraus Vorhersagen treffen und sie so auf ihr eigenes Modell aufmerksam machen. Die Schüler werden alternative Konzepte nur in Betracht ziehen, wenn ihre eigenen fehlschlagen. Wenn die Schüler aufgefordert werden, ihre Modelle zu verwenden, und ihnen zeigen, wie inkonsistent oder unzureichend ihre Modelle sind, können sie bessere (wenn auch immer noch ihre eigenen) Modelle erstellen.

7. Erklären (zusammenfassen, beschreiben, diskutieren, definieren usw.). Standardprobleme sagen dem Lehrer selten, was die Schüler nicht verstehen. Selbst wenn die Schüler ein Problem richtig stellen, kann es immer noch zu Verwirrung über die Anwendbarkeit der verwendeten Gleichungen kommen. Wenn die Schüler erklären müssen, wie sie ein Problem lösen, werden Missverständnisse und Missverständnisse aufgedeckt, und hilft den Schülern, ihren Wissensspeicher neu zu organisieren. Darüber hinaus sehen Studenten in Standarddemonstrationen und Experimenten selten, was Experten sehen. Die Schüler sollten erklären und diskutieren, was sie ihrer Meinung nach gesehen haben (z. B. während der & -Show), damit der Lehrer mit den Modellen der Schüler interagieren kann. Darüber hinaus ist der Prozess des Erklärens (oder Zusammenfassens, Beschreibens, Diskutierens usw.) hilft den Schülern, sich ihrer eigenen Modelle sowie der Modelle anderer Schüler bewusst zu werden.

8. Generieren Sie mehrere Lösungen. Eine effiziente Problemlösung kann nur erfolgen, wenn die Schüler aus einer Reihe gültiger Lösungspfade auswählen. Indem sie Probleme auf mehr als eine Weise lösen, lernen die Schüler, Elemente ihres strategischen Wissens zu priorisieren.

9. Planen, begründen und strategisieren. Sehr wenige Beziehungen in der Physik sind immer gültig. Um Gleichungsmanipulationen zu vermeiden, sollten die Schüler gebeten werden, zu planen (und dann zu erklären), wie sie Probleme lösen werden. Die Studierenden müssen lernen, wie sie bestimmen, welche Konzepte für eine bestimmte Problemsituation relevant (und welche irrelevant) sind, und wie sie die relevanten Konzepte implementieren, um dieses Problem zu lösen. Wenn die Schüler ihre eigenen Strategien entwickeln, lernen sie, wie Konzepte zur Lösung von Problemen verwendet werden.
10. Reflektieren (auswerten, integrieren, erweitern, verallgemeinern usw. Nach Abschluss der meisten Aktivitäten profitieren die Schüler davon, auf das zurückzublicken, was sie getan haben. Welche Muster haben sie wahrgenommen? Welche allgemeinen Regeln können konstruiert werden? Andere Arten von Aktivitäten geben den Schülern die Teile, die benötigt werden, um ein kohärentes Bild der Physik zu erstellen, aber normalerweise ist eine Art reflektierende Aktivität erforderlich, um „die Teile zusammenzusetzen“.
11. Meta-Kommunikation über den Lernprozess. Um Physik (oder ein anderes komplexes Fach) zu lernen, müssen sich die Schüler selbst investieren. Sie müssen den Modellen anderer Menschen (Lehrer und Schüler) ausgesetzt sein. Sie müssen gewarnt werden, dass Präzision in der Kommunikation unerlässlich ist; sie müssen über häufige Fallstricke und Fehlinterpretationen informiert werden; und ihnen muss gesagt werden, dass sie ihr Wissen neu strukturieren sollten. Die Schüler müssen lernen, wie sie am besten lernen.