Estacionariedad significa que las propiedades estadísticas de una serie de tiempo es decir, la media, la varianza y la covarianza no cambian con el tiempo. Muchos modelos estadísticos requieren que la serie sea estacionaria para hacer predicciones efectivas y precisas.
Se usarían dos pruebas estadísticas para verificar la estacionalidad de una prueba de Dickey Fuller Aumentada en serie temporal («ADF») y una prueba de Kwiatkowski – Phillips-Schmidt-Shin («KPSS»). También se utilizará un método para convertir una serie temporal no estacionaria en series estacionarias.
Esta primera celda importa paquetes estándar y establece que las gráficas aparezcan en línea.
:
%matplotlib inlineimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport statsmodels.api as sm
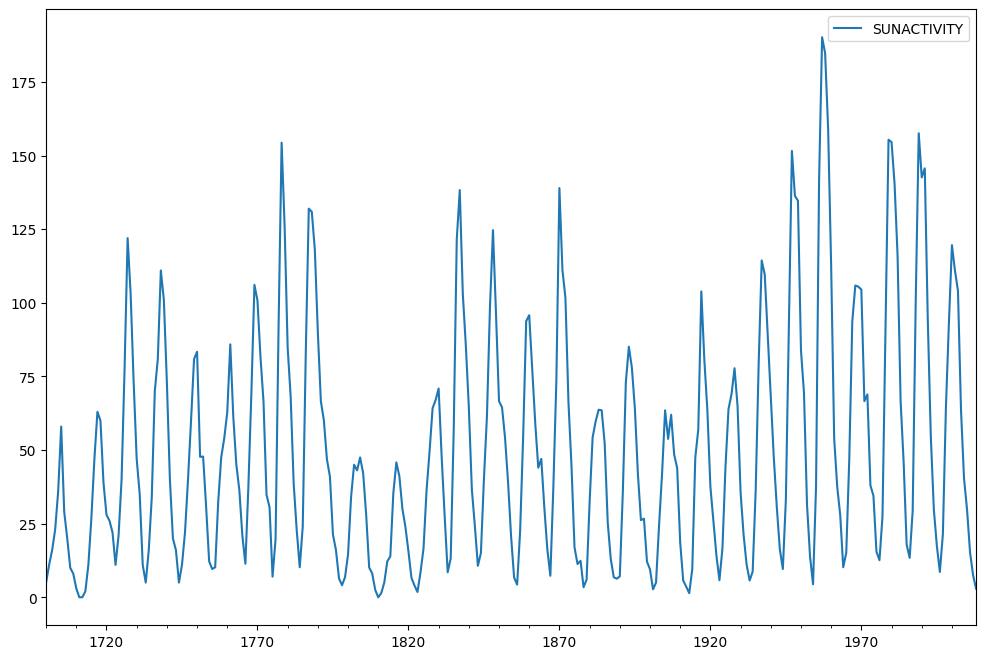
las Manchas solares conjunto de datos se utiliza. Contiene datos anuales (1700-2008) sobre manchas solares del Centro Nacional de Datos Geofísicos.
:
sunspots = sm.datasets.sunspots.load_pandas().data
Algunos de preprocesamiento se lleva a cabo en los datos. La columna » AÑO » se utiliza para crear el índice.
:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))del sunspots
se trazan Los datos ahora.
:
sunspots.plot(figsize=(12,8))
:
<AxesSubplot:>
Prueba de ADF¶
La prueba de ADF se utiliza para determinar la presencia de raíz unitaria en la serie, y por lo tanto ayuda a comprender si la serie es estacionaria o no. La hipótesis nula y alternativa de esta prueba son:
Hipótesis nula: La serie tiene una raíz unitaria.
Hipótesis alternativa: La serie no tiene raíz unitaria.
Si no se ha rechazado la hipótesis nula, esta prueba puede proporcionar pruebas de que la serie no es estacionaria.
Se crea una función para llevar a cabo la prueba ADF en una serie temporal.
:
from statsmodels.tsa.stattools import adfullerdef adf_test(timeseries): print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC') dfoutput = pd.Series(dftest, index=) for key,value in dftest.items(): dfoutput = value print (dfoutput)
prueba KPSS¶
KPSS es otra prueba para comprobar la estacionariedad de una serie de tiempo. La hipótesis nula y alternativa para la prueba KPSS son opuestas a la prueba ADF.
Hipótesis nula: El proceso es estacionario de tendencia.
Hipótesis alternativa: La serie tiene una raíz unitaria (la serie no es estacionaria).
Se crea una función para llevar a cabo la prueba KPSS en una serie temporal.
:
from statsmodels.tsa.stattools import kpssdef kpss_test(timeseries): print ('Results of KPSS Test:') kpsstest = kpss(timeseries, regression='c', nlags="auto") kpss_output = pd.Series(kpsstest, index=) for key,value in kpsstest.items(): kpss_output = value print (kpss_output)
Las pruebas de ADF dan los siguientes resultados: estadística de prueba, valor de p y el valor crítico a intervalos de confianza del 1%, 5% y 10%.
La prueba ADF ahora se aplica a los datos.
:
adf_test(sunspots)
Results of Dickey-Fuller Test:Test Statistic -2.837781p-value 0.053076#Lags Used 8.000000Number of Observations Used 300.000000Critical Value (1%) -3.452337Critical Value (5%) -2.871223Critical Value (10%) -2.571929dtype: float64
Basado en el nivel de significancia de 0.05 y el valor p de la prueba ADF, la hipótesis nula no puede ser rechazada. Por lo tanto, la serie no es estacionaria.
Las pruebas KPSS dan los siguientes resultados: estadística de prueba, valor p y el valor crítico a intervalos de confianza del 1%, 5% y 10%.
La prueba KPSS ahora se aplica a los datos.
:
kpss_test(sunspots)
Results of KPSS Test:Test Statistic 0.669866p-value 0.016285Lags Used 7.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
Basado en el nivel de significancia de 0.05 y el valor p de la prueba KPSS, no hay evidencia para rechazar la hipótesis nula en favor de la alternativa. Por lo tanto, la serie no es estacionaria según la prueba KPSS.
Siempre es mejor aplicar ambas pruebas, de modo que se pueda garantizar que la serie sea realmente estacionaria. Los posibles resultados de la aplicación de estas pruebas estacionarias son los siguientes:
Aquí, debido a la diferencia en los resultados de la prueba ADF y la prueba KPSS, se puede inferir que la serie es estacionaria de tendencia y no estacionaria estricta. La serie se puede desviar por diferenciación o por ajuste de modelo.
Restar importancia por diferenciación¶
Es uno de los métodos más simples para restar importancia a una serie temporal. Se construye una nueva serie en la que el valor en el paso de tiempo actual se calcula como la diferencia entre la observación original y la observación en el paso de tiempo anterior.
Se aplica la diferenciación a los datos y se representa el resultado.
:
sunspots = sunspots - sunspots.shift(1)sunspots.dropna().plot(figsize=(12,8))
:
<AxesSubplot:>
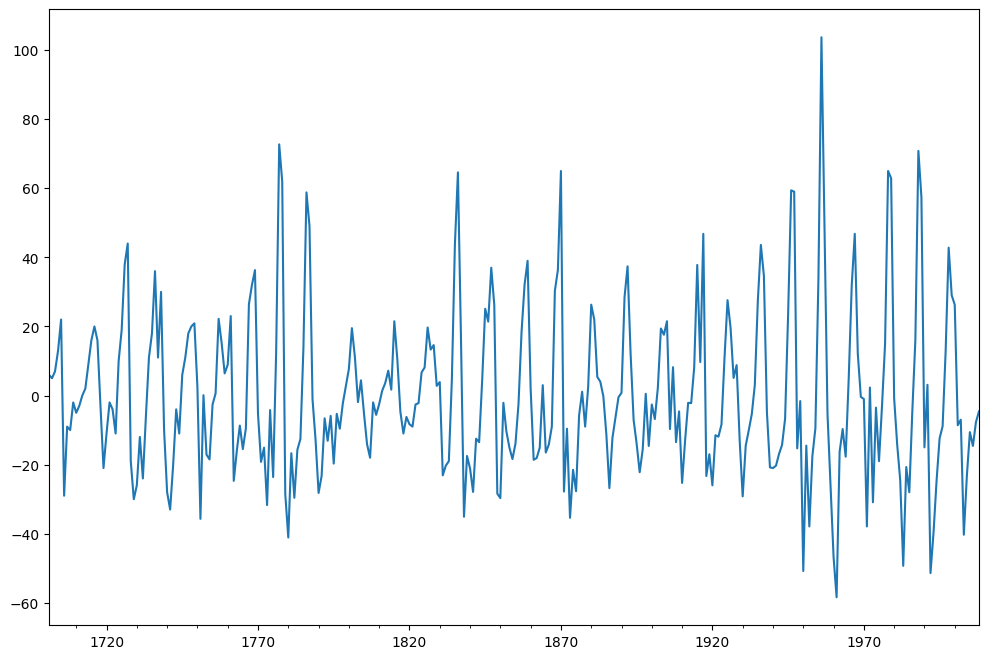
Ahora se aplica la prueba ADF a estos valores desviados y se comprueba la estacionalidad.
:
adf_test(sunspots.dropna())
Results of Dickey-Fuller Test:Test Statistic -1.486166e+01p-value 1.715552e-27#Lags Used 7.000000e+00Number of Observations Used 3.000000e+02Critical Value (1%) -3.452337e+00Critical Value (5%) -2.871223e+00Critical Value (10%) -2.571929e+00dtype: float64
Basado en el valor p de la prueba ADF, no hay evidencia para rechazar la hipótesis nula en favor de la alternativa. Por lo tanto, la serie es estrictamente estacionaria ahora.
Ahora se aplica la prueba KPSS a estos valores desviados y se comprueba la estacionalidad.
:
kpss_test(sunspots.dropna())
Results of KPSS Test:Test Statistic 0.021193p-value 0.100000Lags Used 0.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/stattools.py:1911: InterpolationWarning: The test statistic is outside of the range of p-values available in thelook-up table. The actual p-value is greater than the p-value returned. warn_msg.format(direction="greater"), InterpolationWarning
Basado en el valor p de la prueba KPSS, la hipótesis nula no puede ser rechazada. Por lo tanto, la serie es estacionaria.
Conclusión¶
Se utilizan dos pruebas para verificar la estacionalidad de una serie temporal, a saber, prueba ADF y prueba KPSS. El desaprovechamiento se lleva a cabo mediante el uso de la diferenciación. Las series temporales estacionarias de tendencia se convierten en series temporales estacionarias estrictas. El modelo de pronóstico requerido ahora se puede aplicar a datos de series temporales estacionarias.