Estructura del Conocimiento

Extraído de un folleto que acompaña a un taller para profesores de ciencias de secundaria.

por Robert J. Dufresne, William J. Leonard y William J. Gerace

Nuestro grupo en UMass ha desarrollado un modelo cognitivo que nos ayuda a representar las diferencias en las formas en que los expertos y los novatos almacenan y utilizan el conocimiento del contenido. El Modelo también nos ayuda a enfocarnos en áreas específicas en las que los novatos necesitan concentrarse para convertirse en mejores solucionadores de problemas. Sin embargo, el Modelo es solo una representación de la estructura del conocimiento, y está en constante evolución. Por lo tanto, no debe tomarse demasiado literalmente. Su utilidad proviene de su capacidad de proporcionar una manifestación concreta, aunque imperfecta, de las formas en que piensan expertos y novatos. El Modelo nos ayuda a discutir:

1. el almacenamiento de conocimiento específico del dominio;
2. comportamiento de resolución de problemas de tipo experto y novato;
3. la estructura jerárquica del almacén de conocimientos de un experto;
4. conceptos erróneos;
5. los efectos de las preguntas sin metas y dirigidas a metas; y
6. el proceso de metacomunicación.

En este taller—y en nuestro enfoque de la física en general – – – hay 3 temas básicos:

1. Se necesitan tipos particulares de conocimientos y estructuras de conocimiento para resolver problemas de manera competente. Gran parte de este conocimiento es de naturaleza conceptual, a diferencia de operacional o de procedimiento, y las poderosas estructuras de conocimiento necesariamente involucran elementos conceptuales. La presencia de elementos conceptuales en las estructuras de conocimiento es la clave para tener una «comprensión más profunda» de la física.
2. Se requieren tipos particulares de procesos cognitivos para la adquisición de conocimientos conceptuales y la construcción de estructuras de conocimiento útiles.
3. Es posible diseñar actividades que promuevan estos procesos cognitivos deseables. En muchos casos, estas actividades son simplemente actualizaciones de los procesos cognitivos en sí mismos. (Este punto, con suerte, se aclarará más adelante.)

Desarrollaremos cada uno de estos temas antes de centrarnos en ejemplos específicos.

Tema 1: ¿Qué necesitan saber los estudiantes y cómo se debe estructurar lo que saben para resolver problemas de manera eficiente?

Comenzamos identificando algunos de los diversos tipos de conocimiento que los estudiantes necesitan conocer:

• Conocimiento conceptual, como el concepto de momento o energía, o que la velocidad de un objeto cambia cuando se acelera, o que la energía potencial gravitacional de un objeto disminuye a medida que cae.
• Conocimiento fáctico, como el valor de la constante gravitacional g, el radio de la luna o la densidad del hierro.
• Conocimiento de representación, como dibujar y usar gráficos.
• Conocimiento estratégico, como la capacidad de reconocer la aplicabilidad de un concepto, como, el momento se conserva cuando no hay fuerzas externas, o que la energía se conserva cuando no hay fuerzas no conservadoras.
• Conocimiento meta-cognitivo, por ejemplo, la conciencia de suposiciones subyacentes, o que una respuesta debe verificarse resolviendo el problema de una manera diferente.
• Autoconocimiento, como conocer las fuentes probables de errores, o saber que uno debe ser más procedimental al resolver problemas.
• Conocimiento operativo, como cómo tomar el producto cruzado o el producto escalar de dos vectores, o cómo tomar el determinante de una matriz, o cómo dibujar un diagrama de cuerpo libre.
• Conocimiento de procedimientos, como cuándo usar la conservación de energía (p. ej., cuando todas las fuerzas son conservadoras), o cuándo especificar un sistema de coordenadas (por ejemplo, al encontrar energía potencial), o cuándo dibujar un diagrama de cuerpo libre (por ejemplo, al aplicar las Leyes de Newton).
• Conocimiento del estado del problema, que son las características de un problema que se utilizan para decidir cómo resolverlo. Algunos ejemplos son: saber que no existen fuerzas externas en un problema en particular, o que no hay fuerzas conservadoras en el problema, o que un objeto está en reposo inicialmente, o que el objeto está en una pendiente.

Estos tipos de conocimiento deben organizarse y estructurarse para un uso eficiente a la hora de resolver problemas. Para discutir los aspectos organizativos y estructurales del conocimiento, hemos encontrado conveniente clasificar ampliamente estos tipos en tres categorías generales. Llamamos a estos tres grupos: Conocimiento Conceptual, Conocimiento Operacional y de Procedimiento, y Conocimiento del Estado Problema. En la Fig. 1, estas tres categorías generales se muestran en una representación de cómo los expertos almacenan el conocimiento del contenido.

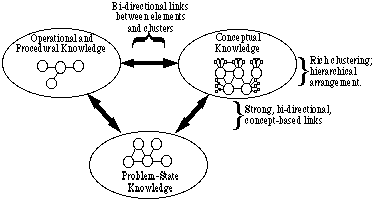Fig. 1: Una representación de la estructura de conocimiento de un experto

El experto tiene una rica agrupación de conceptos, en la que cada concepto está relacionado con muchos otros conceptos, y las relaciones entre conceptos se entienden claramente. Los conceptos se ordenan jerárquicamente utilizando conceptos paraguas para relacionarlos más estrechamente. De hecho, los conceptos paraguas se utilizan para agrupar elementos dentro de cada una de las tres categorías. El experto tiene un gran acervo de conocimientos sobre el estado del problema, incluida mucha información sobre los principios que se aplican a situaciones particulares. El experto también tiene una gran cantidad de ecuaciones, operaciones y procedimientos (EOPs) a los que se puede acceder rápidamente.

Los vínculos entre cada par de categorías son muy fuertes: los estados problemáticos están fuertemente vinculados a conceptos y a EOPs, que a su vez están fuertemente vinculados entre sí. Los mismos conceptos generales se utilizan para agrupar conceptos, estados problemáticos y EOPs. Por lo tanto, para cualquier problema en particular, los conceptos se pueden usar para decidir la idoneidad y aplicabilidad de las ecuaciones, y la utilidad de operaciones y procedimientos específicos.

(Uno debe tener mucho cuidado de no ser demasiado rígido en el pensamiento, porque es fácil estar en desacuerdo sobre cuál de estas categorías debe usarse para clasificar un elemento de conocimiento en particular, o si pertenece solo a una categoría. Nuestro propósito es simplemente tener un mecanismo para visualizar los varios niveles de asociación que pueden ocurrir entre los elementos.)

Tendemos a usar el término vinculación para significar una asociación formada entre dos elementos del mismo o diferentes tipos de conocimiento, y el término agrupación para referirse a asociaciones entre varios elementos o grupos. Lo que hace que este tipo de discusión sea muy difícil es que hay una especie de proceso iterativo en curso aquí: Un vínculo muy fuerte entre tres elementos-un clúster conceptual, el reconocimiento de las circunstancias que hacen que el concepto sea aplicable y los procedimientos necesarios para aplicarlo-forma un nuevo tipo de elemento de conocimiento que ponemos en Conocimiento Estratégico (una cuarta categoría). Este nuevo elemento de conocimiento es lo que algunos se refieren como un esquema y a menudo involucra también el conocimiento del estado problema. Dado que el elemento de conocimiento es de naturaleza conceptual, se replica (es decir, se repite) en la burbuja conceptual.

Si echamos un vistazo más de cerca a la burbuja conceptual, vemos algunos de los tipos específicos de conocimiento conceptual, por ejemplo, Conocimiento Representacional, Conocimiento Estratégico, Conocimiento Meta-Cognitivo y Conocimiento de Conceptos Básicos. Esto se representa en la Fig. 2. (No se muestran otros tipos de conocimiento conceptual.)

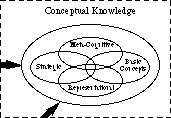Fig. 2: Tipos de conocimiento conceptual

¿En qué se diferencia la estructura de conocimiento de un novato de la de un experto? Como se representa en la Fig. 3, los principiantes generalmente tienen un pobre agrupamiento de conceptos. Muchos enlaces son inapropiados; otros no existen. Algunos de los enlaces inapropiados son extremadamente fuertes, lo que conduce a conceptos erróneos. Los principiantes generalmente no usan conceptos de paraguas para agrupar elementos. Tienen un pequeño almacén de situaciones problemáticas, en las que las características de la superficie se utilizan para agruparlas y decidir cómo se deben resolver los problemas. Están familiarizados con un número relativamente grande de ecuaciones, pero a menudo las recuerdan incorrectamente o necesitan buscarlas para usarlas. Se les han enseñado operaciones y procedimientos, pero todavía no son competentes en ellos. Por lo tanto, no se puede decir que los «conocen».

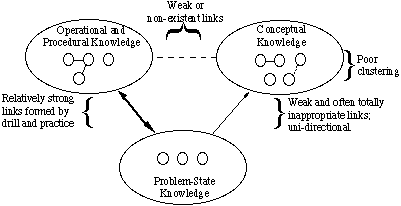Fig. 3: Una representación de la estructura de conocimiento del novato

Los vínculos entre conceptos y EOPs son débiles o inexistentes. Los vínculos entre conceptos y situaciones problemáticas también son débiles. Por lo tanto, un novato no puede analizar un problema y no puede decidir la idoneidad de ecuaciones particulares. Los vínculos entre situaciones problemáticas y EOPs son relativamente fuertes, pero los vínculos se basan principalmente en las cantidades que las ecuaciones tienen en común con los datos y las incógnitas explícitas del problema.

Tema 2: ¿En qué tipos de procesos cognitivos deben participar los estudiantes para desarrollar estructuras de conocimiento apropiadas?

Para responder a esta pregunta, primero debemos comprender cómo los expertos y los principiantes resuelven los problemas de manera diferente.

Los principiantes generalmente no tienen éxito cuando intentan resolver problemas típicos en física. Usando el Modelo para representar el proceso, ¿cómo resuelve un problema un principiante típico? Debido a que los vínculos más fuertes en la estructura de conocimiento del principiante se encuentran entre situaciones problemáticas y ecuaciones, la lectura de un problema sugiere inmediatamente ecuaciones que involucran las cantidades (conocidas y desconocidas) explícitamente dadas en el problema. Sin determinar la aplicabilidad de esas ecuaciones, y sin tratar de pensar en otras ecuaciones que podrían involucrar las mismas cantidades, el novato generalmente comienza a manipular las ecuaciones más familiares hasta que se pueda resolver lo desconocido. La ecuación más reciente cubierta en la clase es la más fácilmente accesible y la más rápidamente recuperada. Por lo tanto, el novato busca y (si tiene «éxito») encuentra solo una forma de resolver un problema y generalmente se detiene, sin investigar otras posibilidades y sin analizar la situación del problema. Las ecuaciones encontradas de esta manera a menudo son inapropiadas porque los principiantes a menudo no usan conceptos para justificar su aplicación. Incluso si los estudiantes se ven impulsados a invocar conceptos mediante el análisis de problemas de antemano, sus vínculos con EOPs generalmente son demasiado débiles para ser útiles para resolver problemas. Además, los vínculos entre conceptos y situaciones problemáticas son unidireccionales, por lo que las analogías no son particularmente útiles: Los principiantes no pueden usar analogías para resolver problemas porque no pueden identificar cuáles de los problemas que ya han resuelto son conceptualmente similares al que están tratando de resolver actualmente. En su lugar, los principiantes usan características de superficie para establecer «similitud» e intentar resolver nuevos problemas en función de su similitud con las características de superficie de problemas que ya han resuelto.

Debido a que los expertos clasifican los problemas y las EOPs de acuerdo con los mismos conceptos generales, a menudo pueden pasar directamente de situaciones problemáticas a ecuaciones, operaciones y/o procedimientos apropiados. Debido a que los vínculos entre las diferentes categorías son problemas fuertes y difíciles (aquellos para los que aún no existe un vínculo directo entre los estados problemáticos y las OEEE), se pueden resolver invocando conceptos conscientemente, conectando así indirectamente los estados problemáticos con las OEEE apropiadas. Debido a que los vínculos entre conceptos y situaciones problemáticas son bidireccionales, las analogías son una herramienta de resolución de problemas extremadamente útil para los expertos. Por último, los expertos suelen tener más de un enfoque para resolver cualquier problema en particular.

Aquí hay un resumen de las principales diferencias entre expertos y novatos:

1. Los principiantes tienen una mala agrupación de conceptos, lo que a menudo conduce a conceptos erróneos. Los expertos tienen una rica agrupación de conceptos, situaciones problemáticas, ecuaciones, procedimientos y operaciones, lo que conduce a una mejor capacidad de resolución de problemas.
2. Los novatos generalmente tienen una sola forma de resolver un problema en particular, mientras que los expertos a menudo pueden encontrar más de una manera. Por lo tanto, el experto puede intentar resolver las inconsistencias cuando ocurren y verificar las respuestas, mientras que los novatos no saben que existen inconsistencias y no pueden verificar sus respuestas.
3. Los principiantes a menudo usan la manipulación de ecuaciones y rara vez usan estrategias basadas en conceptos para obtener una respuesta. El experto utiliza conceptos y analogías para sugerir varios métodos de solución y planea una estrategia para encontrar la respuesta correcta.
4. Los novatos a menudo no obtienen la respuesta correcta, y cuando obtienen la respuesta correcta, puede ser fácilmente por la razón equivocada. Cuando el novato obtiene la respuesta correcta por la razón equivocada, los conceptos erróneos se refuerzan y se vuelven aún más difíciles de superar. Por lo general, un experto obtiene la respuesta correcta y puede explicar por qué la respuesta es correcta.

Hay una variedad de procesos cognitivos beneficiosos para ayudar a los principiantes a desarrollar un enfoque de resolución de problemas basado en conceptos, que dividimos en tres categorías: Procesos de Análisis, Procesos de Razonamiento y Procesos Meta-Cognitivos.

Análisis de procesos

• Análisis de problemas, como la construcción de una representación de problemas.
• Análisis conceptual, como el uso de conceptos para determinar el comportamiento cualitativo de objetos físicos o para formar una estrategia.
• Análisis estratégico, como identificar y justificar principios físicos relevantes para una situación problemática.
• Análisis representacional, como explorar diferentes representaciones de un problema.
• Análisis constructivo complejo, como descomponer una situación compleja en otras más simples.

Procesos de razonamiento

• Comparar y contrastar, como identificar cómo los elementos, las situaciones o las condiciones son similares y/o diferentes.
• Interpretar, por ejemplo, utilizando la forma de una parcela de posición vs tiempo para estimar la aceleración del objeto.
• Casos especiales y limitantes, es decir, explorar condiciones extremas y / o conocidas.
• Prototipos y contraejemplos, por ejemplo, generando categorías arquetípicas.
• Generalización, es decir, reconocer las características sobresalientes de una circunstancia o situación.

Procesos meta-cognitivos

• Reflexión, es decir, revisión autodirigida del propósito, las metas, los efectos de la experiencia, etc.
• Meta-comunicación, que es la participación consciente en establecer y refinar líneas de comunicación con el maestro y otros estudiantes, y en decidir los objetivos del aprendizaje.
• Autoevaluación, como evaluar el desempeño o identificar las razones por las que se encontraron dificultades al resolver un problema.

Estos y otros procesos son alentados por nuestros materiales curriculares. Los tipos específicos de actividades para hacer esto se presentan en la siguiente sección.

Tema 3: ¿Qué tipos de actividades o experiencias de aprendizaje promueven estos procesos cognitivos beneficiosos?

Los profesores pueden utilizar las siguientes actividades para estimular los procesos cognitivos necesarios para desarrollar una comprensión conceptual de la física:

1. Utilice varias representaciones. Una representación puede ser lingüística, abstracta, simbólica, pictórica u concreta. Usar muchas representaciones diferentes para el mismo conocimiento, y hacer que los estudiantes traduzcan entre representaciones, ayuda al estudiante a relacionar los tipos de conocimiento y relacionar el conocimiento con la experiencia física. Fomenta la formación de vínculos entre los elementos del conocimiento y promueve una rica agrupación de conocimientos.
2. Haga referencias hacia adelante y hacia atrás. Los conceptos requieren mucho tiempo para formarse. Por lo tanto, no puede esperar a que los estudiantes aprendan completamente un tema antes de pasar al siguiente. Al hacer referencias, usted prepara al estudiante para material nuevo. Al hacer referencias hacia atrás, asocias material nuevo con material establecido (o parcialmente establecido), haciendo que el conocimiento se entrelace e interconecte, en lugar de ser lineal.
3. Explorar contextos extendidos. Los conceptos pueden ser extremadamente dependientes del contexto y no se vuelven útiles globalmente hasta que se abstraen. Investigar un contexto amplio de aplicabilidad ayuda al estudiante a refinar y abstraer conceptos. También evita generalizaciones incorrectas o simplificadas en exceso.
4. Comparar y contrastar. La clasificación y la interrelación de los elementos del conocimiento son esenciales para el proceso de estructuración (o reestructuración) del conocimiento. Las comparaciones y contrastes sensibilizan a los estudiantes sobre categorías y relaciones, y les ayudan a percibir los puntos en común y las distinciones necesarias para organizar su almacén de conocimientos.
5. Categorizar y clasificar. Paralelamente a las comparaciones y contrastes, los estudiantes deben conocer las categorías y los sistemas de clasificación. Los estudiantes también deben practicar la creación y el reconocimiento de sistemas de categorización. Al exigir a los estudiantes que clasifiquen los elementos, elijan los nombres de sus categorías y expliquen su sistema, podemos ayudar a los estudiantes a reorganizar su almacén de conocimientos.
6. Predecir & Mostrar (inadecuación del modelo antiguo). Se pueden utilizar demostraciones y experimentos cuidadosamente seleccionados para mostrar inconsistencias en los modelos de los estudiantes. A los estudiantes se les debe mostrar una configuración o un aparato experimental y se les debe pedir que predigan lo que sucederá cuando se haga algo. Es importante que los estudiantes hagan predicciones de antemano, haciéndoles conscientes de su propio modelo. Los estudiantes considerarán concepciones alternativas solo si sus propias fallas. Exigir a los estudiantes que usen sus modelos y mostrarles cómo sus modelos son inconsistentes o inadecuados los preparará para crear mejores modelos (aunque todavía sean propios).

7. Explicar (resumir, describir, discutir, definir, etc.). Los problemas estándar rara vez le dicen al maestro lo que los estudiantes no entienden. Incluso cuando los estudiantes aciertan con un problema, todavía puede haber confusión sobre la aplicabilidad de las ecuaciones utilizadas. Exigir a los estudiantes que expliquen cómo resolverán un problema expone malentendidos y conceptos erróneos, y ayuda a los estudiantes a reorganizar su almacén de conocimientos. Además, los estudiantes rara vez ven en demostraciones y experimentos estándar lo que ven los expertos. Los estudiantes deben explicar y discutir lo que creen que han visto (durante el programa Predict &, por ejemplo), para que el maestro pueda interactuar con los modelos de los estudiantes. Además, el proceso de explicar (o resumir, describir, discutir, etc.) ayuda a los estudiantes a tomar conciencia de sus propios modelos, así como de los modelos de otros estudiantes.

8. Genere múltiples soluciones. La resolución de problemas eficiente no puede ocurrir a menos que los estudiantes elijan entre un conjunto de rutas de solución válidas. Al resolver problemas de más de una manera, los estudiantes aprenden a priorizar elementos de su Conocimiento Estratégico.

9. Planifique, justifique y elabore estrategias. Muy pocas relaciones en física son siempre válidas. Para evitar la manipulación de ecuaciones, se debe pedir a los estudiantes que planifiquen (y luego expliquen) cómo resolverán los problemas. Los estudiantes deben aprender a determinar qué conceptos son relevantes (y cuáles son irrelevantes) para cualquier situación de problema en particular y cómo implementar los conceptos relevantes para resolver ese problema. Hacer que los estudiantes generen sus propias estrategias les ayuda a aprender cómo se utilizan los conceptos para resolver problemas.
10. Reflejar (evaluar, integrar, extender, generalizar, etc. Después de completar la mayoría de las actividades, los estudiantes se benefician de mirar hacia atrás en lo que han hecho. ¿Qué patrones han percibido? ¿Qué reglas generales se pueden construir? Otros tipos de actividades dan a los estudiantes las piezas necesarias para crear una imagen coherente de la física, pero generalmente se necesita algún tipo de actividad reflexiva para «unir las piezas».
11. Meta-comunicar sobre el proceso de aprendizaje. Para aprender física (o cualquier otra asignatura compleja), los estudiantes deben invertir en sí mismos. Deben estar expuestos a los modelos de otras personas (maestros y estudiantes). Se les debe advertir que la precisión en la comunicación es esencial; se les debe informar de las dificultades comunes y las interpretaciones erróneas; y se les debe decir que deben reestructurar su conocimiento. Los estudiantes deben aprender cómo aprenden mejor.