Lo básico: KNN para clasificación y regresión

Ciencia de datos desde cero

Los cursos de ciencia de datos o estadística aplicada generalmente comienzan con modelos lineales, pero a su manera, K-nearest neighbors es probablemente el modelo más simple ampliamente utilizado conceptualmente. Los modelos KNN son en realidad solo implementaciones técnicas de una intuición común, que las cosas que comparten características similares tienden a ser, bueno, similares. Esto no es una visión profunda, sin embargo, estas implementaciones prácticas pueden ser extremadamente poderosas y, fundamentalmente para alguien que se acerca a un conjunto de datos desconocido, pueden manejar no linealidades sin ninguna ingeniería de datos complicada o configuración de modelos.

What

Como ejemplo ilustrativo, consideremos el caso más simple de usar un modelo KNN como clasificador. Digamos que tienes puntos de datos que caen en una de tres clases. Un ejemplo bidimensional puede tener este aspecto:

Probablemente pueda ver con bastante claridad que las diferentes clases están agrupadas: la esquina superior izquierda de los gráficos parece pertenecer a la clase naranja, la sección derecha/central a la clase azul. Si se le dieran las coordenadas de un nuevo punto en algún lugar del gráfico y se le preguntara a qué clase probablemente pertenecería, la mayoría de las veces la respuesta sería bastante clara. Cualquier punto en la esquina superior izquierda del gráfico es probable que sea naranja, etc.

La tarea se vuelve un poco menos segura entre las clases, sin embargo, donde necesitamos establecer un límite de decisión. Considere el nuevo punto agregado en rojo a continuación:

¿Este nuevo punto debe clasificarse como naranja o azul? El punto parece estar entre los dos grupos. Su primera intuición podría ser elegir el clúster que está más cerca del nuevo punto. Este sería el enfoque de «vecino más cercano», y a pesar de ser conceptualmente simple, con frecuencia produce predicciones bastante sensatas. ¿A qué punto identificado anteriormente es el nuevo más cercano? Puede que no sea obvio simplemente observar la gráfica cuál es la respuesta, pero es fácil para la computadora recorrer los puntos y darnos una respuesta:

, parece que el punto más cercano está en la categoría azul, por lo que nuestro nuevo punto probablemente también lo esté. Ese es el método del vecino más cercano.

En este punto, es posible que se pregunte para qué sirve la ‘k’ en k-vecinos más cercanos. K es el número de puntos cercanos que el modelo observará al evaluar un nuevo punto. En nuestro ejemplo de vecino más cercano más simple, este valor para k era simplemente 1: miramos al vecino más cercano y eso fue todo. Sin embargo, podría haber elegido mirar los 2 o 3 puntos más cercanos. ¿Por qué es esto importante y por qué alguien pondría k en un número más alto? Por un lado, los límites entre clases podrían toparse uno al lado del otro de manera que sea menos obvio que el punto más cercano nos dará la clasificación correcta. Considere las regiones azul y verde en nuestro ejemplo. De hecho, vamos a acercarlos:

Observe que, si bien las regiones en general parecen lo suficientemente distintas, sus límites parecen estar un poco entrelazados entre sí. Esta es una característica común de los conjuntos de datos con un poco de ruido. Cuando este es el caso, se hace más difícil clasificar las cosas en las áreas fronterizas. Considere este nuevo punto:

Por un lado, visualmente definitivamente parece que el punto más cercano identificado previamente es azul, lo que nuestro ordenador puede confirmar fácilmente para nosotros:

Por otro lado, ese punto azul más cercano parece un poco atípico en sí, lejos del centro de la región azul y rodeado de puntos verdes. ¡Y este nuevo punto está incluso en el exterior de ese punto azul! ¿Y si miramos los tres puntos más cercanos al nuevo punto rojo?

O, incluso, el más cercano a cinco puntos hasta el nuevo punto?

Ahora parece que nuestro nuevo punto está en una zona verde! Resulta que tenía un punto azul cercano, pero la preponderancia o puntos cercanos son verdes. En este caso, tal vez tendría sentido establecer un valor más alto para k, mirar un puñado de puntos cercanos y hacer que voten de alguna manera sobre la predicción del nuevo punto.

El problema que se ilustra es excesivo. Cuando k se establece en uno, el límite entre las regiones identificadas por el algoritmo como azul y verde es irregular, serpentea hacia adelante con cada punto individual. El punto rojo parece que podría estar en la región azul:

, elevando k a 5, sin embargo, suaviza el límite de decisión a medida que los diferentes puntos cercanos votan. El punto rojo ahora parece firmemente en el vecindario verde:

La compensación con valores más altos de k es la pérdida de granularidad en el límite de decisión. Establecer k muy alto tenderá a darle límites suaves, pero los límites del mundo real que está tratando de modelar pueden no ser perfectamente suaves.

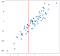
En términos prácticos, podemos usar el mismo tipo de enfoque de vecinos más cercanos para regresiones, donde queremos un valor individual en lugar de una clasificación. Considere la siguiente regresión a continuación:

Los datos se generaron aleatoriamente, pero se generaron para ser lineales, por lo que un modelo de regresión lineal se ajustaría naturalmente a estos datos. Quiero señalar, sin embargo, que puede aproximar los resultados del método lineal de una manera conceptualmente más simple con un enfoque de K-vecinos más cercanos. Nuestra ‘regresión’ en este caso no será una fórmula única como nos daría un modelo OLS, sino más bien un valor de salida mejor predicho para cualquier entrada dada. Considere el valor de -.75 en el eje x, que he marcado con una línea vertical:

Sin resolver ninguna ecuación, podemos llegar a una aproximación razonable de lo que debería ser la salida simplemente considerando los puntos cercanos:

Tiene sentido que el valor predicho esté cerca de estos puntos, no mucho más bajo o más alto. Tal vez una buena predicción sería el promedio de estos puntos:

Usted puede imaginar hacer esto para todos los posibles valores de entrada y el que viene con las predicciones en todas partes:

la Conexión de todas estas predicciones con una línea que nos da nuestra regresión:

En este caso, los resultados no son una línea limpia, pero no traza la pendiente hacia arriba de los datos razonablemente bien. Esto puede no parecer terriblemente impresionante, pero un beneficio de la simplicidad de esta implementación es que maneja bien la no linealidad. Considere esta nueva colección de puntos:

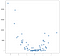
Estos puntos se generaron simplemente cuadrando los valores del ejemplo anterior, pero supongamos que se encuentra con un conjunto de datos como este en la naturaleza. Obviamente, no es de naturaleza lineal y, si bien un modelo de estilo OLS puede manejar fácilmente este tipo de datos, requiere el uso de términos no lineales o de interacción, lo que significa que el científico de datos tiene que tomar algunas decisiones sobre qué tipo de ingeniería de datos realizar. El enfoque KNN no requiere más decisiones: el mismo código que utilicé en el ejemplo lineal se puede reutilizar completamente en los nuevos datos para obtener un conjunto viable de predicciones:

Al igual que con los ejemplos de clasificadores, establecer un valor k más alto nos ayuda a evitar el sobreajuste, aunque puede comenzar a perder potencia predictiva en el margen, particularmente alrededor de los bordes de su conjunto de datos. Considere el primer conjunto de datos de ejemplo con predicciones hechas con k establecido en uno, que es un enfoque de vecino más cercano:

Nuestras predicciones saltan erráticamente a medida que el modelo salta de un punto del conjunto de datos al siguiente. Por el contrario, si se establece k en diez, de modo que se promedian juntos diez puntos totales para la predicción, se obtiene una conducción mucho más suave:

En general, eso se ve mejor, pero se puede ver algo de un problema en los bordes de los datos. Debido a que nuestro modelo tiene en cuenta tantos puntos para cualquier predicción dada, cuando nos acercamos a uno de los bordes de nuestra muestra, nuestras predicciones comienzan a empeorar. Podemos abordar este problema de alguna manera ponderando nuestras predicciones a los puntos más cercanos, aunque esto viene con sus propias compensaciones.

Cómo

Al configurar un modelo KNN, solo hay un puñado de parámetros que deben elegirse/se pueden ajustar para mejorar el rendimiento.

K: el número de vecinos: Como se discutió, el aumento de K tenderá a suavizar los límites de decisión, evitando el sobreajuste a costa de alguna resolución. No hay un valor único de k que funcione para cada conjunto de datos. Para los modelos de clasificación, especialmente si solo hay dos clases, generalmente se elige un número impar para k. Esto es para que el algoritmo nunca se encuentre con un ‘empate’: por ejemplo, mira los cuatro puntos más cercanos y encuentra que dos de ellos están en la categoría azul y dos en la categoría roja.

Métrica de distancia: Resulta que hay diferentes formas de medir qué tan «cerca» están dos puntos el uno del otro, y las diferencias entre estos métodos pueden llegar a ser significativas en dimensiones superiores. El más comúnmente utilizado es la distancia euclidiana, el tipo estándar que puede haber aprendido en la escuela secundaria usando el teorema de pitágoras. Otra métrica es la llamada «distancia de Manhattan», que mide la distancia tomada en cada dirección cardinal, en lugar de a lo largo de la diagonal (como si estuviera caminando de una intersección de calles en Manhattan a otra y tuviera que seguir la cuadrícula de calles en lugar de poder tomar la ruta más corta en línea recta). De manera más general, estas son en realidad ambas formas de lo que se llama «distancia de Minkowski», cuya fórmula es:

Cuando p se establece en 1, esta fórmula es la misma que la distancia de Manhattan, y cuando se establece en dos, la distancia euclidiana.Pesos

: Una forma de resolver el problema de un posible ‘empate’ cuando el algoritmo vota en una clase y el problema en el que nuestras predicciones de regresión empeoraron hacia los bordes del conjunto de datos es introduciendo la ponderación. Con los pesos, los puntos cercanos contarán más que los puntos más alejados. El algoritmo todavía mirará a todos los vecinos k más cercanos, pero los vecinos más cercanos tendrán más votos que los más lejanos. Esta no es una solución perfecta y plantea la posibilidad de sobreajustar de nuevo. Considere nuestro ejemplo de regresión, esta vez con pesos:

Nuestras predicciones van directamente al borde del conjunto de datos ahora, pero puede ver que nuestras predicciones ahora oscilan mucho más cerca de los puntos individuales. El método ponderado funciona razonablemente bien cuando estás entre puntos, pero a medida que te acercas más y más a cualquier punto en particular, el valor de ese punto tiene más y más influencia en la predicción del algoritmo. Si te acercas lo suficiente a un punto, es casi como poner k a uno, ya que ese punto tiene mucha influencia.

Escalado/normalización: Un último punto, pero de crucial importancia, es que los modelos KNN se pueden eliminar si diferentes variables de características tienen escalas muy diferentes. Considere un modelo que intente predecir, por ejemplo, el precio de venta de una casa en el mercado en función de características como el número de dormitorios y el total de pies cuadrados de la casa, etc. Hay más variación en el número de pies cuadrados de una casa que hay en el número de dormitorios. Por lo general, las casas solo tienen un pequeño puñado de dormitorios, y ni siquiera la mansión más grande tendrá decenas o cientos de dormitorios. Los pies cuadrados, por otro lado, son relativamente pequeños, por lo que las casas pueden variar desde cerca de, digamos, 1,000 hazañas cuadradas en el lado pequeño hasta decenas de miles de pies cuadrados en el lado grande.

Considere la comparación entre una casa de 2,000 pies cuadrados con 2 dormitorios y una casa de 2,010 pies cuadrados con dos dormitorios: 10 pies cuadrados. los pies apenas marcan la diferencia. Por el contrario, una casa de 2,000 pies cuadrados con tres dormitorios es muy diferente, y representa un diseño muy diferente y posiblemente más estrecho. Sin embargo, una computadora ingenua no tendría el contexto para entender eso. Diría que el dormitorio 3 está a solo » una «unidad de distancia del dormitorio 2, mientras que el pie cuadrado 2,010 está a «diez» del pie cuadrado 2,000. Para evitar esto, los datos de entidades deben escalarse antes de implementar un modelo KNN.

Fortalezas y debilidades

Los modelos KNN son fáciles de implementar y manejar bien las no linealidades. El ajuste del modelo también tiende a ser rápido: el ordenador no tiene que calcular ningún parámetro o valor en particular, después de todo. La compensación aquí es que, si bien el modelo se configura rápidamente, es más lento de predecir, ya que para predecir un resultado para un nuevo valor, tendrá que buscar en todos los puntos de su conjunto de entrenamiento para encontrar los más cercanos. Por lo tanto, para conjuntos de datos grandes, KNN puede ser un método relativamente lento en comparación con otras regresiones que pueden tomar más tiempo para ajustarse, pero luego hacer sus predicciones con cálculos relativamente sencillos.

Otro problema con un modelo KNN es que carece de interpretabilidad. Una regresión lineal OLS tendrá coeficientes claramente interpretables que pueden dar alguna indicación del «tamaño del efecto» de una característica dada (aunque se debe tener cierta precaución al asignar causalidad). Sin embargo, preguntar qué características tienen el mayor efecto no tiene sentido para un modelo KNN. En parte debido a esto, los modelos KNN tampoco se pueden usar realmente para la selección de características, de la manera en que una regresión lineal con un término de función de costo agregado, como ridge o lazo, puede ser, o de la manera en que un árbol de decisiones elige implícitamente qué características parecen más valiosas.