energía Cinética es la energía del movimiento. Una expresión para energía cinética se deriva mirando el caso de un objeto que se eleva a una altura relativa (por lo tanto, se trabaja en este objeto) y luego se le permite caer.
Términos Clave
o energía Cinética
Objetivos
o Derivar una expresión para la energía cinética de la física el concepto de trabajo
o Entender la relación de trabajo y energía cinética
o Calcular la energía cinética de diversos objetos
Vamos a Empezar!
Relacionar el trabajo y la Energía Cinética
En cierto sentido, el trabajo es la cantidad de energía puesta en una tarea (o, quizás, «puesta en el objeto»). Por ejemplo, imagine que levantamos un objeto del suelo y lo elevamos a una cierta altura; hemos trabajado mucho en ese objeto. Sin embargo, si lo dejamos ir, se acelera, como si el trabajo que hicimos al levantar el objeto se convirtiera en movimiento. A través de este ejemplo, podemos derivar una definición de energía cinética, que es energía de movimiento. Esta definición, como veremos, está estrechamente relacionada con la forma en que hemos definido el trabajo.
En primer lugar, consideremos un objeto: una bola de masa m. Recogeremos la bola de una mesa y la elevaremos a una distancia h por encima de esa mesa, como se muestra a continuación. Por lo tanto, hemos hecho una cantidad de trabajo W = mgh, (este resultado es el producto de la magnitud del vector de desplazamiento (h) y la fuerza aplicada (mg) the los vectores correspondientes son paralelos).
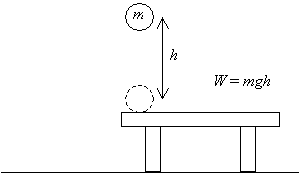
Ahora, si soltamos esa bola y la dejamos caer desde la altura h sobre la mesa, una vez que vuelva a su altura original (el nivel de la mesa), tendrá una cierta velocidad v resultante de la aceleración debida a la gravedad.
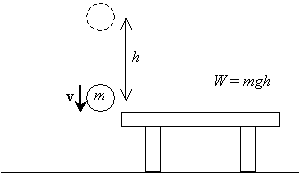
Queremos calcular esta velocidad (o velocidad, técnicamente may ocasionalmente podemos sustituir el término velocidad por velocidad, pero siempre seamos conscientes de que la velocidad es en realidad un vector y la velocidad es la magnitud de la velocidad). Sabemos que la aceleración debida a la gravedad es constante, y que la velocidad inicial de la pelota es cero (es estacionaria antes de que se publique). Asumiremos que la altura inicial de la bola es h y que su altura final es cero (el nivel de la mesa). Para calcular la velocidad derivando las fórmulas apropiadas, se requiere el uso de cálculo integral elemental. (Si usted es un estudiante avanzado o está buscando un desafío adicional, puede intentar derivar estas fórmulas bajo las condiciones anteriores usted mismo. Simplemente tenga en cuenta que la velocidad v de la bola es la tasa de tiempo de cambio de su posición x en función del tiempo t, ![]() , y que la aceleración a es la tasa de tiempo de cambio de la velocidad,
, y que la aceleración a es la tasa de tiempo de cambio de la velocidad, ![]() .)
.)
![]()
![]()
Estas fórmulas expresan la velocidad en función del tiempo, v (t), y la posición (altura) en función del tiempo, x(t), en términos de la aceleración a, altura h y tiempo t. Sabemos que a = –g, ya que la bola solo se acelera por gravedad y esta aceleración es hacia abajo (de ahí el signo negativo). La posición final de la bola es de cero metros, o x(t) = 0. Calculemos t, la cantidad de tiempo entre el lanzamiento de la bola y su llegada al nivel de la mesa.
![]()
![]()
![]()
Ahora, vamos a calcular la velocidad de la pelota en este momento.
![]()
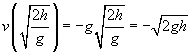
Ahora comparemos este resultado con el trabajo realizado originalmente en el objeto: W = mgh. Observe lo cerca que están en forma estas dos expresiones; de hecho, el único factor que falta en la velocidad es la masa de la bola, m. Si cuadráramos la velocidad, multiplicada por m, y luego dividida por 2, ¡de hecho tendríamos la misma expresión que la obra!
![]()
Por lo tanto, podemos ver en cierto sentido cómo se puede derivar la definición de energía cinética. La energía cinética K de un objeto, entonces, es un escalar definido de la siguiente manera, donde m es la masa del objeto y v es su velocidad:
![]()
Resulta que la energía cinética es el trabajo realizado en un objeto por la fuerza neta en ese objeto. Por lo tanto, aunque una mujer puede hacer una cierta cantidad de trabajo en un objeto levantándolo de una altura a otra, la fuerza neta en ese objeto es cero (la mujer aplica una fuerza igual pero opuesta en la dirección de la gravedad). Por lo tanto, no hay cambio en la energía cinética. Sin embargo, si ese objeto se libera y se le permite caer, gana energía cinética porque la fuerza neta sobre él es simplemente la de la gravedad (una sola fuerza). Por lo tanto, para entender la relación de la energía cinética y el trabajo, debemos refinar un poco nuestro concepto de trabajo. Si definimos el trabajo W como el trabajo total realizado en el objeto por todas las fuerzas (en otras palabras, el trabajo realizado en el objeto por la fuerza neta), entonces se mantiene la siguiente relación entre el trabajo W y las energías cinéticas inicial y final (Ki y Kf).
![]() donde
donde ![]()
Por lo tanto, el trabajo neto realizado en un objeto es igual al cambio en la energía cinética de ese objeto (ΔK). Los siguientes problemas de práctica le brindan la oportunidad de probar y aplicar su comprensión de los conceptos de trabajo y energía cinética.
Problema de práctica: Un proyectil de masa de 1 kilogramo viaja a 5 metros por segundo. ¿A qué velocidad debe viajar un proyectil de 0,1 kilogramos para lograr la misma energía cinética?
Solución: En primer lugar, calculemos la energía cinética del proyectil más masivo (1 kilogramo).
![]()
Ahora podemos calcular la velocidad del objeto menos masivo de modo que tenga la misma energía cinética, K.
![]()
![]()
![]()
Problema de práctica: Un hombre levanta un peso de 15 kilogramos a una altura de dos metros del suelo antes de dejarlo caer. En el instante antes de que el peso entre en contacto con el suelo, ¿cuál es su velocidad?
Solución: Dibujemos un diagrama que ilustre las fuerzas que actúan sobre el objeto a medida que se levanta y cae; estas fuerzas incluyen la gravedad (Fg) y la fuerza ascendente que aplica el hombre (Fu).
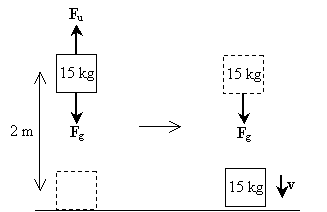
Tenga en cuenta que el primer paso del proceso (levantar el peso) no implica una fuerza neta que actúe sobre el objeto: la fuerza debida a la gravedad se equilibra con la fuerza que el hombre aplica al levantar el peso. En el segundo paso, sin embargo, el peso solo experimenta la fuerza de la gravedad. La fuerza neta, en este caso, es por lo tanto mg en la dirección descendente. Como tal, la velocidad del objeto también está en la dirección descendente. El trabajo realizado en el peso como resultado de la gravedad es simplemente mgh; este es también el trabajo total realizado en el peso a lo largo del proceso. Tenga en cuenta que la energía cinética inicial del peso es cero porque tiene velocidad cero. Calculemos ahora la velocidad aplicando la relación entre el trabajo neto y el cambio en la energía cinética.