liike-energia on liike-energiaa. Liike-energiaa kuvaava lauseke saadaan tarkastelemalla tapausta, jossa kappale nostetaan johonkin suhteelliseen korkeuteen (näin tälle kappaleelle tehdään työtä) ja sen annetaan sitten pudota.
keskeiset termit
o kineettinen energia
tavoitteet
o johtaa lauseke liike-energialle työn fysiikan käsitteestä
O ymmärrä työn ja liike-energian suhde
O laske eri kappaleiden liike-energia
aloitetaan!
liittyvät työt ja liike-energia
jossain mielessä työ on tehtävään (tai ehkä ”kohteeseen”) laitetun energian määrä. Kuvittele esimerkiksi, että nostamme jonkin esineen lattialta ja nostamme sen tietylle korkeudelle.; olemme tehneet jonkin verran työtä sen kohteen eteen. Mutta jos annamme sen mennä, se kiihtyy, ikään kuin se työ, jonka teimme nostaessamme esinettä, muuttuisi liikkeeksi. Tämän esimerkin avulla voimme johtaa määritelmän liike-energialle, joka on liike-energia. Tämä määritelmä, kuten tulemme näkemään, liittyy läheisesti siihen, miten olemme määritelleet työn.
tarkastellaan ensin kohdetta: palloa, jonka massa on m.poimimme pallon pöydältä ja nostamme sen etäisyyden h kyseisen pöydän yläpuolelle, kuten alla on esitetty. Olemme siis tehneet paljon työtä W = mgh, (tämä tulos on tulo suuruus Siirtymä vektori (h) ja sovellettu voima (mg) – vastaavat vektorit ovat yhdensuuntaisia).
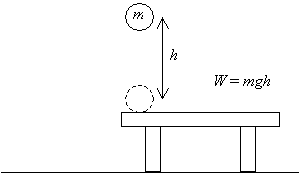
nyt, jos vapautamme pallon ja annamme sen pudota korkeudesta h pöydän yläpuolella, kun se palaa alkuperäiseen korkeuteensa (taulukon tasolle), sillä on tietty nopeus v, joka johtuu painovoiman aiheuttamasta kiihtyvyydestä.
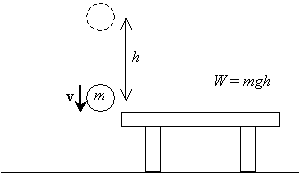
haluamme laskea tämän nopeuden (tai nopeuden, teknisesti-voimme joskus korvata termi nopeus nopeuden, mutta aina olla tietoinen siitä, että nopeus on itse asiassa vektori ja nopeus on suuruus nopeus). Tiedämme, että painovoiman aiheuttama kiihtyvyys on vakio ja että pallon alkunopeus on nolla (se on paikallaan ennen kuin se vapautuu). Oletamme, että pallon aloituskorkeus on h ja että sen lopullinen korkeus on nolla (taulukon taso). Laskea nopeus johtamalla asianmukaiset kaavat, tarvitsemme käytön alkeisintegraali calculus. (Jos olet edistynyt opiskelija tai etsit ylimääräistä haastetta, voit kokeilla näiden kaavojen johtamista edellä mainituissa olosuhteissa itse. Huomaa vain, että pallon nopeus v on sen sijainnin X muuttumisen aikanopeus ajan t funktiona, ![]() , ja että kiihtyvyys a on nopeuden muutoksen aikanopeus,
, ja että kiihtyvyys a on nopeuden muutoksen aikanopeus, ![]() .)
.)
![]()
![]()
nämä kaavat ilmaisevat nopeuden ajan funktiona v (t) ja paikan(korkeus) ajan funktiona x (t) kiihtyvyyden a, korkeuden h ja ajan t suhteen. tiedämme, että A = –g, koska kuulaa kiihdyttää vain painovoima ja tämä kiihtyvyys on alaspäin (tästä negatiivinen merkki). Pallon lopullinen sijainti on nolla metriä eli x (t) = 0. Lasketaan t, aika pallon vapautumisen ja sen saapumisen välillä taulukon tasolla.
![]()
![]()
![]()
lasketaan pallon nopeus tällä hetkellä.
![]()
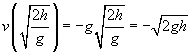
Verratkaamme nyt tätä tulosta kohteeseen alun perin tehtyyn työhön: W = mgh. Huomaa, kuinka lähellä muodossa nämä kaksi lauseketta ovat; itse asiassa ainoa tekijä puuttuu nopeus on massa pallo, m. Jos me neliöidään nopeus, kerrottuna m, ja sitten jaettu 2, meillä olisi itse asiassa sama ilmaus kuin työ!
![]()
näin voimme nähdä jossain mielessä, miten kineettisen energian määritelmä voidaan johtaa. Kappaleen liike-energia K on siis skalaari, joka määritellään seuraavasti, missä m on kappaleen massa ja v on sen nopeus:
![]()
kuten käy ilmi, liike-energia on työtä, joka tehdään objektin nettovoima, että objekti. Vaikka siis nainen voi tehdä tietyn määrän työtä esineelle nostamalla sitä korkeudesta toiseen, nettovoima esineeseen on nolla (nainen käyttää painovoiman suunnassa yhtä suurta mutta vastakkaista voimaa). Liike-energiassa ei siis tapahdu muutosta. Jos kappale kuitenkin vapautuu ja sen annetaan pudota, se saa liike-energiaa, koska siihen kohdistuva nettovoima on yksinkertaisesti gravitaation voima (yksittäinen voima). Jotta siis ymmärtäisimme liike-energian ja työn suhdetta, meidän on tarkennettava käsitystämme työstä jonkin verran. Jos määrittelemme työn W kaikkien voimien kokonaisuudeksi objektille tekemäksi työksi (toisin sanoen nettovoiman kohteelle tekemäksi työksi), niin seuraava työn W ja alku-ja loppumineettisten energioiden (Ki ja Kf) välinen suhde pätee.
![]() jos
jos ![]()
näin kappaleelle tehty nettotyö on yhtä suuri kuin kyseisen kappaleen liike-energian (ΔK) muutos. Seuraavat käytännön ongelmat antavat sinulle mahdollisuuden testata ja soveltaa ymmärrystäsi työn ja liike-energian käsitteistä.
Käytännön Ongelma: Yhden kilogramman massainen ammus kulkee 5 metriä sekunnissa. Millä nopeudella 0,1 kilogramman ammuksen on kuljettava saavuttaakseen saman liike-energian?
ratkaisu: lasketaan ensin massiivisemman (1 kilogramman) ammuksen liike-energia.
![]()
voimme nyt laskea vähemmän massiivisen kappaleen nopeuden siten, että sillä on tämä sama liike-energia, K.
![]()
![]()
![]()
Harjoitusongelma: mies nostaa 15 kilon painon kahden metrin korkeuteen maasta ennen pudottamistaan. Mikä on sen nopeus ennen kuin paino koskettaa maata?
ratkaisu: piirretään kaavio, joka havainnollistaa kappaleeseen sen nostaessa ja pudotessa vaikuttavia voimia; näitä voimia ovat painovoima (Fg) ja ihmisen kohdistama ylöspäin suuntautuva voima (Fu).
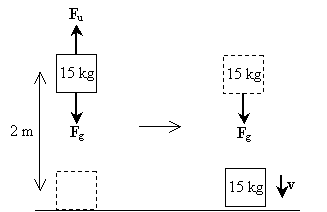
huomaa, että prosessin ensimmäinen vaihe (painon nostaminen) ei sisällä esineeseen vaikuttavaa nettovoimaa-painovoiman aiheuttamaa voimaa tasapainottaa voima, jota ihminen soveltaa painon nostamiseen. Toisessa vaiheessa paino kuitenkin kokee vain painovoiman. Nettovoima on tässä tapauksessa siis mg alaspäin. Sellaisena kappaleen nopeus on myös alaspäin suuntautuvassa suunnassa. Painoon painovoiman seurauksena tehty työ on yksinkertaisesti mgh; tämä on myös koko painolle tehty työ koko prosessin ajan. Huomaa, että painon alkuperäinen liike-energia on nolla, koska sen nopeus on nolla. Lasketaan nyt nopeus soveltamalla nettotyön ja liike-energian muutoksen suhdetta.