Data Science from the ground up
building an intuition for how KNN models work
Data science or applied statistics courses typically started with linear models, but in its way, K-neighbors is probably the simplestly widely used model conceptually. KNN-mallit ovat oikeastaan vain teknisiä toteutuksia yhteisestä intuitiosta, että asiat, joilla on samanlaisia ominaisuuksia, ovat yleensä, no, samanlaisia. Tämä on tuskin syvä oivallus, mutta nämä käytännön toteutukset voivat olla erittäin tehokas, ja, mikä on ratkaisevaa, että joku lähestyy tuntematon tietokokonaisuus, voi käsitellä ei-lineaarisuus ilman monimutkaisia data-engineering tai malli perustettu.
mitä
havainnollistavana esimerkkinä tarkastellaan yksinkertaisinta tapausta KNN-mallin käyttämisestä luokittelijana. Oletetaan, että sinulla on datapisteitä, jotka kuuluvat yhteen kolmesta luokasta. Kaksiulotteinen esimerkki voi näyttää tältä:

voit luultavasti nähdä melko selvästi, että eri luokat on ryhmitelty yhteen — kuvaajien vasen yläkulma näyttää kuuluvan oranssiin luokkaan, oikea/keskiosa siniseen luokkaan. Jos sinulle annettaisiin uuden pisteen koordinaatit jossain kaaviossa ja kysyttäisiin, mihin luokkaan se todennäköisesti kuuluisi, vastaus olisi useimmiten melko selvä. Mikä tahansa piste kuvaajan vasemmassa yläkulmassa on todennäköisesti oranssi jne.
tehtävä muuttuu kuitenkin hieman epävarmemmaksi luokkien välissä, jossa joudutaan asettumaan ratkaisurajalle. Harkitse uusi kohta lisätty punaisella alla:

pitäisikö tämä uusi piste luokitella oranssiksi vai siniseksi? Piste näyttää jäävän kahden ryppään väliin. Ensimmäinen intuitiosi voi olla valita klusteri, joka on lähempänä uutta pistettä. Tämä olisi ”lähin naapuri” lähestymistapa, ja vaikka käsitteellisesti yksinkertainen, se usein tuottaa melko järkeviä ennusteita. Mikä aiemmin tunnistettu piste on lähin uusi piste? Se ei ehkä ole selvää vain silmäilemällä graafi, mikä vastaus on, mutta se on helppo tietokone ajaa läpi pistettä ja antaa meille vastauksen:

, näyttää siltä, että lähin piste on sinisessä kategoriassa, joten Uusi pistekin on todennäköisesti myös. Se on lähimmän naapurin menetelmä.
tässä vaiheessa voi ihmetellä, mitä varten K-lähinaapurin K-kirjain on. K on läheisten pisteiden lukumäärä, jota malli tarkastelee arvioidessaan uutta pistettä. Meidän yksinkertaisin lähin naapuri esimerkki, tämä arvo k oli yksinkertaisesti 1 – katsoimme lähin naapuri ja se oli se. Olisit kuitenkin voinut valita lähimmän 2 tai 3 pistettä. Miksi tämä on tärkeää ja miksi joku asettaisi k: n suurempaan lukuun? Ensinnäkin luokkien väliset rajat saattavat törmätä toisiinsa tavoilla, jotka tekevät vähemmän ilmeiseksi sen, että lähin piste antaa meille oikean luokittelun. Tarkastellaan sinistä ja vihreää aluetta esimerkissämme. Itse asiassa, zoomataan niihin.:

huomaa, että vaikka kokonaisalueet näyttävät riittävän erillisiltä, niiden rajat näyttävät hieman kietoutuvan toisiinsa. Tämä on yleinen piirre datajoukoissa, joissa on vähän melua. Kun näin on, raja-alueiden asioiden luokittelu vaikeutuu. Harkitse tätä uutta seikkaa:

toisaalta, visuaalisesti näyttää varmasti siltä, että lähin aiemmin tunnistettu piste on sininen, jonka tietokoneemme voi helposti vahvistaa meille:

toisaalta, että lähin sininen piste vaikuttaa itse hieman ulkopuoliselta, kaukana sinisen alueen keskustasta ja tavallaan vihreiden pisteiden ympäröimältä. Ja tämä uusi piste on jopa tuon sinisen pisteen ulkopuolella! Mitä jos katsoisimme kolmea lähintä pistettä uudesta punaisesta pisteestä?

vai edes lähintä viittä pistettä uuteen pisteeseen?

, nyt näyttää siltä, että uusi pisteemme on vihreässä naapurustossa! Sillä sattui olemaan lähellä sininen piste, mutta preponderance tai läheiset pisteet ovat vihreitä. Tässä tapauksessa, ehkä olisi järkevää asettaa korkeampi arvo k, tarkastella kourallinen lähellä pistettä ja saada heidät äänestämään jotenkin ennuste uuden pisteen.
kuvitettu aihe on yliampuva. Kun k asetetaan ykköseksi, raja, jonka alueet algoritmi tunnistaa siniseksi ja vihreäksi, on kuoppainen, se kiemurtelee edestakaisin jokaisen yksittäisen pisteen kanssa. Punainen piste näyttää siltä, että se voisi olla sinisellä alueella:

tuoden k: n jopa 5: een, kuitenkin tasoittaa ratkaisurajaa läheisten pisteiden äänestäessä. Punainen piste näyttää nyt tukevasti vihreältä naapurustolta:

kauppa pois K: n korkeammilla arvoilla on rakeisuuden menetys päätösrajassa. K: n asettaminen hyvin korkealle antaa sinulle yleensä sileät rajat, mutta todellisen maailman rajat, joita yrität mallintaa, eivät välttämättä ole täysin sileät.
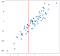
käytännössä voidaan käyttää samantyyppistä lähimmät naapurit-lähestymistapaa regressioihin, jossa haluamme yksilöllisen arvon luokituksen sijaan. Tarkastellaan seuraavaa regressiota alla:

aineisto luotiin satunnaisesti, mutta se luotiin lineaariseksi, joten lineaarinen regressiomalli sopisi luonnollisesti hyvin tähän aineistoon. Haluan kuitenkin huomauttaa, että lineaarisen menetelmän tuloksia voi lähentää käsitteellisesti yksinkertaisemmalla tavalla k-lähimmät naapurit-lähestymistavalla. Meidän ’regressio’ tässä tapauksessa ei ole yksi kaava kuin OLS malli antaisi meille, vaan parhaiten ennustettu lähtöarvo tahansa syötteen. Harkitse arvo -.75 x-akselilla, jonka olen merkinnyt pystyviivalla:

ratkaisematta mitään yhtälöitä voimme tulla kohtuulliseen lähentämisestä, mitä tuotos olisi vain tarkastelemalla lähellä pistettä:

on järkevää, että ennustettu arvo on lähellä näitä pisteitä, ei paljon pienempi tai korkeampi. Ehkä hyvä ennuste olisi näiden pisteiden keskiarvo:
voi kuvitella tekevänsä näin kaikille mahdollisille tuloarvoille ja keksivänsä ennusteita kaikkialla:

kaikkien näiden ennusteiden yhdistäminen viivaan antaa meille regressiomme:

tässä tapauksessa tulokset eivät ole puhdas viiva, mutta ne kyllä jäljittävät datan nousukiitoa kohtuullisen hyvin. Tämä ei ehkä tunnu kauhean vaikuttavalta, mutta yksi hyöty tämän toteutuksen yksinkertaisuudesta on se, että se käsittelee epälineaarisuutta hyvin. Harkitse tätä uutta pisteiden kokoelmaa:
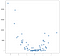
nämä pisteet syntyivät yksinkertaisesti neliöimällä edellisen esimerkin arvot, mutta oletetaan, että törmäät tällaiseen aineistoon luonnossa. Se ei ilmeisesti ole lineaarinen luonteeltaan ja vaikka OLS-tyylinen malli voi helposti käsitellä tällaista dataa, se vaatii epälineaaristen tai vuorovaikutustermien käyttöä, eli data scientist on tehtävä joitakin päätöksiä siitä, minkälaista tietotekniikkaa suorittamaan. KNN: n lähestymistapa ei vaadi uusia päätöksiä — lineaariesimerkin käyttämää koodia voidaan käyttää uudelleen kokonaan uudessa datassa, jolloin saadaan toimiva ennustejoukko:

kuten luokittajan esimerkeissä, suuremman arvon k asettaminen auttaa meitä välttämään ylilyöntejä, vaikka saatat alkaa menettää ennakoivaa valtaa marginaalissa, erityisesti datajoukkosi reunoilla. Harkitse ensimmäinen esimerkki dataset kanssa ennusteita k asetettu yksi, joka on lähin naapuri lähestymistapa:

ennusteemme hyppäävät arvaamattomasti mallin hypätessä datajoukon yhdestä pisteestä toiseen. Sitä vastoin K: n asettaminen kymmeneen, niin että kymmenen kokonaispistettä lasketaan yhteen keskimäärin ennustamista varten, tuottaa paljon tasaisempaa kyytiä.:

yleensä se näyttää paremmalta, mutta voit nähdä jotain ongelma reunoilla tietoja. Koska mallimme ottaa niin monta pistettä huomioon mitä tahansa ennustetta varten, kun pääsemme lähemmäksi yhtä otoksemme reunoista, ennusteemme alkavat huonontua. Voimme käsitellä tätä asiaa jonkin verran painottamalla ennusteitamme lähempänä oleviin kohtiin, vaikka tähän liittyy omat kauppansa.
miten
KNN-mallia määritettäessä on vain kourallinen parametreja, jotka on valittava/joita voidaan säätää suorituskyvyn parantamiseksi.
k: naapureiden lukumäärä: Kuten on keskusteltu, K: n lisääminen pyrkii tasoittamaan päätöksenteon rajoja välttäen ylilyöntejä jonkin ratkaisun kustannuksella. Ei ole yhtä arvoa k, joka toimisi joka ikinen aineisto. Luokittelumalleissa, varsinkin jos luokkia on vain kaksi, valitaan yleensä pariton luku K: lle. tämä on niin, että algoritmi ei koskaan joudu ”tasapeliin”: esimerkiksi se katsoo neljää lähintä pistettä ja toteaa, että kaksi niistä on sinisessä luokassa ja kaksi punaisessa luokassa.
etäisyysmittari: On, kuten on käynyt ilmi, erilaisia tapoja mitata, kuinka ”lähellä” kaksi pistettä ovat toisiaan, ja erot näiden menetelmien voi tulla merkittäviä korkeampien ulottuvuuksien. Yleisimmin käytetty on Euklidinen etäisyys, standardilaji, jonka olet saattanut oppia keskikoulussa Pythagoraan lausetta käyttäen. Toinen metriikka on niin sanottu ”Manhattanin etäisyys”, joka mittaa kussakin kardinaalisessa suunnassa otettua etäisyyttä lävistäjän sijaan (ikään kuin kävelisit Manhattanin katujen risteyksestä toiseen ja joutuisit seuraamaan katuverkkoa sen sijaan, että olisit voinut valita lyhimmän ”linnuntietä” – reitin). Yleisemmin nämä ovat itse asiassa molemmat niin sanotun ”Minkowskin etäisyyden” muodot, joiden kaava on:

kun p on asetettu arvoon 1, Tämä kaava on sama kuin Manhattanin Etäisyys, ja kun asetettu arvoon kaksi, Euklidinen etäisyys.
painot: yksi tapa ratkaista sekä kysymys mahdollisesta ”tasapelistä”, kun algoritmi äänestää luokkaa, että kysymys, jossa regressioennustuksemme huononivat aineiston reunoja kohti, on ottaa käyttöön painotus. Painoilla lähipisteitä lasketaan enemmän kuin kauempana olevia pisteitä. Algoritmi katsoo vielä kaikki K lähimmät naapurit, mutta lähimmillä naapureilla on enemmän ääntä kuin kauempana olevilla. Tämä ei ole täydellinen ratkaisu ja tuo esiin mahdollisuuden ylilataukseen uudelleen. Harkitse regressioesimerkkiä, tällä kertaa painoilla:

ennusteemme menevät nyt aivan datajoukon reunalle, mutta voit nähdä, että ennusteemme heilahtavat nyt paljon lähemmäs yksittäisiä pisteitä. Painotettu menetelmä toimii kohtuullisen hyvin, kun olet pisteiden välissä, mutta kun tulet lähemmäksi ja lähemmäksi jotakin tiettyä pistettä, kyseisen pisteen arvo vaikuttaa yhä enemmän algoritmin ennustamiseen. Jos pääset tarpeeksi lähelle pistettä, se on melkein kuin asettaisi k: n yhteen, koska sillä pisteellä on niin paljon vaikutusvaltaa.
skaalaus/normalisointi: viimeinen, mutta ratkaisevan tärkeä seikka on se, että KNN-mallit voidaan heittää pois, jos eri ominaisuusmuuttujilla on hyvin erilaiset asteikot. Harkitse mallia,joka yrittää ennustaa vaikkapa talon myyntihinnan markkinoilla perustuen ominaisuuksiin, kuten makuuhuoneiden määrään ja talon kokonaisneliömateriaaliin jne. Talon neliömäärässä on enemmän vaihtelua kuin makuuhuoneiden määrässä. Tyypillisesti taloissa on vain pieni kourallinen makuuhuoneita, eikä edes suurimmassa kartanossa tule olemaan kymmeniä tai satoja makuuhuoneita. Neliöjalat taas ovat suhteellisen pieniä, joten talot saattavat vaihdella pienellä puolella lähes 1000 neliömetrin suuruisista kymmeniin tuhansiin neliöjalkoihin.
harkitse vertailua 2 000 neliön jalkataloon, jossa on 2 makuuhuonetta, ja 2 010 neliön jalkataloon, jossa on kaksi makuuhuonetta — 10 neliömetriä. jaloilla ei ole väliä. Sen sijaan 2000 neliön talo, jossa on kolme makuuhuonetta, on hyvin erilainen, ja edustaa hyvin erilaista ja mahdollisesti ahtaampaa ulkoasua. Naiivi tietokone ei olisi yhteydessä ymmärtää, että, kuitenkin. Se sanoisi, että 3 makuuhuone on vain ”yhden” yksikön päässä 2 Makuuhuone, kun taas 2,010 sq alatunniste on ”kymmenen” päässä 2,000 sq alatunniste. Tämän välttämiseksi ominaisuustiedot on skaalattava ennen KNN-mallin käyttöönottoa.
vahvuudet ja heikkoudet
KNN-mallit on helppo toteuttaa ja käsitellä epälineaarisuuksia hyvin. Mallin sovittaminen on myös nopeaa: tietokoneen ei tarvitse loppujen lopuksi laskea mitään tiettyjä parametreja tai arvoja. Kauppa pois tässä on, että vaikka malli on nopea perustaa,se on hitaampaa ennustaa, koska voidakseen ennustaa tuloksen uuden arvon, se täytyy etsiä läpi kaikki kohdat sen koulutus asettaa löytää lähimmät. Suurille tietokokonaisuuksille KNN voi siis olla suhteellisen hidas menetelmä verrattuna muihin regressioihin, joiden sovittaminen voi kestää kauemmin, mutta jotka sitten tekevät ennusteensa suhteellisen suoraviivaisilla laskutoimituksilla.
toinen KNN-mallin ongelma on se, että siitä puuttuu tulkinnanvaraisuus. OLS-lineaarinen regressio on selvästi tulkittavissa kertoimia, jotka voivat itsessään antaa joitakin viitteitä ”vaikutus koko” tietyn ominaisuuden (vaikka, joitakin varovaisuutta on noudatettava, kun osoitetaan syy-yhteys). KNN-mallin kannalta ei kuitenkaan ole järkevää kysyä, millä ominaisuuksilla on suurin vaikutus. Osittain tämän vuoksi KNN-malleja ei myöskään voida käyttää ominaisuuksien valintaan, kuten lineaarinen regressio lisäkustannusfunktion termillä, kuten ridge tai lasso, tai tapa, jolla päätöksentekopuu implisiittisesti valitsee, mitkä ominaisuudet vaikuttavat arvokkaimmilta.