tietorakenne

poimittu oppikoulujen luonnontieteen opettajien Työpajan mukana olevasta vihkosesta.

Robert J. Dufresne, William J. Leonard ja William J. Gerace

ryhmämme Umassissa on kehittänyt kognitiivisen mallin, joka auttaa meitä edustamaan eroja siinä, miten asiantuntijat ja aloittelijat tallentavat ja käyttävät sisältötietämystä. Malli auttaa meitä myös kohdentamaan tiettyjä aloja, joihin aloittelijoiden on keskityttävä tullakseen paremmiksi ongelmanratkaisijoiksi. Malli on kuitenkin vain yksi tiedon rakenteen esitys, ja se kehittyy jatkuvasti. Siksi sitä ei saa ottaa liian kirjaimellisesti. Sen hyödyllisyys johtuu sen kyvystä antaa konkreettinen osoitus siitä, miten asiantuntijat ja aloittelijat ajattelevat, vaikkakin epätäydellisesti. Malli auttaa keskustelemaan:

1. toimialakohtaisen tiedon tallennus;
2. asiantuntija-ja aloittelijamainen ongelmanratkaisukäyttäytyminen;
3. asiantuntijan tietovaraston hierarkkinen rakenne;
4. harhaluulot;
5. päämäärättömien ja tavoitteellisten kysymysten vaikutukset; ja
6. metaviestintäprosessi.

tässä työpajassa- – – ja lähestymistavassamme fysiikkaan yleensä – – – on 3 perusteemaa:

1. taitavaan ongelmanratkaisuun tarvitaan tietyntyyppisiä tietoja ja tietorakenteita. Suuri osa tästä tiedosta on luonteeltaan käsitteellistä, toisin kuin operatiivinen tai proseduraalinen, ja voimakkaisiin tietorakenteisiin liittyy väistämättä käsitteellisiä elementtejä. Käsitteellisten elementtien läsnäolo tietorakenteissa on avain fysiikan ”syvempään ymmärtämiseen”.
2. käsitteellisen tiedon hankkimiseen ja hyödyllisten tietorakenteiden rakentamiseen tarvitaan tietyntyyppisiä kognitiivisia prosesseja.
3. on mahdollista suunnitella toimintoja, jotka edistävät näitä toivottavia kognitiivisia prosesseja. Monissa tapauksissa nämä toiminnot ovat vain itse kognitiivisten prosessien aktuaalistumia. (Tämä kohta selkiytyy toivottavasti myöhemmin.)

käsittelemme kutakin näistä aiheista tarkemmin ennen kuin keskitymme erityisiin esimerkkeihin.

Teema 1: Mitä opiskelijoiden tulee tietää ja miten heidän tietonsa tulisi jäsentää tehokkaan ongelmanratkaisun aikaansaamiseksi?

aloitamme tunnistamalla joitakin erityyppisiä tietoja, jotka opiskelijoiden tulee tietää:

• käsitteellinen tieto, kuten liikemäärän tai energian käsite, tai että kappaleen nopeus muuttuu sen kiihtyessä, tai että kappaleen gravitaatiopotentiaalienergia pienenee sen pudotessa.
• faktatietoa, kuten gravitaatiovakion g arvo, Kuun säde tai raudan tiheys.
• esitystaito, kuten kaavioiden piirtäminen ja käyttö.
• strateginen tietämys, kuten kyky tunnistaa jonkin käsitteen sovellettavuus, kuten liikemäärä säilyy, kun ulkoisia voimia ei ole, tai että energia säilyy, kun ei-konservatiivisia voimia ei ole.
• Metakognitiivista tietoa, esimerkiksi tietoisuus taustalla olevista oletuksista, tai että vastaus tulisi tarkistaa ratkaisemalla ongelma toisella tavalla.
• itsetuntemus, kuten omien todennäköisten virheiden lähteiden tunteminen tai tieto siitä, että ongelmia ratkoessa pitäisi olla menettelyllisempi.
• operatiivinen tieto, kuten miten otetaan kahden vektorin ristitulo tai pistetulo, tai miten otetaan matriisin determinantti tai miten piirretään vapaakappalekaavio.
• prosessitiedot, kuten milloin energiansäästöä käytetään (ts., kun kaikki voimat ovat konservatiivisia), tai milloin määritetään koordinaatisto (esim.potentiaalienergiaa löydettäessä), tai milloin piirretään vapaan kappaleen Diagrammi (esim. Newtonin lakeja sovellettaessa).
• Ongelmatilatuntemus, joita käytetään ratkaistaessa ongelman ratkaisua. Esimerkkejä ovat: tietäen, että tietyssä ongelmassa ei ole ulkoisia voimia, tai että ongelmassa ei ole ei-konservatiivisia voimia, tai että objekti on aluksi levossa tai että objekti on kaltevuudessa.

tämäntyyppiset tiedot on järjestettävä ja jäsenneltävä, jotta niitä voidaan käyttää tehokkaasti ongelmanratkaisussa. Voidaksemme keskustella tiedon organisatorisista ja rakenteellisista näkökohdista olemme havainneet sopivaksi luokitella nämä tyypit kolmeen yleiseen kategoriaan. Kutsumme näitä kolmea ryhmää: käsitteellinen tieto, operatiivinen ja menettelyllinen tieto sekä Ongelmatilatieto. Kuvassa. 1, Nämä kolme yleistä kategoriaa näkyvät esityksessä siitä, miten asiantuntijat tallentavat sisältötietämystä.

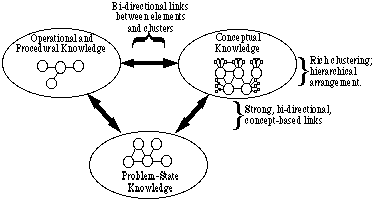Kuva. 1: Representaatio asiantuntijan tietorakenteesta

asiantuntijalla on runsas käsitteistö, jossa jokainen käsite liittyy moniin muihin käsitteisiin ja käsitteiden väliset suhteet ymmärretään selvästi. Käsitteet on järjestetty hierarkkisesti sateenvarjokäsitteiden avulla niiden tiiviimmäksi suhteuttamiseksi. Itse asiassa, sateenvarjo käsitteitä käytetään ryhmitellä elementtejä kunkin kolmen kategorian. Asiantuntijalla on runsaasti ongelmatilanteiden tuntemusta, mukaan lukien paljon tietoa siitä, mitkä periaatteet pätevät erityistilanteissa. Asiantuntija on myös suuri varasto yhtälöt, toiminnot, ja menettelyt (EOPs), joka voidaan nopeasti.

kunkin kategoriaparin väliset yhteydet ovat hyvin vahvat: ongelmatilat liittyvät vahvasti käsitteisiin ja EOPs: iin, jotka itse ovat vahvasti sidoksissa toisiinsa. Samoilla sateenvarjokäsitteillä ryhmitellään käsitteet, ongelmatilat ja EOPs. Siksi minkä tahansa tietyn ongelman osalta käsitteitä voidaan käyttää päättämään yhtälöiden asianmukaisuudesta ja sovellettavuudesta sekä erityisten toimien ja menettelyjen hyödyllisyydestä.

(Tässä täytyy olla hyvin varovainen, ettei ole liian jäykkä omassa ajattelussaan, koska on helppo olla eri mieltä siitä, mitä näistä kategorioista pitäisi käyttää tietyn tiedon elementin luokitteluun, vai kuuluuko se vain yhteen kategoriaan. Tarkoituksemme on vain saada mekanismi visualisoida useita tasoja assosiaatio, joka voi tapahtua elementtien välillä.)

meillä on tapana käyttää termiä linkitys tarkoittamaan kahden saman tai eri tietotyypin elementin muodostunutta assosiaatiota, ja termiä klusterointi viittaamaan useiden elementtien tai klustereiden välisiin assosiaatioihin. Tällaisen keskustelun tekee hyvin vaikeaksi se, että tässä on meneillään eräänlainen iteratiivinen prosessi.: Erittäin vahva side kolmen kohteen—käsitteellisen klusterin, käsitteen soveltamiseen tarvittavien olosuhteiden ja sen soveltamiseen tarvittavien menettelyjen tunnustamisen välillä – – – muodostaa uudenlaisen tietoelementin, jonka panemme strategiseen tietoon (neljäs kategoria). Tämä uusi tietoelementti on se, mitä jotkut kutsuvat skeemaksi, ja siihen liittyy usein myös ongelmatilatietoa. Koska tietoelementti on luonteeltaan käsitteellinen, se monistuu (eli toistuu) käsitteellisessä kuplassa.

jos tarkastelemme tarkemmin käsitteellistä kuplaa, näemme joitakin käsitteellisen tiedon erityistyyppejä, esimerkiksi edustavaa tietoa, strategista tietoa, Metakognitiivista tietoa ja tietoa peruskäsitteistä. Tämä on esitetty kuvassa. 2. (Muunlaista käsitteellistä tietoa ei esitetä.)

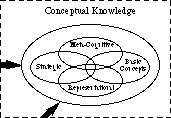Kuva. 2: käsitteellisen tiedon tyypit

miten noviisin tietorakenne eroaa asiantuntijan tietorakenteesta? Kuten esitetty kuvassa. 3, aloittelijat ovat yleensä huono klusterointi käsitteitä. Monet linkit ovat sopimattomia, toiset olemattomia. Osa sopimattomista linkeistä on erittäin vahvoja, mikä johtaa väärinkäsityksiin. Noviisit eivät yleensä käytä sateenvarjokonsepteja ryhmitelläkseen elementtejä. Heillä on pieni varasto ongelmatilanteita, joissa pinnan ominaisuuksia käytetään niputtamaan ne yhteen ja päättämään, miten ongelmat pitäisi ratkaista. He tuntevat suhteellisen suuren määrän yhtälöitä, mutta he muistavat ne usein väärin tai tarvitsevat etsiä niitä voidakseen käyttää niitä. Heille on opetettu operaatioita ja toimintatapoja, mutta he eivät ole vielä taitavia niissä. Siksi ei voida sanoa, että he ”tuntevat” heidät.

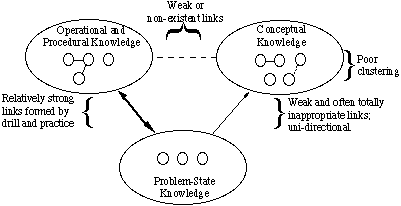Kuva. 3: esitys noviisien tietorakenteesta

yhteydet käsitteiden ja EOPs: n välillä ovat heikkoja tai olemattomia. Yhteys käsitteiden ja ongelmatilanteiden välillä on myös heikko. Näin noviisi ei voi analysoida ongelmaa eikä päättää tiettyjen yhtälöiden sopivuudesta. Ongelmatilanteiden ja EOPs: n väliset yhteydet ovat suhteellisen vahvoja, mutta linkit perustuvat ensisijaisesti määriin, jotka yhtälöillä on yhteistä ongelman Givensin ja eksplisiittisten tuntemattomien kanssa.

teema 2: Millaisissa kognitiivisissa prosesseissa opiskelijoiden on sitouduttava kehittämään sopivia tietorakenteita?

vastataksemme tähän kysymykseen meidän on ensin ymmärrettävä, miten asiantuntijat ja aloittelijat ratkaisevat ongelmia eri tavalla.

aloittelijat ovat yleensä epäonnistuneita yrittäessään ratkaista fysiikan tyypillisiä ongelmia. Käyttämällä mallia edustamaan prosessia, miten tyypillinen noviisi ratkaisee ongelman? Koska noviisin tietorakenteen vahvimmat yhteydet ovat ongelmatilanteiden ja yhtälöiden välillä, ongelman lukeminen ehdottaa välittömästi yhtälöitä, joihin liittyy ongelmassa nimenomaisesti annettuja määriä (tunnettuja ja tuntemattomia). Määrittämättä sovellettavuutta näiden yhtälöiden, ja yrittämättä ajatella muita yhtälöitä, jotka saattavat liittyä samat määrät, noviisi yleensä alkaa manipuloida tutuin yhtälöt, kunnes tuntematon voidaan ratkaista. Viimeisin luokassa käsitelty yhtälö on helpoimmin lähestyttävä ja nopeimmin mieleen palautettava. Niinpä noviisi etsii ja (jos” onnistuu”) löytää vain yhden tavan ratkaista ongelma ja yleensä pysähtyy, tutkimatta muita mahdollisuuksia ja analysoimatta ongelmatilannetta. Näin löydetyt yhtälöt ovat usein epätarkoituksenmukaisia, koska noviisit eivät usein käytä käsitteitä perustellakseen niiden soveltamista. Vaikka opiskelijat ajautuisivat käyttämään käsitteitä analysoimalla ongelmia etukäteen, heidän yhteytensä EOPs: aan ovat yleensä liian heikkoja ollakseen hyödyllisiä ongelmanratkaisussa. Myös käsitteiden ja ongelmatilanteiden väliset yhteydet ovat yksisuuntaisia, joten analogiat eivät ole erityisen hyödyllisiä: Noviisit eivät voi käyttää analogioita ongelmien ratkaisemiseen, koska he eivät voi tunnistaa, mitkä heidän jo ratkaisemistaan ongelmista ovat käsitteellisesti samanlaisia kuin ne, joita he parhaillaan yrittävät ratkaista. Sen sijaan aloittelijat käyttävät pintaominaisuuksia määrittääkseen ”samankaltaisuuden” ja yrittävät ratkaista uusia ongelmia, jotka perustuvat niiden samankaltaisuuteen jo ratkaisemiensa ongelmien pintaominaisuuksien kanssa.

koska asiantuntijat luokittelevat ongelmat ja EOPs: n samojen kattokäsitteiden mukaan, he voivat usein siirtyä suoraan ongelmatilanteista sopiviin yhtälöihin, operaatioihin ja/tai menetelmiin. Koska eri kategorioiden väliset yhteydet ovat vahvoja, vaikeat ongelmat (joiden osalta suoraa yhteyttä ongelmatilojen ja EOPs: n välillä ei vielä ole) voidaan ratkaista tietoisesti vetoamalla käsitteisiin, jolloin ongelmatilat voidaan epäsuorasti yhdistää asianmukaisiin EOP: iin(EOP). Koska käsitteiden ja ongelmatilanteiden väliset yhteydet ovat kaksisuuntaisia, analogiat ovat asiantuntijoille erittäin hyödyllinen ongelmanratkaisuväline. Lopuksi asiantuntijoilla on yleensä useampi kuin yksi tapa ratkaista jokin tietty ongelma.

tässä on yhteenveto suurimmista eroista asiantuntijoiden ja aloittelevien välillä:

1. aloittelevilla on huono käsitteiden ryhmittymä, mikä johtaa usein väärinkäsityksiin. Asiantuntijoilla on runsaasti käsitteitä, ongelmatilanteita, yhtälöitä, menettelyjä ja toimintoja, mikä johtaa parempaan ongelmanratkaisukykyyn.
2. aloittelevilla on yleensä vain yksi tapa ratkaista tietty ongelma, kun taas asiantuntijat voivat usein löytää useamman kuin yhden tavan. Siksi asiantuntija voi yrittää ratkaista epäjohdonmukaisuuksia niiden ilmetessä ja tarkistaa vastauksia, kun taas aloittelijat eivät tiedä epäjohdonmukaisuuksista eivätkä voi tarkistaa vastauksiaan.
3. aloittelijat käyttävät usein yhtälön manipulointia ja harvoin konseptipohjaisia strategioita saadakseen vastauksen. Asiantuntija käyttää käsitteitä ja analogioita ehdottaakseen useita ratkaisumenetelmiä ja suunnittelee strategian oikean vastauksen löytämiseksi.
4. aloittelijat eivät usein saa oikeaa vastausta, ja kun he saavat oikean vastauksen, se voi helposti olla väärästä syystä. Kun noviisi saa oikean vastauksen väärästä syystä, väärinkäsitykset vahvistuvat ja tulevat entistä vaikeammiksi voittaa. Asiantuntija saa yleensä oikean vastauksen ja osaa selittää, miksi vastaus on oikea.

on olemassa erilaisia kognitiivisia prosesseja, jotka auttavat aloittelijoita kehittämään konseptipohjaisen ongelmanratkaisumallin, jonka jaamme kolmeen kategoriaan: Analyysiprosessit, Päättelyprosessit ja Metakognitiiviset prosessit.

Analyysiprosessit

• ongelma-analyysi, kuten ongelmaesityksen rakentaminen.
• Käsiteanalyysi, kuten käsitteiden käyttäminen fysikaalisten objektien kvalitatiivisen käyttäytymisen määrittämiseen tai strategian muodostamiseen.
• strateginen analyysi, kuten ongelmatilanteen kannalta merkityksellisten fysiikan periaatteiden tunnistaminen ja oikeuttaminen.
• Representatiivinen analyysi, kuten ongelman eri representaatioiden tutkiminen.
• kompleksinen konstruktiivinen analyysi, kuten kompleksisen tilanteen hajottaminen yksinkertaisemmiksi.

Päättelyprosessit

• vertaaminen ja vastakkaisuus, kuten sen selvittäminen, miten asiat, tilanteet tai olosuhteet ovat samanlaisia ja/tai erilaisia.
• tulkitsemassa esimerkiksi asemakaavan muotoa vs. aika arvioida kohteen kiihtyvyys.
• erikoistapauksia ja rajoittavia tapauksia, eli äärimmäisten ja/tai tunnettujen tilojen tutkimista.
• prototyyppi – ja vastaesimerkit, esimerkiksi arkkityyppisten kategorioiden synnyttäminen.
• yleistys eli jonkin olosuhteen tai tilanteen keskeisten piirteiden tunnistaminen.

Metakognitiiviset prosessit

• pohdinta, eli itseohjautuva katselmus tarkoituksesta, tavoitteista, kokemuksen vaikutuksista jne.
• Meta-viestintä, joka on tietoista osallistumista kommunikaatiolinjojen muodostamiseen ja hiomiseen opettajan ja muiden oppilaiden kanssa sekä oppimisen tavoitteista päättämiseen.
• itsearviointi, kuten oman suorituksen arviointi tai ongelmien ratkaisemisen vaikeuksien syiden tunnistaminen.

näihin ja muihin prosesseihin kannustetaan opetussuunnitelmamateriaaleillamme. Seuraavassa jaksossa esitellään tähän tarvittavat erityistoimenpiteet.

teema 3: Millaiset oppimistoimet tai-kokemukset edistävät näitä hyödyllisiä kognitiivisia prosesseja?

opettajat voivat käyttää seuraavia toimintoja stimuloimaan kognitiivisia prosesseja, joita tarvitaan fysiikan käsitteellisen ymmärtämisen kehittämiseen:

1. Käytä useita esityksiä. Esitys voi olla kielellinen, Abstrakti, symbolinen, kuvallinen tai konkreettinen. Käyttämällä useita eri representaatioita samaan tietoon, ja ottaa opiskelijat kääntää välillä representaatioita, auttaa opiskelijaa inter-relate tietotyypit ja suhteuttaa tietoa fyysiseen kokemukseen. Se edistää tiedon elementtien välisten yhteyksien muodostumista ja tiedon runsasta ryhmittelyä.
2. tee eteen-ja taaksepäin viittauksia. Käsitteiden muodostaminen vaatii pitkän ajan. Näin et voi odottaa, että opiskelijat oppivat kokonaan yhden aiheen ennen siirtymistä seuraavaan. Tekemällä eteenpäin viittauksia, valmistat opiskelija uutta materiaalia. Takautuvilla viittauksilla yhdistetään Uusi aineisto vakiintuneeseen (tai osittain vakiintuneeseen) materiaaliin, jolloin tieto nivoutuu ja kytkeytyy toisiinsa lineaarisen sijaan.
3. tutki laajennettuja Konteksteja. Käsitteet voivat olla erittäin kontekstiriippuvaisia, eivätkä ne tule globaalisti käyttökelpoisiksi ennen kuin ne on abstrahoitu. Laajan sovellettavuuskontekstin tutkiminen auttaa oppilasta tarkentamaan ja abstrahoimaan käsitteitä. Se myös välttää virheellisiä tai liian yksinkertaistettuja yleistyksiä.
4. vertaa ja vertaa. Olennaista tiedon jäsentämisessä (tai uudelleen jäsentämisessä) on tiedon elementtien luokittelu ja keskinäinen suhde. Vertailut ja kontrastit herkistävät opiskelijat luokkiin ja suhteisiin ja auttavat oppilaita hahmottamaan yhtäläisyyksiä ja eroja, joita tarvitaan heidän tietovarastonsa järjestämiseen.
5. luokittele ja luokittele. Vertailujen ja vastakohtien rinnalla opiskelijan tulee olla tietoinen luokista ja luokittelujärjestelmistä. Opiskelijoiden on myös harjoiteltava luokittelujärjestelmien luomista ja tunnistamista. Vaatimalla opiskelijoita luokittelemaan kohteita, valitsemaan nimiä luokilleen ja selittämään järjestelmäänsä, voimme auttaa opiskelijoita uudelleen jäsentämään tietovarastonsa.
6. ennusta & Näytä (vanhan mallin riittämättömyys). Huolellisesti valikoiduilla demonstraatioilla ja kokeiluilla voidaan tuoda esiin opiskelijamallien epäjohdonmukaisuuksia. Opiskelijoille pitäisi näyttää set-up tai kokeellinen laite ja olisi pyydettävä ennustamaan, mitä tapahtuu, kun jotain tehdään. On tärkeää, että opiskelijat tekevät ennusteita etukäteen, jolloin he ovat tietoisia omasta mallistaan. Opiskelijat harkitsevat vaihtoehtoisia käsityksiä vain, jos oma epäonnistuu. Oppilaiden vaatiminen käyttämään mallejaan ja sen osoittaminen, miten heidän mallinsa ovat epäjohdonmukaisia tai riittämättömiä, valmistaa heitä luomaan parempia (vaikkakin omia) malleja.

7. selitä(tiivistää, kuvata, keskustella, määritellä jne.). Vakio-ongelmat harvoin kertovat opettajalle sitä, mitä oppilaat eivät ymmärrä. Vaikka opiskelijat saavat ongelman oikein, voi silti olla epäselvyyttä käytettyjen yhtälöiden sovellettavuudesta. Vaaditaan opiskelijoita selittämään, miten he ratkaisevat ongelman altistaa väärinkäsityksiä ja väärinkäsityksiä, ja auttaa opiskelijoita uudelleen niiden tietovaraston. Lisäksi opiskelijat harvoin näkevät tavallisissa mielenosoituksissa ja kokeissa sitä, mitä asiantuntijat näkevät. Oppilaiden tulee selittää ja keskustella siitä, mitä he luulevat nähneensä (esimerkiksi ennustuksen aikana & Näytä), jotta opettaja voi olla vuorovaikutuksessa oppilaiden mallien kanssa. Lisäksi prosessi selittää (tai tiivistää, kuvailla, keskustella, jne.) auttaa opiskelijoita tuntemaan omat mallinsa sekä muiden opiskelijoiden mallit.

8. Luo useita ratkaisuja. Tehokasta ongelmanratkaisua ei voi tapahtua, elleivät opiskelijat valitse joukosta kelvollisia ratkaisupolkuja. Ratkaisemalla ongelmia useammalla kuin yhdellä tavalla opiskelijat oppivat priorisoimaan strategisen osaamisensa elementtejä.

9. Suunnittele, perustele ja strategisoi. Hyvin harvat suhteet fysiikassa ovat aina päteviä. Yhtälön manipuloinnin välttämiseksi oppilaita tulisi pyytää suunnittelemaan (ja sitten selittämään), miten he ratkaisevat ongelmia. Opiskelijoiden on opittava, miten määrittää, mitkä käsitteet ovat merkityksellisiä (ja mitkä ovat merkityksettömiä) mihinkään tiettyyn ongelmatilanteeseen ja miten toteuttaa asiaankuuluvat käsitteet ongelman ratkaisemiseksi. Ottaa opiskelijat luoda omia strategioita auttaa heitä oppimaan, miten käsitteitä käytetään ratkaisemaan ongelmia.
10. heijastavat (arvioivat, integroivat, laajentavat, yleistävät jne.) Suoritettuaan useimmat toiminnot, opiskelijat hyötyvät katsoa taaksepäin, mitä he ovat tehneet. Millaisia kuvioita he ovat havainneet? Mitä yleisiä sääntöjä voidaan laatia? Muunlainen toiminta antaa opiskelijoille tarvittavat palaset yhtenäisen kuvan luomiseksi fysiikasta, mutta jonkinlainen heijastava toiminta on yleensä tarpeen ”koota palaset yhteen”.
11. Meta-kommunikoi oppimisprosessista. Oppia fysiikan (tai jokin muu monimutkainen aihe), opiskelijoiden on tullut itse investoinut. Heidän on altistuttava muiden ihmisten (opettajan ja oppilaan) malleille. Heitä on varoitettava siitä, että viestinnän täsmällisyys on välttämätöntä, heille on tiedotettava yhteisistä sudenkuopista ja vääristä tulkinnoista ja heille on kerrottava, että heidän on jäsenneltävä tietonsa uudelleen. Oppilaiden on opittava, miten he oppivat parhaiten.