Les bases: KNN pour la classification et la régression

Science des données à partir de zéro

Les cours de science des données ou de statistiques appliquées commencent généralement par des modèles linéaires, mais à sa manière, les K-voisins les plus proches sont probablement le modèle le plus simple et largement utilisé conceptuellement. Les modèles KNN ne sont en réalité que des implémentations techniques d’une intuition commune, selon laquelle les choses qui partagent des caractéristiques similaires ont tendance à être, enfin, similaires. Ce n’est guère un aperçu approfondi, mais ces implémentations pratiques peuvent être extrêmement puissantes et, surtout pour quelqu’un qui s’approche d’un ensemble de données inconnu, peuvent gérer des non-linéarités sans aucune ingénierie de données ou configuration de modèle compliquée.

Quoi

À titre d’exemple illustratif, considérons le cas le plus simple d’utilisation d’un modèle KNN comme classificateur. Supposons que vous ayez des points de données qui appartiennent à l’une des trois classes. Un exemple en deux dimensions peut ressembler à ceci:

Vous pouvez probablement voir assez clairement que les différentes classes sont regroupées — le coin supérieur gauche des graphiques semble appartenir à la classe orange, la section droite / centrale à la classe bleue. Si on vous donnait les coordonnées du nouveau point quelque part sur le graphique et qu’on vous demandait à quelle classe il était susceptible d’appartenir, la plupart du temps, la réponse serait assez claire. Tout point dans le coin supérieur gauche du graphique est susceptible d’être orange, etc.

La tâche devient cependant un peu moins certaine entre les classes, où nous devons nous contenter d’une limite de décision. Considérez le nouveau point ajouté en rouge ci-dessous:

Ce nouveau point doit-il être classé comme orange ou bleu? Le point semble se situer entre les deux groupes. Votre première intuition pourrait être de choisir le cluster le plus proche du nouveau point. Ce serait l’approche du « plus proche voisin », et bien qu’elle soit conceptuellement simple, elle donne souvent des prédictions assez sensées. À quel point précédemment identifié le nouveau point est-il le plus proche ? Il n’est peut-être pas évident de simplement regarder le graphique quelle est la réponse, mais il est facile pour l’ordinateur de parcourir les points et de nous donner une réponse:

, il semble que le point le plus proche soit dans la catégorie bleue, donc notre nouveau point l’est probablement aussi. C’est la méthode du voisin le plus proche.

À ce stade, vous vous demandez peut-être à quoi sert le « k » dans les k-plus proches voisins. K est le nombre de points voisins que le modèle examinera lors de l’évaluation d’un nouveau point. Dans notre exemple le plus proche voisin le plus simple, cette valeur pour k était simplement 1 — nous avons regardé le voisin le plus proche et c’était tout. Vous auriez pu, cependant, choisir de regarder les 2 ou 3 points les plus proches. Pourquoi est-ce important et pourquoi quelqu’un définirait-il k à un nombre plus élevé? D’une part, les frontières entre les classes peuvent se heurter les unes aux autres de manière à rendre moins évident que le point le plus proche nous donnera la bonne classification. Considérons les régions bleues et vertes dans notre exemple. En fait, zoomons sur eux:

Remarquez que si les régions globales semblent suffisamment distinctes, leurs limites semblent être un peu entrelacées les unes avec les autres. C’est une caractéristique commune des ensembles de données avec un peu de bruit. Lorsque c’est le cas, il devient plus difficile de classer les choses dans les zones limites. Considérez ce nouveau point:

D’une part, visuellement, il semble que le point précédemment identifié le plus proche soit bleu, ce que notre ordinateur peut facilement confirmer pour nous:

D’autre part, ce point bleu le plus proche semble être un peu une valeur aberrante elle-même, loin du centre de la région bleue et en quelque sorte entouré de points verts. Et ce nouveau point est même à l’extérieur de ce point bleu! Et si nous regardions les trois points les plus proches du nouveau point rouge?

Ou même les cinq points les plus proches du nouveau point?

Maintenant, il semble que notre nouveau point soit dans un quartier vert! Il se trouve qu’il y a un point bleu à proximité, mais la prépondérance ou les points à proximité sont verts. Dans ce cas, il serait peut-être logique de définir une valeur plus élevée pour k, de regarder une poignée de points voisins et de les faire voter d’une manière ou d’une autre sur la prédiction du nouveau point.

Le problème illustré est trop approprié. Lorsque k est défini sur un, la frontière entre les régions identifiées par l’algorithme comme étant bleues et vertes est cahoteuse, elle serpente avec chaque point individuel. Le point rouge semble être dans la région bleue:

Amenant k à 5, cependant, lisse la limite de décision lorsque les différents points voisins votent. Le point rouge semble maintenant fermement dans le quartier vert:

Le compromis avec des valeurs plus élevées de k est la perte de granularité dans la limite de décision. Définir k très haut aura tendance à vous donner des limites lisses, mais les limites du monde réel que vous essayez de modéliser peuvent ne pas être parfaitement lisses.

En pratique, nous pouvons utiliser le même type d’approche des voisins les plus proches pour les régressions, où nous voulons une valeur individuelle plutôt qu’une classification. Considérez la régression suivante ci-dessous:

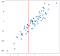
Les données ont été générées de manière aléatoire, mais ont été générées de manière linéaire, de sorte qu’un modèle de régression linéaire conviendrait naturellement bien à ces données. Je tiens à souligner, cependant, que vous pouvez approximer les résultats de la méthode linéaire d’une manière conceptuellement plus simple avec une approche K-voisins les plus proches. Notre « régression » dans ce cas ne sera pas une formule unique comme un modèle OLS nous le donnerait, mais plutôt une meilleure valeur de sortie prévue pour une entrée donnée. Considérez la valeur de -.75 sur l’axe des abscisses, que j’ai marqué d’une ligne verticale:

Sans résoudre d’équations, nous pouvons arriver à une approximation raisonnable de ce que devrait être la sortie simplement en considérant les points voisins:

Il est logique que la valeur prévue soit proche de ces points, pas beaucoup plus basse ou plus élevée. Peut-être qu’une bonne prédiction serait la moyenne de ces points:

Vous pouvez imaginer le faire pour toutes les valeurs d’entrée possibles et proposer des prédictions partout:

Connecter toutes ces prédictions avec une ligne nous donne notre régression:

Dans ce cas, les résultats ne sont pas une ligne claire, mais ils tracent raisonnablement bien la pente ascendante des données. Cela peut ne pas sembler terriblement impressionnant, mais l’un des avantages de la simplicité de cette implémentation est qu’elle gère bien la non-linéarité. Considérez cette nouvelle collection de points:

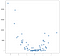
Ces points ont été générés en mettant simplement au carré les valeurs de l’exemple précédent, mais supposons que vous soyez tombé sur un ensemble de données comme celui-ci dans la nature. Ce n’est évidemment pas de nature linéaire et bien qu’un modèle de style OLS puisse facilement gérer ce type de données, il nécessite l’utilisation de termes non linéaires ou d’interaction, ce qui signifie que le data scientist doit prendre des décisions sur le type d’ingénierie des données à effectuer. L’approche KNN ne nécessite aucune autre décision — le même code que j’ai utilisé sur l’exemple linéaire peut être réutilisé entièrement sur les nouvelles données pour produire un ensemble de prédictions réalisables:

Comme pour les exemples de classificateurs, la définition d’une valeur supérieure k nous aide à éviter un surajustement, même si vous risquez de perdre du pouvoir prédictif à la marge, en particulier sur les bords de votre ensemble de données. Considérons le premier exemple d’ensemble de données avec des prédictions faites avec k défini sur un, c’est-à-dire une approche du voisin le plus proche:

Nos prédictions sautent de manière erratique lorsque le modèle passe d’un point de l’ensemble de données à l’autre. En revanche, la définition de k à dix, de sorte que dix points totaux soient moyennés ensemble pour la prédiction, donne un trajet beaucoup plus fluide:

En général, cela semble mieux, mais vous pouvez voir quelque chose d’un problème aux bords des données. Parce que notre modèle prend en compte autant de points pour une prédiction donnée, lorsque nous nous rapprochons de l’un des bords de notre échantillon, nos prédictions commencent à s’aggraver. Nous pouvons résoudre ce problème quelque peu en pondérant nos prédictions aux points les plus proches, bien que cela comporte ses propres compromis.

Comment

Lors de la configuration d’un modèle KNN, seule une poignée de paramètres doivent être choisis / peuvent être modifiés pour améliorer les performances.

K : le nombre de voisins: Comme discuté, l’augmentation de K aura tendance à lisser les limites de décision, évitant un surajustement au prix d’une certaine résolution. Il n’y a pas de valeur unique de k qui fonctionnera pour chaque ensemble de données. Pour les modèles de classification, en particulier s’il n’y a que deux classes, un nombre impair est généralement choisi pour k. C’est ainsi que l’algorithme ne rencontre jamais une « égalité »: par exemple, il examine les quatre points les plus proches et constate que deux d’entre eux sont dans la catégorie bleue et deux sont dans la catégorie rouge.

Distance métrique: Il s’avère qu’il existe différentes façons de mesurer à quel point deux points sont « proches » l’un de l’autre, et les différences entre ces méthodes peuvent devenir significatives dans des dimensions plus élevées. Le plus couramment utilisé est la distance euclidienne, le tri standard que vous avez peut-être appris au collège en utilisant le théorème de Pythagore. Une autre mesure est ce qu’on appelle la « distance de Manhattan », qui mesure la distance prise dans chaque direction cardinale, plutôt que le long de la diagonale (comme si vous marchiez d’une intersection de rue à Manhattan à une autre et deviez suivre la grille de rues plutôt que de pouvoir prendre la route la plus courte « à vol d’oiseau »). Plus généralement, il s’agit en fait des deux formes de ce qu’on appelle la  » distance de Minkowski « , dont la formule est:

Lorsque p est défini sur 1, cette formule est la même que la distance de Manhattan, et lorsqu’elle est définie sur deux, la distance euclidienne.

Poids: Une façon de résoudre à la fois le problème d’une éventuelle « égalité » lorsque l’algorithme vote sur une classe et le problème où nos prédictions de régression se sont aggravées vers les bords de l’ensemble de données consiste à introduire une pondération. Avec des poids, les points proches compteront plus que les points plus éloignés. L’algorithme examinera toujours tous les k voisins les plus proches, mais les voisins les plus proches auront plus de voix que ceux qui sont plus éloignés. Ce n’est pas une solution parfaite et évoque la possibilité de surajuster à nouveau. Considérons notre exemple de régression, cette fois avec des poids:

Nos prédictions vont maintenant jusqu’au bord de l’ensemble de données, mais vous pouvez voir que nos prédictions se rapprochent maintenant beaucoup plus des points individuels. La méthode pondérée fonctionne raisonnablement bien lorsque vous êtes entre des points, mais à mesure que vous vous rapprochez de plus en plus d’un point particulier, la valeur de ce point a de plus en plus d’influence sur la prédiction de l’algorithme. Si vous vous approchez suffisamment d’un point, c’est presque comme si vous mettiez k à un, car ce point a tellement d’influence.

Mise à l’échelle / normalisation: Un dernier point, mais d’une importance cruciale, est que les modèles KNN peuvent être rejetés si différentes variables d’entités ont des échelles très différentes. Considérons un modèle qui tente de prédire, par exemple, le prix de vente d’une maison sur le marché en fonction de caractéristiques telles que le nombre de chambres et la superficie totale de la maison, etc. Il y a plus de variance dans le nombre de pieds carrés dans une maison que dans le nombre de chambres à coucher. En règle générale, les maisons n’ont qu’une petite poignée de chambres, et même le plus grand manoir n’aura pas des dizaines ou des centaines de chambres. Les pieds carrés, en revanche, sont relativement petits, de sorte que les maisons peuvent aller de près de, disons, 1 000 pieds carrés du petit côté à des dizaines de milliers de pieds carrés du grand côté.

Considérez la comparaison entre une maison de 2 000 pieds carrés avec 2 chambres et une maison de 2 010 pieds carrés avec deux chambres — 10 pieds carrés. les pieds ne font guère de différence. En revanche, une maison de 2 000 pieds carrés avec trois chambres à coucher est très différente et représente une disposition très différente et peut-être plus exiguë. Un ordinateur naïf n’aurait cependant pas le contexte pour comprendre cela. On dirait que la chambre 3 n’est qu’à « une » unité de la chambre 2, tandis que le pied de page de 2 010 pieds carrés est à « dix » du pied de page de 2 000 pieds carrés. Pour éviter cela, les données d’entités doivent être mises à l’échelle avant d’implémenter un modèle KNN.

Forces et faiblesses

Les modèles KNN sont faciles à mettre en œuvre et à bien gérer les non-linéarités. L’ajustement du modèle a également tendance à être rapide: l’ordinateur n’a pas à calculer de paramètres ou de valeurs particuliers, après tout. Le compromis ici est que si le modèle est rapide à mettre en place, il est plus lent à prédire, car pour prédire un résultat pour une nouvelle valeur, il devra parcourir tous les points de son ensemble d’entraînement pour trouver les plus proches. Pour les grands ensembles de données, KNN peut donc être une méthode relativement lente par rapport à d’autres régressions qui peuvent prendre plus de temps à s’adapter, mais qui font ensuite leurs prédictions avec des calculs relativement simples.

Un autre problème avec un modèle KNN est qu’il manque d’interprétabilité. Une régression linéaire OLS aura des coefficients clairement interprétables qui peuvent eux-mêmes donner une indication de la « taille de l’effet » d’une caractéristique donnée (bien qu’il faille faire preuve de prudence lors de l’attribution de la causalité). Cependant, demander quelles fonctionnalités ont le plus grand effet n’a pas vraiment de sens pour un modèle KNN. En partie à cause de cela, les modèles KNN ne peuvent pas non plus être vraiment utilisés pour la sélection de fonctionnalités, de la même manière qu’une régression linéaire avec un terme de fonction de coût supplémentaire, comme ridge ou lasso, ou la façon dont un arbre de décision choisit implicitement les fonctionnalités qui semblent les plus précieuses.