L’énergie cinétique est l’énergie du mouvement. Une expression de l’énergie cinétique est dérivée en regardant le cas d’un objet qui est soulevé à une certaine hauteur relative (ainsi, le travail est effectué sur cet objet) et ensuite laissé tomber.
Termes clés
o Énergie cinétique
Objectifs
o Dériver une expression de l’énergie cinétique du concept physique du travail
o Comprendre la relation entre travail et énergie cinétique
o Calculer l’énergie cinétique de divers objets
Commençons!
Relier le Travail et l’Énergie cinétique
Dans un certain sens, le travail est la quantité d’énergie mise dans une tâche (ou, peut-être, « mise dans l’objet »). Par exemple, imaginez que nous ramassions un objet du sol et l’élevions à une certaine hauteur; nous avons fait un certain travail sur cet objet. Cependant, si nous le laissons aller, cela s’accélère, comme si le travail que nous avons fait pour soulever l’objet était en train de se transformer en mouvement. Grâce à cet exemple, nous pouvons dériver une définition de l’énergie cinétique, qui est l’énergie du mouvement. Cette définition, comme nous le verrons, est étroitement liée à la façon dont nous avons défini le travail.
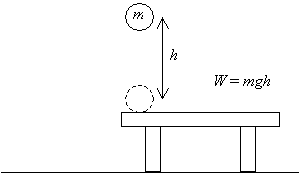
Tout d’abord, considérons un objet: une boule de masse m. Nous allons ramasser la balle sur une table et l’élever à une distance h au-dessus de cette table, comme indiqué ci-dessous. Nous avons donc fait une quantité de travail W = mgh, (ce résultat est le produit de l’amplitude du vecteur déplacement (h) et de la force appliquée (mg)the les vecteurs correspondants sont parallèles).
Maintenant, si nous relâchons cette balle et la laissons tomber de la hauteur h au-dessus de la table, une fois qu’elle reviendra à sa hauteur d’origine (le niveau de la table), elle aura une certaine vitesse v résultant de l’accélération due à la gravité.
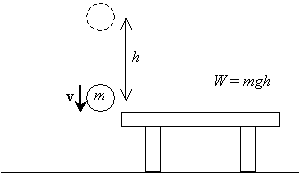
Nous voulons calculer cette vitesse (ou vitesse, techniquementwe nous pouvons parfois remplacer le terme vitesse par vitesse, mais sachez toujours que la vitesse est en fait un vecteur et que la vitesse est l’amplitude de la vitesse). Nous savons que l’accélération due à la gravité est constante et que la vitesse initiale de la balle est nulle (elle est stationnaire avant d’être relâchée). Nous supposerons que la hauteur initiale de la balle est h et que sa hauteur finale est nulle (le niveau de la table). Pour calculer la vitesse en dérivant les formules appropriées, nous avons besoin de l’utilisation du calcul intégral élémentaire. (Si vous êtes un étudiant avancé ou cherchez un défi supplémentaire, vous pouvez essayer de dériver ces formules dans les conditions ci-dessus vous-même. Il suffit de noter que la vitesse v de la balle est la vitesse temporelle de changement de sa position x en fonction du temps t, ![]() , et que l’accélération a est la vitesse temporelle de changement de la vitesse,
, et que l’accélération a est la vitesse temporelle de changement de la vitesse, ![]() .)
.)
![]()
![]()
Ces formules expriment la vitesse en fonction du temps, v(t), et la position (hauteur) en fonction du temps, x(t), en termes d’accélération a, de hauteur h et de temps t. Nous savons que a =–g, puisque la balle n’est accélérée que par la gravité et que cette accélération est vers le bas (d’où le signe négatif). La position finale de la balle est de zéro mètre, ou x(t) = 0. Calculons t, le temps écoulé entre la libération de la balle et son arrivée au niveau de la table.
![]()
![]()
![]()
Maintenant, calculons la vitesse de la balle à ce moment.
![]()
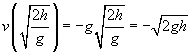
Comparons maintenant ce résultat avec le travail effectué à l’origine sur l’objet: W = mgh. Notez à quel point ces deux expressions sont proches dans la forme; en fait, le seul facteur manquant à la vitesse est la masse de la balle, m. Si nous avons carré la vitesse, multipliée par m, puis divisée par 2, nous aurions en fait la même expression que l’œuvre!
![]()
Ainsi, nous pouvons voir dans un certain sens comment la définition de l’énergie cinétique peut être dérivée. L’énergie cinétique K d’un objet est donc un scalaire défini comme suit, où m est la masse de l’objet et v sa vitesse:
![]()
Il s’avère que l’énergie cinétique est le travail effectué sur un objet par la force nette sur cet objet. Ainsi, bien qu’une femme puisse effectuer un certain travail sur un objet en le soulevant d’une hauteur à une autre, la force nette sur cet objet est nulle (la femme applique une force égale à mais opposée dans le sens de la gravité). Ainsi, il n’y a pas de changement d’énergie cinétique. Si cet objet est libéré et laissé tomber, cependant, il gagne de l’énergie cinétique car la force nette sur lui est simplement celle de la gravité (une seule force). Ainsi, pour comprendre la relation entre l’énergie cinétique et le travail, nous devons affiner quelque peu notre concept de travail. Si nous définissons le travail W comme le travail total effectué sur l’objet par toutes les forces (en d’autres termes, le travail effectué sur l’objet par la force nette), alors la relation suivante entre le travail W et les énergies cinétiques initiale et finale (Ki et Kf) tient.
![]() où
où ![]()
Ainsi, le travail net effectué sur un objet est égal à la variation de l’énergie cinétique de cet objet (ΔK). Les problèmes de pratique suivants vous donnent l’occasion de tester et d’appliquer votre compréhension des concepts de travail et d’énergie cinétique.
Problème de pratique: Un projectile de masse 1 kilogramme se déplace à 5 mètres par seconde. À quelle vitesse un projectile de 0,1 kilogramme doit-il se déplacer pour obtenir la même énergie cinétique?
Solution: D’abord, calculons l’énergie cinétique du projectile le plus massif (1 kilogramme).
![]()
Nous pouvons maintenant calculer la vitesse de l’objet le moins massif de telle sorte qu’il possède cette même énergie cinétique, K.
![]()
![]()
![]()
Problème de pratique: Un homme soulève un poids de 15 kilogrammes à une hauteur de deux mètres du sol avant de le laisser tomber. Dans l’instant avant que le poids n’entre en contact avec le sol, quelle est sa vitesse?
Solution: Dessinons un diagramme illustrant les forces agissant sur l’objet lorsqu’il est soulevé et lorsqu’il tombe; ces forces incluent la gravité (Fg) et la force ascendante que l’homme applique (Fu).
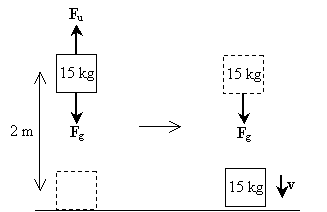
Notez que la première étape du processus (soulever le poids) n’implique aucune force nette agissant sur l’objet– la force due à la gravité est équilibrée par la force que l’homme applique pour soulever le poids. Dans la deuxième étape, cependant, le poids n’éprouve que la force de gravité. La force nette, dans ce cas, est donc mg dans le sens descendant. En tant que tel, la vitesse de l’objet est également dans la direction descendante. Le travail effectué sur le poids à la suite de la gravité est simplement mgh; c’est aussi le travail total effectué sur le poids tout au long du processus. Notez que l’énergie cinétique initiale du poids est nulle car sa vitesse est nulle. Calculons maintenant la vitesse en appliquant la relation entre le travail net et le changement d’énergie cinétique.