La stationnarité signifie que les propriétés statistiques d’une série chronologique, c’est-à-dire la moyenne, la variance et la covariance, ne changent pas avec le temps. De nombreux modèles statistiques exigent que la série soit stationnaire pour faire des prédictions efficaces et précises.
Deux tests statistiques seraient utilisés pour vérifier la stationnarité d’une série temporelle – Test de Dickey Fuller augmenté (« ADF ») et test de Kwiatkowski-Phillips-Schmidt-Shin (« KPSS »). Une méthode pour convertir une série chronologique non stationnaire en série stationnaire doit également être utilisée.
Cette première cellule importe des packages standard et définit les tracés pour qu’ils apparaissent en ligne.
:
%matplotlib inlineimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport statsmodels.api as sm
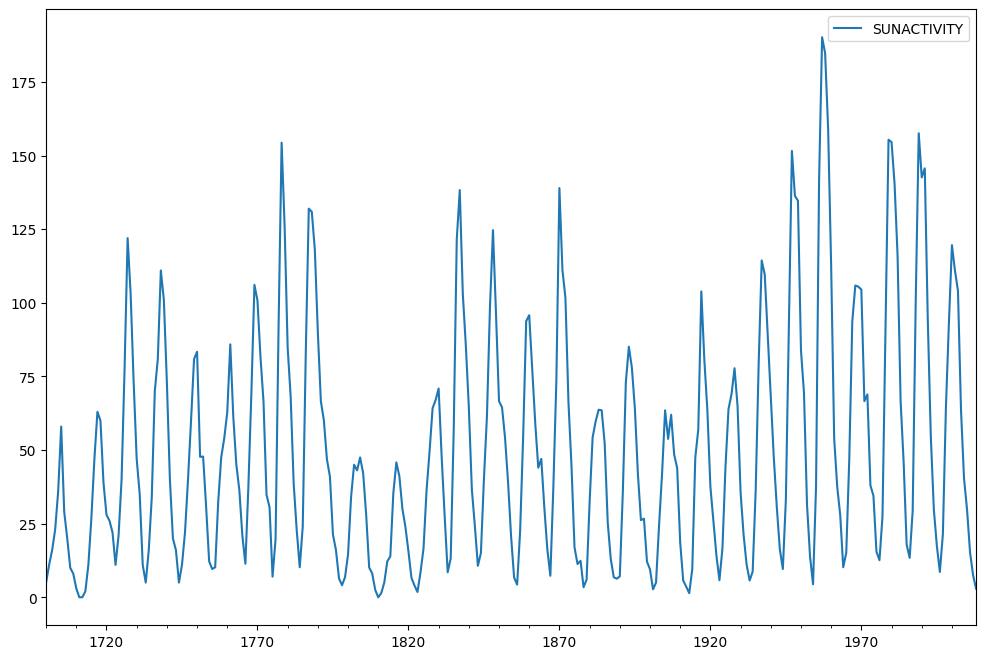
Le jeu de données Sunspots est utilisé. Il contient des données annuelles (1700-2008) sur les taches solaires provenant du Centre national de données géophysiques.
:
sunspots = sm.datasets.sunspots.load_pandas().data
Un certain prétraitement est effectué sur les données. La colonne « ANNÉE » est utilisée pour créer un index.
:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))del sunspots
Les données sont tracées maintenant.
:
sunspots.plot(figsize=(12,8))
:
<AxesSubplot:>
Test ADF¶
Le test ADF est utilisé pour déterminer la présence d’une racine unitaire dans la série, et aide donc à comprendre si la série est stationnaire ou non. Les hypothèses nulles et alternatives de ce test sont:
Hypothèse nulle: La série a une racine unitaire.
Hypothèse alternative: La série n’a pas de racine unitaire.
Si l’hypothèse nulle n’a pas été rejetée, ce test peut fournir la preuve que la série n’est pas stationnaire.
Une fonction est créée pour effectuer le test ADF sur une série chronologique.
:
from statsmodels.tsa.stattools import adfullerdef adf_test(timeseries): print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC') dfoutput = pd.Series(dftest, index=) for key,value in dftest.items(): dfoutput = value print (dfoutput)
Test KPSS¶
KPSS est un autre test pour vérifier la stationnarité d’une série chronologique. L’hypothèse nulle et alternative pour le test KPSS est opposée à celle du test ADF.
Hypothèse nulle : Le processus est stationnaire.
Hypothèse alternative: La série a une racine unitaire (la série n’est pas stationnaire).
Une fonction est créée pour effectuer le test KPSS sur une série temporelle.
:
from statsmodels.tsa.stattools import kpssdef kpss_test(timeseries): print ('Results of KPSS Test:') kpsstest = kpss(timeseries, regression='c', nlags="auto") kpss_output = pd.Series(kpsstest, index=) for key,value in kpsstest.items(): kpss_output = value print (kpss_output)
Les tests ADF donnent les résultats suivants : statistique de test, valeur p et valeur critique à des intervalles de confiance de 1%, 5% et 10%.
Le test ADF est maintenant appliqué aux données.
:
adf_test(sunspots)
Results of Dickey-Fuller Test:Test Statistic -2.837781p-value 0.053076#Lags Used 8.000000Number of Observations Used 300.000000Critical Value (1%) -3.452337Critical Value (5%) -2.871223Critical Value (10%) -2.571929dtype: float64
Sur la base du niveau de signification de 0,05 et de la valeur p du test ADF, l’hypothèse nulle ne peut être rejetée. Par conséquent, la série est non stationnaire.
Les tests KPSS donnent les résultats suivants : statistique de test, valeur p et valeur critique à des intervalles de confiance de 1%, 5% et 10%.
Le test KPSS est maintenant appliqué aux données.
:
kpss_test(sunspots)
Results of KPSS Test:Test Statistic 0.669866p-value 0.016285Lags Used 7.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
Sur la base du niveau de signification de 0,05 et de la valeur p du test KPSS, il existe des preuves pour rejeter l’hypothèse nulle en faveur de l’alternative. Par conséquent, la série est non stationnaire selon le test KPSS.
Il est toujours préférable d’appliquer les deux tests, afin de s’assurer que la série est vraiment stationnaire. Les résultats possibles de l’application de ces tests stationnaires sont les suivants:
Ici, en raison de la différence dans les résultats du test ADF et du test KPSS, on peut déduire que la série est stationnaire de tendance et non stationnaire stricte. La série peut être dégradée par différenciation ou par ajustement du modèle.
Réduction par différence¶
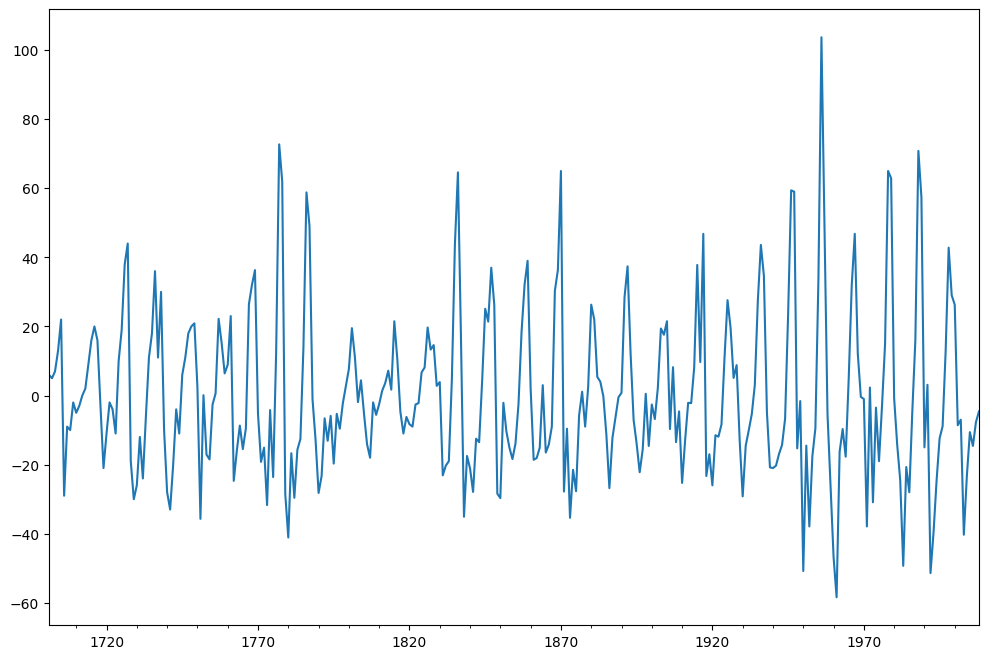
C’est l’une des méthodes les plus simples pour réduire une série chronologique. Une nouvelle série est construite où la valeur au pas de temps actuel est calculée comme la différence entre l’observation d’origine et l’observation au pas de temps précédent.
La différence est appliquée sur les données et le résultat est tracé.
:
sunspots = sunspots - sunspots.shift(1)sunspots.dropna().plot(figsize=(12,8))
:
<AxesSubplot:>
Le test ADF est maintenant appliqué sur ces valeurs détendues et la stationnarité est vérifiée.
:
adf_test(sunspots.dropna())
Results of Dickey-Fuller Test:Test Statistic -1.486166e+01p-value 1.715552e-27#Lags Used 7.000000e+00Number of Observations Used 3.000000e+02Critical Value (1%) -3.452337e+00Critical Value (5%) -2.871223e+00Critical Value (10%) -2.571929e+00dtype: float64
Sur la base de la valeur p du test ADF, il existe des preuves pour rejeter l’hypothèse nulle en faveur de l’alternative. Par conséquent, la série est strictement stationnaire maintenant.
Le test KPSS est maintenant appliqué à ces valeurs détendues et la stationnarité est vérifiée.
:
kpss_test(sunspots.dropna())
Results of KPSS Test:Test Statistic 0.021193p-value 0.100000Lags Used 0.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/stattools.py:1911: InterpolationWarning: The test statistic is outside of the range of p-values available in thelook-up table. The actual p-value is greater than the p-value returned. warn_msg.format(direction="greater"), InterpolationWarning
Sur la base de la valeur p du test KPSS, l’hypothèse nulle ne peut pas être rejetée. Par conséquent, la série est stationnaire.
Conclusion¶
Deux tests pour vérifier la stationnarité d’une série chronologique sont utilisés, à savoir le test ADF et le test KPSS. Le détritrage est effectué en utilisant la différenciation. Les séries chronologiques stationnaires de tendance sont converties en séries chronologiques stationnaires strictes. Le modèle de prévision requis peut maintenant être appliqué sur des données de séries chronologiques stationnaires.