Structure des connaissances

Extrait d’un livret accompagnant un atelier destiné aux professeurs de sciences du secondaire.

par Robert J. Dufresne, William J. Leonard et William J. Gerace

Notre groupe à l’UMass a développé un modèle cognitif qui nous aide à représenter les différences dans la façon dont les experts et les novices stockent et utilisent les connaissances sur le contenu. Le modèle nous aide également à cibler des domaines spécifiques sur lesquels les novices doivent se concentrer afin de mieux résoudre les problèmes. Cependant, le modèle n’est qu’une représentation de la structure de la connaissance, et il évolue constamment. Ainsi, il ne faut pas le prendre trop littéralement. Son utilité vient de sa capacité à fournir une manifestation concrète, aussi imparfaite soit-elle, des façons de penser des experts et des novices. Le modèle nous aide à discuter:

1. le stockage de connaissances spécifiques à un domaine ;
2. comportement de résolution de problèmes de type expert et novice;
3. la structure hiérarchique du magasin de connaissances d’un expert;
4. idées fausses;
5. les effets des questions sans but et dirigées vers des objectifs; et
6. le processus de méta-communication.

Dans cet atelier — et dans notre approche de la physique en général — il y a 3 thèmes de base:

1. Des types particuliers de connaissances et de structures de connaissances sont nécessaires pour résoudre efficacement les problèmes. Une grande partie de ces connaissances est de nature conceptuelle, par opposition à opérationnelle ou procédurale, et de puissantes structures de connaissances impliquent nécessairement des éléments conceptuels. La présence d’éléments conceptuels dans les structures de connaissances est la clé d’une « compréhension plus profonde » de la physique.
2. Des types particuliers de processus cognitifs sont nécessaires à l’acquisition de connaissances conceptuelles et à la construction de structures de connaissances utiles.
3. Il est possible de concevoir des activités qui favorisent ces processus cognitifs souhaitables. Dans de nombreux cas, ces activités ne sont que des actualisations des processus cognitifs eux-mêmes. (Ce point deviendra, espérons-le, plus clair plus tard.)

Nous développerons chacun de ces thèmes avant de nous concentrer sur des exemples spécifiques.

Thème 1: Que doivent savoir les élèves et comment ce qu’ils savent doit-il être structuré pour une résolution efficace des problèmes?

Nous commençons par identifier certains des différents types de connaissances que les étudiants doivent connaître:

• Connaissances conceptuelles, telles que le concept de momentum ou d’énergie, ou que la vitesse d’un objet change lorsqu’il accélère, ou que l’énergie potentielle gravitationnelle d’un objet diminue à mesure qu’il tombe.
• Connaissances factuelles, telles que la valeur de la constante gravitationnelle g, le rayon de la lune ou la densité du fer.
• Connaissances représentatives, telles que la façon de dessiner et d’utiliser des graphiques.
• Les connaissances stratégiques, telles que la capacité de reconnaître l’applicabilité d’un concept, comme l’élan est conservé lorsqu’il n’y a pas de forces extérieures, ou cette énergie est conservée lorsqu’il n’y a pas de forces non conservatrices.
• Connaissances méta-cognitives, par exemple, la conscience des hypothèses sous-jacentes, ou qu’une réponse doit être vérifiée en résolvant le problème d’une manière différente.
• Connaissance de soi, comme connaître ses sources probables d’erreurs, ou savoir qu’il faut être plus procédural lorsqu’on résout des problèmes.
• Connaissances opérationnelles, telles que comment prendre le produit croisé ou le produit scalaire de deux vecteurs, ou comment prendre le déterminant d’une matrice, ou comment dessiner un diagramme à corps libre.
• Connaissances procédurales, telles que le moment d’utiliser la conservation de l’énergie (p. ex., lorsque toutes les forces sont conservatrices), ou quand spécifier un système de coordonnées (par exemple, lors de la recherche d’énergie potentielle), ou quand dessiner un diagramme de corps libre (par exemple, lors de l’application des lois de Newton).
• Connaissance de l’état du problème, qui sont les caractéristiques d’un problème utilisé pour décider comment le résoudre. Les exemples sont: sachant qu’il n’y a pas de forces externes dans un problème particulier, ou qu’il n’y a pas de forces non conservatrices dans le problème, ou qu’un objet est au repos initialement, ou que l’objet est sur une pente.

Ces types de connaissances doivent être organisés et structurés pour une utilisation efficace lors de la résolution de problèmes. Afin de discuter des aspects organisationnels et structurels des connaissances, nous avons trouvé commode de classer ces types en trois catégories générales. Nous appelons ces trois groupes: La Connaissance Conceptuelle, la Connaissance Opérationnelle et Procédurale et la Connaissance de l’État du Problème. Sur la Fig. 1, ces trois catégories générales sont présentées dans une représentation de la façon dont les experts stockent les connaissances sur le contenu.

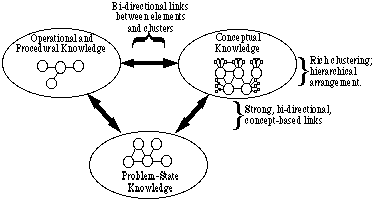Fig. 1: Une représentation de la structure des connaissances d’un expert

L’expert dispose d’un riche regroupement de concepts, dans lequel chaque concept est lié à de nombreux autres concepts, et les relations entre les concepts sont clairement comprises. Les concepts sont organisés hiérarchiquement à l’aide de concepts parapluie pour les relier plus étroitement. En fait, les concepts-cadres sont utilisés pour regrouper des éléments dans chacune des trois catégories. L’expert dispose d’une grande réserve de connaissances sur les problèmes, y compris de nombreuses informations sur les principes qui s’appliquent à des situations particulières. L’expert dispose également d’un grand nombre d’équations, d’opérations et de procédures (EOPs) accessibles rapidement.

Les liens entre chaque paire de catégories sont très forts : les états problématiques sont fortement liés aux concepts et aux EOP, qui sont eux-mêmes fortement liés les uns aux autres. Les mêmes concepts généraux sont utilisés pour regrouper les concepts, les états de problème et les POE. Par conséquent, pour tout problème particulier, des concepts peuvent être utilisés pour décider de la pertinence et de l’applicabilité des équations, et de l’utilité d’opérations et de procédures spécifiques.

(Il faut faire très attention ici à ne pas être trop rigide dans sa pensée, car il est facile de ne pas être d’accord sur laquelle de ces catégories doit être utilisée pour classer un élément particulier de la connaissance, ou si elle appartient à une seule catégorie. Notre but est simplement d’avoir un mécanisme pour visualiser les différents niveaux d’association qui peuvent se produire entre les éléments.)

Nous avons tendance à utiliser le terme de liaison pour désigner une association formée entre deux éléments de types de connaissances identiques ou différents, et le terme de regroupement pour désigner des associations entre plusieurs éléments ou clusters. Ce qui rend ce genre de discussion très difficile, c’est qu’il y a une sorte de processus itératif en cours ici: Un lien très fort entre trois éléments — un cluster conceptuel, la reconnaissance des circonstances rendant le concept applicable et les procédures nécessaires à son application — forme un nouveau type d’élément de connaissance que nous mettons dans la Connaissance stratégique (une quatrième catégorie). Ce nouvel élément de connaissance est ce que certains appellent un schéma et implique souvent également une connaissance de l’état du problème. Puisque l’élément de connaissance est de nature conceptuelle, il devient répliqué (c’est-à-dire répété) dans la bulle conceptuelle.

Si nous examinons de plus près la bulle conceptuelle, nous voyons certains types spécifiques de connaissances conceptuelles, par exemple, les Connaissances Représentationnelles, les Connaissances Stratégiques, les Connaissances Méta-Cognitives et la Connaissance des Concepts de Base. Ceci est représenté à la Fig. 2. (Les autres types de connaissances conceptuelles ne sont pas présentés.)

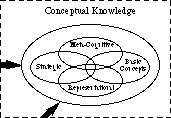Fig. 2: Types de connaissances conceptuelles

En quoi la structure des connaissances d’un novice est-elle différente de celle d’un expert? Comme représenté à la Fig. 3, les novices ont généralement un mauvais regroupement de concepts. De nombreux liens sont inappropriés; d’autres sont inexistants. Certains des liens inappropriés sont extrêmement forts, ce qui conduit à des idées fausses. Les novices n’utilisent généralement pas de concepts de parapluie pour regrouper des éléments. Ils ont une petite réserve de situations problématiques, dans lesquelles les caractéristiques de surface sont utilisées pour les regrouper et décider de la manière dont les problèmes doivent être résolus. Ils connaissent un nombre relativement important d’équations, mais ils s’en souviennent souvent incorrectement ou ont besoin de les rechercher pour les utiliser. On leur a enseigné les opérations et les procédures, mais ils ne les maîtrisent pas encore. Par conséquent, on ne peut pas dire qu’ils les « connaissent ».

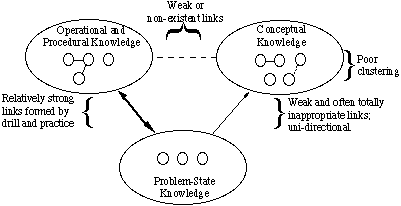Fig. 3: Une représentation de la structure des connaissances du novice

Les liens entre les concepts et les EOP sont faibles ou inexistants. Les liens entre les concepts et les situations problématiques sont également faibles. Ainsi, un novice ne peut pas analyser un problème et ne peut pas décider de la pertinence d’équations particulières. Les liens entre les situations problématiques et les POE sont relativement forts, mais les liens sont basés principalement sur les quantités que les équations ont en commun avec les données et les inconnues explicites du problème.

Thème 2: Dans quels types de processus cognitifs les élèves doivent-ils s’engager pour développer des structures de connaissances appropriées?

Pour répondre à cette question, il faut d’abord comprendre comment les experts et les novices résolvent les problèmes différemment.

Les novices échouent généralement lorsqu’ils tentent de résoudre des problèmes typiques de la physique. En utilisant le modèle pour représenter le processus, comment un novice typique résout-il un problème? Parce que les liens les plus forts dans la structure de la connaissance du novice sont entre les situations problématiques et les équations, la lecture d’un problème suggère immédiatement des équations impliquant les quantités (connues et inconnues) explicitement données dans le problème. Sans déterminer l’applicabilité de ces équations, et sans essayer de penser à d’autres équations qui pourraient impliquer les mêmes quantités, le novice commence généralement à manipuler les équations les plus familières jusqu’à ce que l’inconnu puisse être résolu. L’équation la plus récente couverte en classe est la plus facilement accessible et la plus rapidement rappelée. Ainsi, le novice cherche et (s’il « réussit ») ne trouve qu’un seul moyen de résoudre un problème et s’arrête généralement, sans étudier d’autres possibilités et sans analyser la situation problématique. Les équations trouvées de cette façon sont souvent inappropriées car les novices n’utilisent souvent pas de concepts pour justifier leur application. Même si les élèves sont amenés à invoquer des concepts en analysant les problèmes à l’avance, leurs liens avec les POE sont généralement trop faibles pour être utiles à la résolution de problèmes. De plus, les liens entre les concepts et les situations problématiques sont unidirectionnels, de sorte que les analogies ne sont pas particulièrement utiles: Les novices ne peuvent pas utiliser des analogies pour résoudre des problèmes car ils ne peuvent pas identifier lesquels des problèmes qu’ils ont déjà résolus sont conceptuellement similaires à celui qu’ils essaient actuellement de résoudre. Au lieu de cela, les novices utilisent des caractéristiques de surface pour établir une « similitude » et essayer de résoudre de nouveaux problèmes en fonction de leur similitude avec les caractéristiques de surface des problèmes qu’ils ont déjà résolus.

Parce que les experts classent les problèmes et les POE selon les mêmes concepts généraux, ils peuvent souvent passer directement des situations problématiques aux équations, opérations et / ou procédures appropriées. Parce que les liens entre les différentes catégories sont forts, les problèmes difficiles (ceux pour lesquels il n’existe pas encore de lien direct entre les États problématiques et les POE) peuvent être résolus en invoquant consciemment des concepts, reliant ainsi indirectement les États problématiques aux POE (s) appropriées. Parce que les liens entre les concepts et les situations problématiques sont bidirectionnels, les analogies sont un outil de résolution de problèmes extrêmement utile pour les experts. Enfin, les experts ont généralement plus d’une approche pour résoudre un problème particulier.

Voici un résumé des principales différences entre experts et novices:

1. Les novices ont un mauvais regroupement de concepts, ce qui conduit souvent à des idées fausses. Les experts disposent d’un riche regroupement de concepts, de situations problématiques, d’équations, de procédures et d’opérations, ce qui améliore la capacité de résolution de problèmes.
2. Les novices n’ont généralement qu’un seul moyen de résoudre un problème particulier, alors que les experts peuvent souvent trouver plus d’un moyen. Par conséquent, l’expert peut tenter de résoudre les incohérences lorsqu’elles se produisent et vérifier les réponses, tandis que les novices ignorent qu’il existe des incohérences et ne peuvent pas vérifier leurs réponses.
3. Les novices utilisent souvent la manipulation d’équations et utilisent rarement des stratégies basées sur des concepts pour obtenir une réponse. L’expert utilise des concepts et des analogies pour suggérer plusieurs méthodes de solution et planifie une stratégie pour trouver la bonne réponse.
4. Les novices ne parviennent souvent pas à obtenir la bonne réponse, et lorsqu’ils obtiennent la bonne réponse, cela peut facilement être pour la mauvaise raison. Lorsque le novice obtient la bonne réponse pour la mauvaise raison, les idées fausses sont renforcées et deviennent encore plus difficiles à surmonter. Un expert obtient généralement la bonne réponse et peut expliquer pourquoi la réponse est correcte.

Il existe une variété de processus cognitifs utiles pour aider les novices à développer une approche conceptuelle de résolution de problèmes, que nous divisons en trois catégories: Les Processus d’Analyse, les Processus de Raisonnement et les Processus Méta-cognitifs.

Processus d’analyse

• Analyse de problème, telle que la construction d’une représentation de problème.
• Analyse conceptuelle, telle que l’utilisation de concepts pour déterminer le comportement qualitatif d’objets physiques ou pour former une stratégie.
• Analyse stratégique, telle que l’identification et la justification des principes de physique pertinents à une situation problématique.
• Analyse de représentation, telle que l’exploration de différentes représentations d’un problème.
• Analyse constructive complexe, telle que la décomposition d’une situation complexe en une situation plus simple.

Processus de raisonnement

• Comparaison et contraste, par exemple en identifiant comment les éléments, les situations ou les conditions sont similaires et / ou différents.
• Interprétation, par exemple, en utilisant la forme d’un graphique de position vs. temps d’estimer l’accélération de l’objet.
• Cas spéciaux et limitatifs, c’est-à-dire explorant des conditions extrêmes et / ou connues.
• Prototypes et contre-exemples, par exemple, générant des catégories archétypales.
• Généralisation, c’est-à-dire reconnaître les caractéristiques saillantes d’une circonstance ou d’une situation.

Processus méta-cognitifs

• Réflexion, c’est-à-dire examen autogéré du but, des objectifs, des effets de l’expérience, etc.
• La méta-communication, qui est une participation consciente à l’établissement et au raffinage des lignes de communication avec l’enseignant et les autres élèves, et à la décision des objectifs de l’apprentissage.
• Auto-évaluation, telle que l’évaluation de sa performance ou l’identification des raisons pour lesquelles des difficultés ont été rencontrées lors de la résolution d’un problème.

Ces processus et d’autres sont encouragés par notre matériel pédagogique. Les types d’activités spécifiques pour ce faire sont présentés dans la section suivante.

Thème 3: Quels types d’activités ou d’expériences d’apprentissage favorisent ces processus cognitifs bénéfiques?

Les activités suivantes peuvent être utilisées par les enseignants pour stimuler les processus cognitifs nécessaires au développement d’une compréhension conceptuelle de la physique:

1. Utilisez plusieurs représentations. Une représentation peut être linguistique, abstraite, symbolique, picturale ou concrète. L’utilisation de nombreuses représentations différentes pour les mêmes connaissances et le fait que les élèves traduisent entre les représentations aident l’élève à relier les types de connaissances et à relier les connaissances à l’expérience physique. Il encourage la formation de liens entre les éléments de connaissance et favorise un regroupement riche de connaissances.
2. Faites des références avant et arrière. Les concepts nécessitent beaucoup de temps pour être formés. Ainsi, vous ne pouvez pas attendre que les élèves apprennent complètement un sujet avant de passer au suivant. En faisant des références à l’avance, vous préparez l’étudiant à de nouveaux matériaux. En faisant des références arriérées, vous associez du nouveau matériel à du matériel établi (ou partiellement établi), rendant ainsi les connaissances entrelacées et interconnectées, plutôt que linéaires.
3. Explorez des contextes étendus. Les concepts peuvent être extrêmement dépendants du contexte et ne deviennent globalement utiles que lorsqu’ils sont résumés. L’étude d’un vaste contexte d’applicabilité aide l’étudiant à affiner et à abstraire les concepts. Cela évite également les généralisations incorrectes ou simplifiées.
4. Comparer et contraster. La classification et l’interrelation des éléments de connaissance sont essentielles au processus de structuration (ou de restructuration) des connaissances. Les comparaisons et les contrastes sensibilisent les élèves aux catégories et aux relations, et les aident à percevoir les points communs et les distinctions nécessaires à l’organisation de leur réserve de connaissances.
5. Catégoriser et classer. Parallèlement aux comparaisons et aux contrastes, les élèves doivent connaître les catégories et les systèmes de classification. Les étudiants doivent également s’exercer à créer et à reconnaître des systèmes de catégorisation. En exigeant des élèves qu’ils classent des éléments, qu’ils choisissent des noms pour leurs catégories et qu’ils expliquent leur système, nous pouvons les aider à restructurer leur réserve de connaissances.
6. Prédire & Montrer (insuffisance de l’ancien modèle). Des démonstrations et des expériences soigneusement sélectionnées peuvent être utilisées pour mettre en évidence des incohérences dans les modèles des élèves. On devrait montrer aux élèves un appareil d’installation ou d’expérimentation et leur demander de prédire ce qui se passera lorsque quelque chose sera fait. Il est important que les élèves fassent des prédictions à l’avance, les sensibilisant ainsi à leur propre modèle. Les étudiants ne considéreront d’autres conceptions que si la leur échoue. Exiger des élèves qu’ils utilisent leurs modèles et leur montrer en quoi leurs modèles sont incohérents ou inadéquats les préparera à créer de meilleurs modèles (bien que toujours les leurs).

7. Expliquer (résumer, décrire, discuter, définir, etc.). Les problèmes standard disent rarement à l’enseignant ce que les élèves ne comprennent pas. Même lorsque les étudiants obtiennent un problème correct, il peut toujours y avoir une confusion quant à l’applicabilité des équations utilisées. Exiger des élèves qu’ils expliquent comment ils vont résoudre un problème expose les malentendus et les idées fausses, et aide les élèves à réorganiser leur réserve de connaissances. De plus, les étudiants voient rarement dans les démonstrations et les expériences standard ce que les experts voient. Les élèves doivent expliquer et discuter de ce qu’ils pensent avoir vu (lors de l’émission Predict &, par exemple), afin que l’enseignant puisse interagir avec les modèles des élèves. De plus, le processus d’explication (ou de synthèse, de description, de discussion, etc.) aide les élèves à prendre conscience de leurs propres modèles ainsi que des modèles des autres élèves.

8. Générez de multiples solutions. Une résolution efficace des problèmes ne peut se produire que si les étudiants choisissent parmi un ensemble de chemins de solution valides. En résolvant les problèmes de plus d’une manière, les élèves apprennent à hiérarchiser les éléments de leurs connaissances stratégiques.

9. Planifiez, justifiez et élaborez des stratégies. Très peu de relations en physique sont toujours valables. Pour éviter la manipulation d’équations, on devrait demander aux élèves de planifier (puis d’expliquer) comment ils vont résoudre les problèmes. Les élèves doivent apprendre à déterminer quels concepts sont pertinents (et lesquels ne sont pas pertinents) pour une situation problématique particulière et à mettre en œuvre les concepts pertinents pour résoudre ce problème. Le fait que les élèves génèrent leurs propres stratégies les aide à apprendre comment les concepts sont utilisés pour résoudre des problèmes.
10. Réfléchir (évaluer, intégrer, étendre, généraliser, etc.) Après avoir terminé la plupart des activités, les élèves bénéficient d’un retour sur ce qu’ils ont fait. Quels modèles ont-ils perçus? Quelles règles générales peuvent être construites? D’autres types d’activités donnent aux élèves les éléments nécessaires pour créer une image cohérente de la physique, mais une sorte d’activité réflexive est généralement nécessaire pour « assembler les éléments ».
11. Méta-communiquer sur le processus d’apprentissage. Pour apprendre la physique (ou tout autre sujet complexe), les étudiants doivent s’investir eux-mêmes. Ils doivent être exposés aux modèles des autres (enseignants et élèves). Ils doivent être avertis que la précision de la communication est essentielle; ils doivent être informés des pièges courants et des erreurs d’interprétation; et ils doivent être informés qu’ils doivent réorganiser leurs connaissances. Les élèves doivent apprendre comment ils apprennent le mieux.