a kinetikus energia a mozgás energiája. A kinetikus energia kifejezését úgy kapjuk meg, hogy megnézzük egy tárgy esetét, amelyet valamilyen relatív magasságra emelnek (így ezen a tárgyon munkát végeznek), majd hagyják esni.
kulcsfogalmak
o kinetikus energia
célok
o a kinetikus energia kifejezése a munka fizikai fogalmából
O megérteni a munka és a kinetikus energia kapcsolatát
O számítsuk ki a különböző tárgyak kinetikus energiáját
kezdjük!
a munka és a mozgási energia összefüggése
bizonyos értelemben a munka a feladatba (vagy talán “a tárgyba”) fektetett energia mennyisége. Képzeljük el például, hogy felveszünk egy tárgyat a padlóról, és felemeljük egy bizonyos magasságra; sokat dolgoztunk ezen a tárgyon. Ha azonban elengedjük, felgyorsul, mintha az a munka, amit a tárgy felemelésekor végeztünk, mozgásba lendülne. Ezen a példán keresztül levezethetjük a kinetikus energia definícióját, amely a mozgás energiája. Ez a meghatározás, amint látni fogjuk, szorosan kapcsolódik ahhoz, hogy miként határoztuk meg a munkát.
először Vegyünk egy tárgyat: egy m tömegű labdát. felvesszük a labdát az asztalról, és h távolságra emeljük az asztal fölé, az alábbiak szerint. Ezért W = mgh mennyiségű munkát végeztünk (ez az eredmény az elmozdulási vektor (h) és az alkalmazott erő (mg) nagyságának szorzata-a megfelelő Vektorok párhuzamosak).
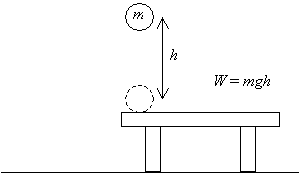
most, ha elengedjük a labdát, és hagyjuk, hogy leessen az asztal feletti h magasságból, amint visszatér az eredeti magasságába (az asztal szintjére), akkor egy bizonyos v sebessége lesz, amely a gravitáció miatti gyorsulás eredménye.
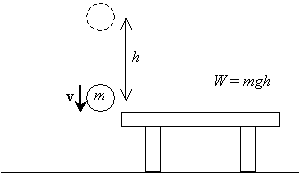
ki akarjuk számítani ezt a sebességet (vagy technikailag a sebességet-alkalmanként helyettesíthetjük a sebesség kifejezést a sebességgel, de mindig tisztában kell lennünk azzal, hogy a sebesség valójában egy vektor, a sebesség pedig a sebesség nagysága). Tudjuk, hogy a gravitáció miatti gyorsulás állandó, és hogy a labda kezdeti sebessége nulla (mozdulatlan, mielőtt elengedné). Feltételezzük, hogy a labda kezdeti magassága h, végső magassága pedig nulla (az asztal szintje). A sebesség kiszámításához a megfelelő képletek levezetésével elemi integrálszámítás használatát követeljük meg. (Ha haladó hallgató vagy, vagy extra kihívást keres, akkor megpróbálhatja ezeket a képleteket a fenti feltételek mellett levezetni. Egyszerűen vegye figyelembe, hogy a golyó v sebessége az X pozíciójának változásának időbeli sebessége a t idő függvényében, ![]() , és hogy az a gyorsulás a sebesség változásának időbeli sebessége,
, és hogy az a gyorsulás a sebesség változásának időbeli sebessége, ![]() .)
.)
![]()
![]()
ezek a képletek kifejezik a sebességet az idő függvényében, v (t), és a pozíciót(magasság) az idő függvényében, x (t), az a gyorsulás, a H magasság és a T idő szempontjából. A labda végső helyzete nulla méter, vagy x (t) = 0. Számítsuk ki a T-T, azt az időtartamot, amely a labda felszabadulása és az asztal szintjére való megérkezése között van.
![]()
![]()
![]()
most számítsuk ki a labda sebességét ebben az időben.
![]()
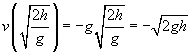
most hasonlítsuk össze ezt az eredményt az eredetileg az objektumon végzett munkával: W = mgh. Figyeljük meg, milyen szoros formában ez a két kifejezés; valójában, az egyetlen tényező hiányzik a sebesség a tömeg a labda, m. ha négyzetre a sebesség, szorozva m, majd osztva 2, akkor valójában ugyanaz a kifejezés, mint a munka!
![]()
így bizonyos értelemben láthatjuk, hogyan lehet levezetni a kinetikus energia meghatározását. A kinetikus energia K egy tárgy, akkor egy skalár az alábbiak szerint definiálva, ahol m a tárgy tömege, v pedig a sebessége:
![]()
mint kiderült, a kinetikus energia az a munka, amelyet egy tárgyon az adott tárgyra ható nettó erő végez. Így, bár egy nő bizonyos mennyiségű munkát végezhet egy tárgyon azáltal, hogy egyik magasságból a másikba emeli, az adott tárgyra ható nettó erő nulla (a nő a gravitáció irányában egyenlő, de ellentétes erőt alkalmaz). Így a kinetikus energia nem változik. Ha azonban ezt a tárgyat elengedik és hagyják leesni, kinetikus energiát nyer, mert a rá ható nettó erő egyszerűen a gravitáció (egyetlen erő). Így ahhoz, hogy megértsük a kinetikus energia és a munka kapcsolatát, kissé finomítanunk kell a munka fogalmát. Ha a W munkát úgy definiáljuk, mint az összes erő által a tárgyon végzett teljes munkát (más szóval a nettó erő által a tárgyon végzett munkát), akkor a W munka és a kezdeti és végső kinetikus energiák (Ki és Kf) között a következő kapcsolat áll fenn.
![]() ahol
ahol ![]()
így egy tárgyon végzett nettó munka megegyezik az adott tárgy mozgási energiájának változásával (ons). A következő gyakorlati problémák lehetőséget nyújtanak arra, hogy teszteljék és alkalmazzák a munka és a kinetikus energia fogalmainak megértését.
Gyakorlati Probléma: Az 1 kilogramm tömegű lövedék másodpercenként 5 méterrel halad. Milyen sebességgel kell haladnia egy 0,1 kilogrammos lövedéknek, hogy ugyanazt a kinetikus energiát elérje?
megoldás: először számítsuk ki a masszívabb (1 kilogramm) lövedék kinetikus energiáját.
![]()
most kiszámíthatjuk a kevésbé masszív tárgy sebességét úgy, hogy ugyanaz a kinetikus energiája legyen, K.
![]()
![]()
![]()
gyakorlati probléma: egy ember felemel egy 15 kilogrammos súlyt két méter magasra a talajtól, mielőtt ledobja. Abban a pillanatban, amikor a súly érintkezik a talajjal, mekkora a sebessége?
megoldás: rajzoljunk egy diagramot, amely bemutatja a tárgyra ható erőket, amikor felemelkedik és esik; ezek az erők magukban foglalják a gravitációt (Fg) és az ember által alkalmazott felfelé irányuló erőt (Fu).
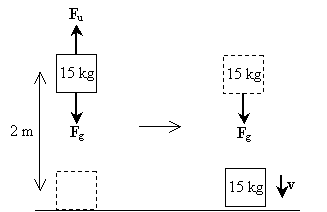
vegyük észre, hogy a folyamat első lépése (a súly felemelése) nem tartalmaz nettó erőt, amely a tárgyra hat-a gravitáció miatti erőt kiegyensúlyozza az az erő, amelyet az ember a súly felemelésekor alkalmaz. A második lépésben azonban a súly csak a gravitációs erőt tapasztalja meg. A nettó erő ebben az esetben tehát mg lefelé. Mint ilyen, az objektum sebessége is lefelé mutat. A gravitáció következtében a súlyon végzett munka egyszerűen mgh; ez a folyamat során a súlyon végzett teljes munka is. Vegye figyelembe, hogy a súly kezdeti kinetikus energiája nulla, mert nulla sebességgel rendelkezik. Most számítsuk ki a sebességet a nettó munka és a kinetikus energia változása közötti kapcsolat alkalmazásával.