Stacionaritás azt jelenti, hogy az idősorok statisztikai tulajdonságai, azaz az átlag, a variancia és a kovariancia nem változnak az idő múlásával. Sok statisztikai modell megköveteli, hogy a sorozat stacionárius legyen, hogy hatékony és pontos előrejelzéseket készítsen.
két statisztikai tesztet használnának egy idősoros Dickey Fuller (“ADF”) teszt és Kwiatkowski – Phillips-Schmidt-Shin (“KPSS”) teszt stacionaritásának ellenőrzésére. A nem helyhez kötött idősorok helyhez kötött sorozatokká történő átalakítására szolgáló módszert is alkalmazni kell.
ez az első cella szabványos csomagokat importál, és a diagramokat sorba állítja.
:
%matplotlib inlineimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport statsmodels.api as sm
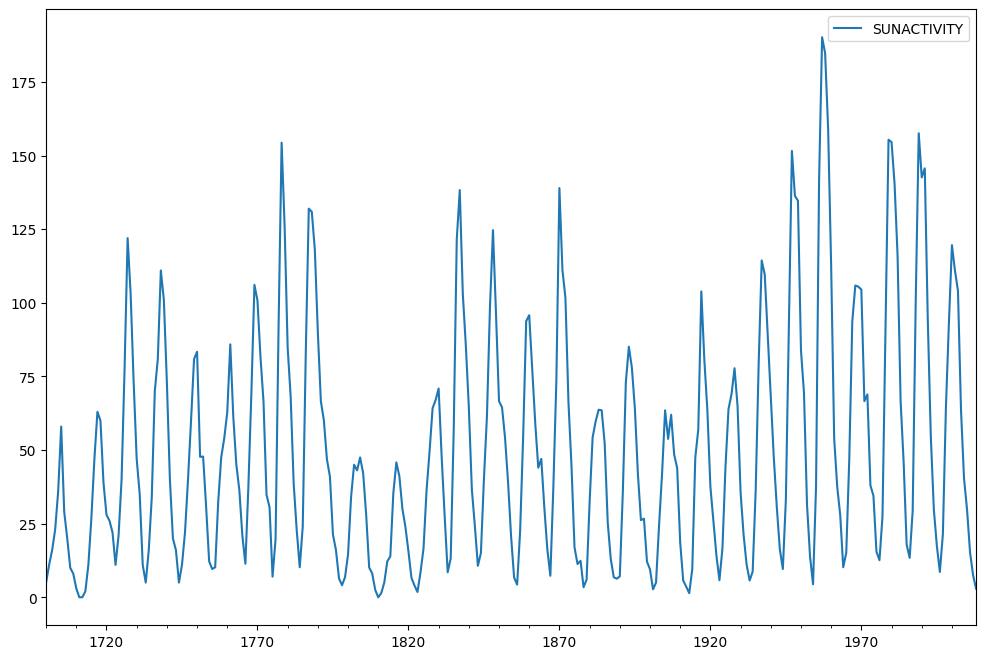
a napfoltok adatkészletét használják. Évente (1700-2008) adatokat tartalmaz a napfoltokról a Nemzeti Geofizikai adatközpont.
:
sunspots = sm.datasets.sunspots.load_pandas().data
néhány előfeldolgozás az adatokon történik. Az” év ” oszlopot az index létrehozásához használják.
:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))del sunspots
az adatok most vannak ábrázolva.
:
sunspots.plot(figsize=(12,8))
:
<AxesSubplot:>
az ADF-tesztet (ADF-teszt) a (z)
(ADF-teszt) arra használjuk, hogy meghatározzuk az egységgyök jelenlétét a sorozatban, és ezáltal segít megérteni, hogy a sorozat áll-e vagy sem. A teszt null és alternatív hipotézise a következő:
Null hipotézis: a sorozatnak egységgyöke van.
alternatív hipotézis: a sorozatnak nincs egységgyöke.
ha a nullhipotézist nem sikerült elutasítani, ez a teszt bizonyítékot szolgáltathat arra, hogy a sorozat nem helyhez kötött.
létrejön egy függvény az ADF teszt idősoron történő végrehajtására.
:
from statsmodels.tsa.stattools import adfullerdef adf_test(timeseries): print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC') dfoutput = pd.Series(dftest, index=) for key,value in dftest.items(): dfoutput = value print (dfoutput)
a KPSS teszt (kpss) egy másik teszt egy idősor stacionaritásának ellenőrzésére. A KPSS teszt null és alternatív hipotézise ellentétes az ADF teszttel.
nullhipotézis: a folyamat trend stacionárius.
alternatív hipotézis: a sorozatnak egységgyöke van (a sorozat nem álló).
létrejön egy függvény a KPSS teszt idősoron történő végrehajtására.
:
from statsmodels.tsa.stattools import kpssdef kpss_test(timeseries): print ('Results of KPSS Test:') kpsstest = kpss(timeseries, regression='c', nlags="auto") kpss_output = pd.Series(kpsstest, index=) for key,value in kpsstest.items(): kpss_output = value print (kpss_output)
az ADF-tesztek a következő eredményeket adják: tesztstatisztika, p-érték és a kritikus érték 1% – os, 5% – os és 10% – os konfidencia intervallumokban.
ADF tesztet alkalmaznak az adatokon.
:
adf_test(sunspots)
Results of Dickey-Fuller Test:Test Statistic -2.837781p-value 0.053076#Lags Used 8.000000Number of Observations Used 300.000000Critical Value (1%) -3.452337Critical Value (5%) -2.871223Critical Value (10%) -2.571929dtype: float64
a 0,05 szignifikancia szint és az ADF teszt p-értéke alapján a nullhipotézis nem utasítható el. Ezért a sorozat nem helyhez kötött.
a KPSS tesztek a következő eredményeket adják: tesztstatisztika, p érték és a kritikus érték 1% – os, 5% – os és 10% – os konfidencia intervallumokban.
KPSS teszt most alkalmazzák az adatokat.
:
kpss_test(sunspots)
Results of KPSS Test:Test Statistic 0.669866p-value 0.016285Lags Used 7.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
a 0,05 szignifikancia szint és a KPSS teszt p-értéke alapján bizonyíték van a nullhipotézis elutasítására az alternatíva javára. Ezért a sorozat nem helyhez kötött a KPSS teszt szerint.
mindig jobb mindkét tesztet alkalmazni, hogy biztosítható legyen, hogy a sorozat valóban álló legyen. A helyhez kötött tesztek alkalmazásának lehetséges eredményei a következők:
itt az ADF teszt és a KPSS teszt eredményeinek különbsége miatt arra lehet következtetni, hogy a sorozat trend stacionárius és nem szigorú stacionárius. A sorozat differenciálással vagy modell illesztéssel rontható.
Degrending által Differencinging GmbH
ez az egyik legegyszerűbb módszer a degrend egy idősor. Új sorozat jön létre, ahol az aktuális időlépés értékét az eredeti megfigyelés és az előző időlépés megfigyelése közötti különbségként számítják ki.
differenciálást alkalmaznak az adatokon, és az eredményt ábrázolják.
:
sunspots = sunspots - sunspots.shift(1)sunspots.dropna().plot(figsize=(12,8))
:
<AxesSubplot:>
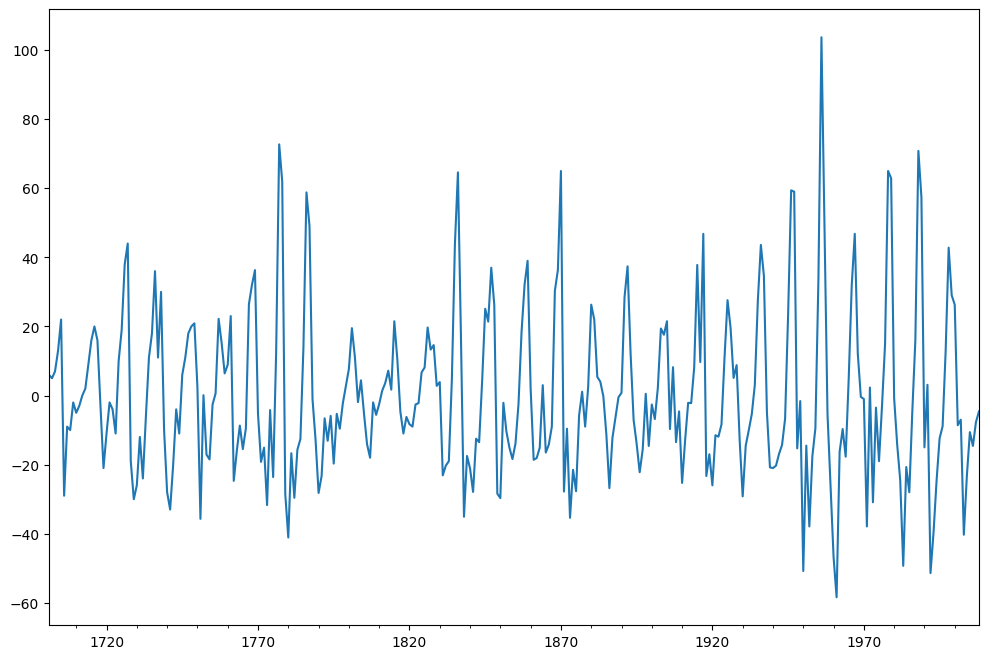
az ADF tesztet most alkalmazzák ezekre a detrended értékekre, és ellenőrzik a stacionaritást.
:
adf_test(sunspots.dropna())
Results of Dickey-Fuller Test:Test Statistic -1.486166e+01p-value 1.715552e-27#Lags Used 7.000000e+00Number of Observations Used 3.000000e+02Critical Value (1%) -3.452337e+00Critical Value (5%) -2.871223e+00Critical Value (10%) -2.571929e+00dtype: float64
az ADF teszt p-értéke alapján bizonyíték van a nullhipotézis elutasítására az alternatíva javára. Ezért a sorozat most szigorú helyhez kötött.
KPSS tesztet alkalmaznak ezekre a detrended értékekre, és ellenőrzik a stacionaritást.
:
kpss_test(sunspots.dropna())
Results of KPSS Test:Test Statistic 0.021193p-value 0.100000Lags Used 0.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/stattools.py:1911: InterpolationWarning: The test statistic is outside of the range of p-values available in thelook-up table. The actual p-value is greater than the p-value returned. warn_msg.format(direction="greater"), InterpolationWarning
a KPSS teszt p-értéke alapján a nullhipotézist nem lehet elutasítani. Ezért a sorozat helyhez kötött.
következtetés 6163>
egy idősor stacionaritásának ellenőrzésére két vizsgálatot alkalmaznak, nevezetesen az ADF-tesztet és a KPSS-tesztet. A Detrending differenciálás alkalmazásával történik. A Trend helyhez kötött idősorokat szigorú helyhez kötött idősorokká alakítják át. A szükséges előrejelzési modell most már alkalmazható egy álló idősoros adatokra.