the Basics: KNN for classification and regression

Data Science from the ground up

Data science or applied statistics tanfolyamok általában lineáris modellekkel kezdődnek, de a maga módján a K-legközelebbi szomszédok valószínűleg a legegyszerűbb széles körben használt modell fogalmilag. A KNN modellek valójában csak egy közös intuíció technikai megvalósításai, hogy a hasonló tulajdonságokkal rendelkező dolgok általában, jól, hasonló. Ez aligha mély betekintés, mégis ezek a gyakorlati megvalósítások rendkívül erősek lehetnek, és döntő fontosságú egy ismeretlen adatkészlethez közeledő személy számára, képes kezelni a nem-linearitásokat bonyolult adat-tervezés vagy modell felállítása nélkül.

mi

szemléltető példaként vegyük figyelembe a KNN modell osztályozóként történő használatának legegyszerűbb esetét. Tegyük fel, hogy vannak olyan adatpontok, amelyek a három osztály egyikébe tartoznak. Egy kétdimenziós példa így néz ki:

valószínűleg elég világosan láthatjuk, hogy a különböző osztályok csoportosítva vannak — a Grafikonok bal felső sarka úgy tűnik, hogy a narancssárga osztályhoz tartozik, a jobb oldali/középső szakasz a kék osztályhoz tartozik. Ha megkapnánk az új pont koordinátáit valahol a grafikonon, és megkérdeznénk, hogy valószínűleg melyik osztályba tartozik, a válasz legtöbbször elég egyértelmű lenne. A grafikon bal felső sarkában lévő bármely pont valószínűleg narancssárga, stb.

a feladat kevésbé biztos az osztályok között, ahol azonban döntési határon kell elhelyezkednünk. Vegye figyelembe az alábbi piros színnel hozzáadott új pontot:

ezt az új pontot narancssárgának vagy kéknek kell besorolni? Úgy tűnik, hogy a pont a két klaszter közé esik. Az első megérzésed az lehet, hogy azt a klasztert választod, amely közelebb áll az új ponthoz. Ez lenne a ‘legközelebbi szomszéd’ megközelítés, és annak ellenére, hogy fogalmilag egyszerű, gyakran elég ésszerű előrejelzéseket ad. Melyik korábban azonosított pont az új pont a legközelebb? Lehet, hogy nem nyilvánvaló, csak eyeballing a grafikon, mi a válasz, de ez könnyű a számítógép, hogy fut át a pontokat, és adjon nekünk egy választ:

úgy néz ki, mint a legközelebbi pont a kék kategóriában, így az új pont valószínűleg is. Ez a legközelebbi szomszéd módszer.

ezen a ponton elgondolkodhat azon, hogy mi a ‘k’ a K-legközelebbi szomszédokban. K a közeli pontok száma, amelyeket a modell egy új pont értékelésekor megvizsgál. A legegyszerűbb legközelebbi szomszéd példánkban ez a K értéke egyszerűen 1 volt — megnéztük a legközelebbi szomszédot, és ennyi volt. Lehet azonban úgy döntött, hogy nézd meg a legközelebbi 2 vagy 3 pont. Miért fontos ez, és miért állítana valaki k-t magasabb számra? Egyrészt az osztályok közötti határok egymás mellett ütközhetnek oly módon, hogy kevésbé nyilvánvaló, hogy a legközelebbi pont megadja nekünk a megfelelő besorolást. Vegyük példánkban a kék és zöld területeket. Valójában, nagyítsunk rájuk:

figyeljük meg, hogy míg a teljes régiók eléggé elkülönülnek, határaik kissé összefonódnak egymással. Ez az adatkészletek közös jellemzője, kis zajjal. Ebben az esetben nehezebbé válik a dolgok osztályozása a határterületeken. Fontolja meg ezt az új pontot:

egyrészt vizuálisan határozottan úgy néz ki, hogy a legközelebb korábban azonosított pont a kék, amelyet számítógépünk könnyen megerősíthet számunkra:

másrészt a legközelebbi kék pont kissé kiugrónak tűnik, messze a kék régió közepétől, és zöld pontokkal körülvéve. És ez az új pont még a kék pont külső oldalán is van! Mi lenne, ha megnéznénk az új piros ponthoz legközelebbi három pontot?

vagy akár az új ponthoz legközelebbi öt pontot?

most úgy tűnik, hogy új pontunk egy zöld környéken van! Véletlenül volt egy közeli kék pontja, de a túlsúly vagy a közeli pontok zöldek. Ebben az esetben talán lenne értelme magasabb értéket beállítani k-ra, megnézni egy maroknyi közeli pontot, és valahogy szavaztatni őket az új pont előrejelzéséről.

az illusztrált kérdés túlságosan illeszkedik. Ha k értéke egy, akkor az algoritmus által kékként és zöldként azonosított régiók közötti határ göröngyös, minden egyes ponttal előre kígyózik. A piros pont úgy néz ki, mintha a kék régióban lenne:

K-T 5-re emelve azonban kisimítja a döntési határt, amikor a különböző közeli pontok szavaznak. A piros pont most határozottan a zöld környéken tűnik:

a K magasabb értékeivel való kompromisszum a döntési határ granularitásának elvesztése. A k nagyon magas beállítása általában sima határokat ad, de a valós világ határai, amelyeket modellezni próbál, nem biztos, hogy tökéletesen simaak.

gyakorlatilag ugyanazt a legközelebbi szomszéd megközelítést alkalmazhatjuk a regressziókra, ahol egyéni értéket akarunk, nem pedig osztályozást. Tekintsük az alábbi regressziót:

az adatokat véletlenszerűen generáltuk, de lineárisnak állítottuk elő, így egy lineáris regressziós modell természetesen jól illeszkedik ezekhez az adatokhoz. Szeretnék rámutatni, bár, hogy a lineáris módszer eredményeit fogalmilag egyszerűbb módon közelítheti meg a K-legközelebbi szomszédok megközelítés. A regressziónk ebben az esetben nem egy olyan képlet lesz, mint amilyet egy OLS modell adna nekünk, hanem egy adott bemenet legjobban megjósolt kimeneti értéke. Tekintsük az értékét -.75 az x tengelyen, amelyet függőleges vonallal jelöltem meg:

egyenletek megoldása nélkül ésszerű közelítésre juthatunk ahhoz, hogy mi legyen a kimenet, csak a közeli pontok figyelembevételével:

logikus, hogy a megjósolt értéknek ezeknek a pontoknak a közelében kell lennie, nem sokkal alacsonyabb vagy magasabb. Talán jó előrejelzés lenne ezeknek a pontoknak az átlaga:

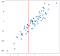
el lehet képzelni, hogy ezt az összes lehetséges bemeneti értéknél elvégezzük, és mindenhol előrejelzéseket kapunk:

ha ezeket az előrejelzéseket egy vonallal összekapcsoljuk, akkor regressziónk lesz:

ebben az esetben az eredmények nem tiszta vonal, de meglehetősen jól nyomon követik az adatok felfelé irányuló lejtését. Lehet, hogy ez nem tűnik rettenetesen lenyűgözőnek, de a megvalósítás egyszerűségének egyik előnye, hogy jól kezeli a nemlinearitást. Fontolja meg ezt az új pontgyűjteményt:

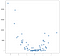
ezeket a pontokat az előző példa értékeinek egyszerű négyszögesítésével hozták létre, de tegyük fel, hogy egy ilyen adathalmazra bukkant a vadonban. Nyilvánvalóan nem lineáris jellegű, és bár egy OLS stílusú modell könnyen kezelheti az ilyen típusú adatokat, nemlineáris vagy interakciós kifejezések használatát igényli, vagyis az adattudósnak meg kell hoznia néhány döntést arról, hogy milyen adattechnikát végezzen. A KNN megközelítés nem igényel további döntéseket — ugyanaz a kód, amelyet a lineáris példában használtam, teljesen felhasználható az új adatokon, hogy működőképes előrejelzéseket kapjunk:

mint az osztályozó példáknál, a magasabb K érték beállítása segít elkerülni a overfit-et, bár előfordulhat, hogy elveszíti a prediktív erejét a margón, különösen az adatkészlet szélein. Tekintsük az első példa adatkészlet jóslatok készült k állítva egy, hogy a legközelebbi szomszéd megközelítés:

előrejelzéseink kiszámíthatatlanul ugrálnak, amikor a modell az adatkészlet egyik pontjáról a másikra ugrik. Ellentétben, beállítás k tízre, úgy, hogy tíz teljes pontot átlagoljunk együtt az előrejelzéshez, sokkal simább utazást eredményez:

általában ez jobban néz ki, de valami problémát láthat az adatok szélén. Mivel modellünk oly sok pontot vesz figyelembe az adott előrejelzésnél, amikor közelebb kerülünk a mintánk egyik széléhez, előrejelzéseink egyre rosszabbak lesznek. Ezt a kérdést némileg úgy kezelhetjük, hogy előrejelzéseinket a legközelebbi pontokra súlyozzuk, bár ez saját kompromisszumokkal jár.

hogyan

a KNN modell beállításakor csak néhány paramétert kell kiválasztani/módosítani a teljesítmény javítása érdekében.

K: a szomszédok száma: Amint azt megbeszéltük, a növekvő K hajlamos lesz elsimítani a döntési határokat, elkerülve a túlzott illeszkedést valamilyen felbontás árán. Nincs egyetlen K érték, amely minden egyes adatkészletnél működni fog. Osztályozási modelleknél, különösen, ha csak két osztály van, általában páratlan számot választanak k. ez azért van, hogy az algoritmus soha ne fusson ‘döntetlenbe’: pl. megnézi a legközelebbi négy pontot, és megállapítja, hogy közülük kettő a kék, kettő a piros kategóriába tartozik.

távolság metrikus: Mint kiderült, különböző módszerek vannak annak mérésére, hogy két pont mennyire ‘közel’ van egymáshoz, és a módszerek közötti különbségek magasabb dimenziókban jelentőssé válhatnak. A leggyakrabban használt euklideszi távolság, a szokásos rendezés, amelyet a középiskolában tanulhatott a Pitagorasz-tétel segítségével. Egy másik metrika az úgynevezett ‘Manhattan távolság’, amely az egyes bíboros irányokban megtett távolságot méri, nem pedig az átló mentén (mintha Manhattan egyik utcai kereszteződéséből a másikba sétálna, és az utcarácsot kellene követnie, ahelyett, hogy a legrövidebb’ légvonalban ‘ útvonalat választaná). Általánosabban, ezek valójában az úgynevezett Minkowski-távolság mindkét formája, amelynek képlete:

ha p értéke 1, Ez a képlet megegyezik a manhattani távolsággal, kettőre állítva pedig euklideszi távolság.

súlyok: az egyik módja annak, hogy megoldjuk mind a lehetséges ‘döntetlen’ kérdését, amikor az algoritmus egy osztályra szavaz, mind azt a kérdést, ahol a regressziós előrejelzéseink rosszabbodtak az adatkészlet szélei felé, a súlyozás bevezetésével. Súlyokkal a közeli pontok többet számítanak, mint a távolabbi pontok. Az algoritmus továbbra is megvizsgálja az összes k legközelebbi szomszédot, de a közelebbi szomszédoknak több szavazata lesz, mint a távolabbiaknak. Ez nem egy tökéletes megoldás, és felveti annak lehetőségét, overfitting újra. Tekintsük a regressziós példát, ezúttal súlyokkal:

előrejelzéseink most az adatkészlet szélére mennek, de láthatjuk, hogy előrejelzéseink most sokkal közelebb lendülnek az egyes pontokhoz. A súlyozott módszer meglehetősen jól működik, ha pontok között vagy, de ahogy egyre közelebb kerülsz egy adott ponthoz, az adott pont értéke egyre inkább befolyásolja az algoritmus előrejelzését. Ha elég közel kerülsz egy ponthoz, az majdnem olyan, mintha k-t állítanánk egyre, mivel ennek a pontnak annyi befolyása van.

méretezés/normalizálás: egy utolsó, de döntő fontosságú pont az, hogy a KNN modellek eldobhatók, ha a különböző jellemzőváltozók nagyon eltérő skálával rendelkeznek. Vegyünk egy modellt, amely megpróbálja megjósolni, mondjuk, egy ház eladási árát a piacon olyan jellemzők alapján, mint a hálószobák száma és a ház teljes alapterülete stb. A ház négyzetméterének száma nagyobb eltérést mutat, mint a hálószobák száma. Általában a házak csak egy kis maroknyi hálószobával rendelkeznek, és még a legnagyobb kastélyban sem lesz több tíz vagy száz hálószoba. Négyzetláb, másrészt, viszonylag kicsi, így házak terjedhet közel, mondjuk, 1000 sq feat A Kis oldalon, hogy több tízezer sq láb a nagy oldalon.

fontolja meg az összehasonlítást egy 2000 négyzetméteres ház 2 hálószobával és egy 2010 négyzetméteres ház két hálószobával-10 négyzetméter. láb alig tesz különbséget. Ezzel szemben egy 2000 négyzetméteres, három hálószobás ház nagyon eltérő, és nagyon eltérő és esetleg szűkebb elrendezést képvisel. Egy naiv számítógép azonban nem lenne képes megérteni ezt a kontextust. Azt mondaná, hogy az 3 hálószoba csak egy egységre van az 2 hálószobától, míg az 2,010 sq lábléc tízre van az 2,000 sq lábléctől. Ennek elkerülése érdekében a jellemzőadatokat a KNN modell bevezetése előtt méretezni kell.

erősségek és gyengeségek

a KNN modellek könnyen megvalósíthatók és jól kezelik a nem-linearitást. A modell illesztése szintén gyors: a számítógépnek végül nem kell kiszámítania semmilyen konkrét paramétert vagy értéket. A kompromisszum itt az, hogy míg a modell gyorsan beállítható, lassabb megjósolni, mivel az új érték kimenetelének előrejelzéséhez át kell keresnie a képzési készlet összes pontját, hogy megtalálja a legközelebbieket. Nagy adatkészletek esetén a KNN tehát viszonylag lassú módszer lehet más regressziókhoz képest, amelyek illeszkedése hosszabb ideig tarthat, de viszonylag egyszerű számításokkal teszik meg előrejelzéseiket.

a KNN modell másik problémája az, hogy nem értelmezhető. Az OLS lineáris regressziónak egyértelműen értelmezhető együtthatói lesznek, amelyek maguk is adhatnak némi jelzést az adott tulajdonság’ hatásméretéről ‘ (bár az ok-okozati összefüggés hozzárendelésekor némi óvatosságra van szükség). A KNN modell számára azonban nem igazán van értelme megkérdezni, hogy mely funkcióknak van a legnagyobb hatása. Részben emiatt a KNN modelleket nem igazán lehet használni a funkciók kiválasztására, oly módon, hogy egy lineáris regresszió hozzáadott költségfüggvény-kifejezéssel, mint a gerinc vagy a lasso, lehet, vagy ahogyan egy döntési fa implicit módon választja ki, mely funkciók tűnnek a legértékesebbnek.