Tudásstruktúra

a középiskolai Természettudományi tanárok műhelyét kísérő füzetből nyerték ki.

írta: Robert J. Dufresne, William J. Leonard és William J. Gerace

csoportunk az UMass-nál kifejlesztett egy kognitív modellt, amely segít bemutatni a különbségeket abban, ahogyan a szakértők és a kezdők tárolják és használják a tartalmi ismereteket. A modell segít abban is, hogy olyan konkrét területeket célozzunk meg, amelyekre az újoncoknak koncentrálniuk kell ahhoz, hogy jobb problémamegoldókká váljanak. A modell azonban csak egy reprezentációja a tudás struktúrájának, és folyamatosan fejlődik. Ezért nem szabad túl szó szerint venni. Hasznossága abból fakad, hogy képes konkrét megnyilvánulást nyújtani, bár tökéletlen, a szakértők és a kezdők gondolkodásmódjáról. A modell segít megvitatni:

1. a domain-specifikus tudás tárolása;
2. szakértő-és kezdő-szerű problémamegoldó viselkedés;
3. a szakértői tudástár hierarchikus felépítése;
4. tévhitek;
5. a cél nélküli és célirányos kérdések hatásai; és
6. a metakommunikációs folyamat.

ebben a műhelyben- – – és a fizika általános megközelítésében – – – 3 alapvető téma van:

1. a tudás és a tudásstruktúrák speciális típusaira van szükség a hozzáértő problémamegoldáshoz. E tudás nagy része fogalmi jellegű, szemben az operatív vagy eljárási jellegű ismeretekkel, és az erőteljes tudásszerkezetek szükségszerűen fogalmi elemeket tartalmaznak. A fogalmi elemek jelenléte a tudásstruktúrákban a fizika “mélyebb megértésének” kulcsa.
2. bizonyos típusú kognitív folyamatok szükségesek a fogalmi ismeretek megszerzéséhez és a hasznos tudásstruktúrák felépítéséhez.
3. lehetőség van olyan tevékenységek megtervezésére, amelyek elősegítik ezeket a kívánatos kognitív folyamatokat. Sok esetben ezek a tevékenységek egyszerűen maguk a kognitív folyamatok aktualizálásai. (Ez a kérdés remélhetőleg később világosabbá válik.)

ezeket a témákat részletezzük, mielőtt konkrét példákra összpontosítanánk.

1. Téma: mit kell tudni a hallgatóknak, és hogyan kell strukturálni azt, amit tudnak a hatékony problémamegoldás érdekében?

kezdjük azzal, hogy azonosítjuk azokat a különféle típusú ismereteket, amelyeket a hallgatóknak ismerniük kell:

• fogalmi tudás, például a lendület vagy az energia fogalma, vagy hogy egy tárgy sebessége megváltozik, amikor felgyorsul, vagy hogy egy tárgy gravitációs potenciális energiája csökken, Amikor esik.
• tényszerű ismeretek, például a G gravitációs állandó értéke, a Hold sugara vagy a vas sűrűsége.
• Reprezentációs ismeretek, például grafikonok rajzolása és használata.
• stratégiai ismeretek, például egy fogalom alkalmazhatóságának felismerésének képessége, például a lendület akkor konzerválódik, ha nincsenek külső erők, vagy hogy az energia konzerválódik, ha nincsenek nem konzervatív erők.
• metakognitív tudás, például az alapul szolgáló feltételezések tudatossága, vagy hogy a választ a probléma más módon történő megoldásával kell ellenőrizni.
• önismeret, például a hibák valószínű forrásának ismerete, vagy annak ismerete, hogy a problémák megoldása során eljárásibbnak kell lennie.
• működési ismeretek, például hogyan kell két vektor kereszttermékét vagy ponttermékét venni, vagy hogyan kell egy mátrix determinánsát venni, vagy hogyan kell rajzolni egy szabad test diagramot.
• eljárási ismeretek, például mikor kell használni az energiamegtakarítást (pl., amikor minden erő konzervatív), vagy mikor kell meghatározni a koordináta-rendszer (például a potenciális energia megtalálásakor), vagy mikor kell rajzolni a szabad test diagram (például Newton törvényeinek alkalmazásakor).
• probléma-államismeret, amelyek a probléma megoldásának eldöntéséhez használt probléma jellemzői. Példák: tudva, hogy egy adott problémában nincsenek külső erők, vagy hogy a problémában nincsenek nem konzervatív erők, vagy hogy egy tárgy kezdetben nyugalomban van, vagy hogy az objektum lejtőn van.

az ilyen típusú ismereteket szervezni és strukturálni kell a problémamegoldás hatékony felhasználása érdekében. A tudás szervezeti és strukturális szempontjainak megvitatása érdekében kényelmesnek találtuk ezeket a típusokat három általános kategóriába sorolni. Ezt a három csoportot nevezzük: fogalmi tudás, működési és eljárási tudás, valamint probléma-állapot tudás. Ábra. 1, Ez a három általános kategória A szakértők tartalmi ismeretek tárolásának ábrázolásában jelenik meg.

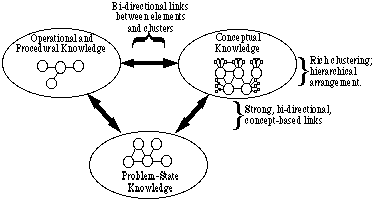ábra. 1: A szakértő tudásszerkezetének ábrázolása

a szakértőnek gazdag fogalomcsoportja van, amelyben minden fogalom sok más fogalomhoz kapcsolódik, és a fogalmak közötti kapcsolatok világosan érthetők. A fogalmak hierarchikusan vannak elrendezve az esernyő fogalmak segítségével, hogy szorosabban összekapcsolják őket. Valójában az esernyő fogalmakat az elemek csoportosítására használják a három kategória mindegyikén belül. A szakértőnek nagy mennyiségű probléma-állami ismerete van, beleértve sok információt arról, hogy mely elvek vonatkoznak az adott helyzetekre. A szakértő is van egy nagy áruház egyenletek, műveletek és eljárások (EOPs), hogy gyorsan elérhető.

az egyes kategóriapárok közötti kapcsolatok nagyon erősek: a problémás állapotok szorosan kapcsolódnak a fogalmakhoz és az EOP-khoz, amelyek maguk is szorosan kapcsolódnak egymáshoz. Ugyanazokat az ernyőfogalmakat használják a fogalmak, a problémás állapotok és az EOP-k csoportosítására. Ezért bármely konkrét probléma esetén a fogalmak felhasználhatók az egyenletek megfelelőségének és alkalmazhatóságának, valamint az egyes műveletek és eljárások hasznosságának eldöntésére.

(itt nagyon óvatosnak kell lennünk, hogy ne legyünk túl merevek a gondolkodásban, mert könnyű nem érteni egyet abban, hogy e kategóriák közül melyiket kell használni a tudás egy adott elemének osztályozására, vagy hogy csak egy kategóriába tartozik-e. Célunk egyszerűen egy mechanizmus létrehozása az egyes elemek közötti asszociáció több szintjének vizualizálására.)

hajlamosak vagyunk arra, hogy az összekapcsolás kifejezést az azonos vagy különböző tudástípusok két eleme közötti kialakult asszociációra, a klaszterezés kifejezést pedig több elem vagy klaszter közötti asszociációra utaljuk. Mi teszi ezt a fajta vita nagyon nehéz, hogy van egyfajta iteratív folyamat folyik itt: A három elem-a fogalmi klaszter, a fogalmat alkalmazhatóvá tevő körülmények felismerése és a koncepció alkalmazásához szükséges eljárások-közötti nagyon erős kötelék egy új típusú tudáselemet alkot, amelyet stratégiai tudásba (negyedik kategóriába) helyezünk. Ez az új tudáselem az, amit egyesek sémának neveznek, és gyakran magában foglalja a probléma-állapot tudást is. Mivel a tudáselem fogalmi jellegű, a fogalmi buborékban replikálódik (azaz megismétlődik).

ha közelebbről megvizsgáljuk a fogalmi buborékot, akkor a fogalmi tudás bizonyos típusait látjuk, például a Reprezentációs tudást, a stratégiai tudást, a metakognitív tudást és az alapfogalmak ismeretét. Ez az ábrán látható. 2. (Más típusú fogalmi ismeretek nem jelennek meg.)

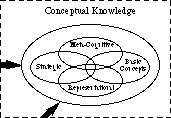Fig. 2: A fogalmi tudás típusai

miben különbözik a kezdő tudásszerkezete a szakértőtől? Amint az ábrán látható. 3, az újoncok általában rosszul csoportosítják a fogalmakat. Sok link nem megfelelő; mások nem léteznek. Néhány nem megfelelő kapcsolat rendkívül erős, ami tévhitekhez vezet. A kezdők általában nem használnak esernyő fogalmakat az elemek csoportosításához. Van egy kis tárolójuk a problémás helyzetekről, amelyekben a felületi jellemzőket arra használják, hogy összegyűjtsék őket, és eldöntsék, hogyan kell megoldani a problémákat. Viszonylag sok egyenletet ismernek, de gyakran helytelenül emlékeznek rájuk, vagy fel kell keresniük őket, hogy felhasználhassák őket. Megtanították őket műveletekre és eljárásokra, de még nem jártasak bennük. Ezért nem lehet azt mondani, hogy “ismerik” őket.

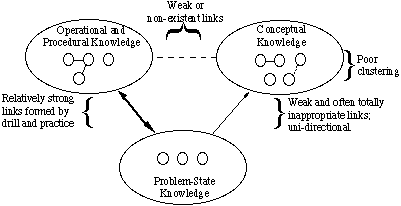ábra. 3: a novícius tudásszerkezetének ábrázolása

a fogalmak és az EOPs közötti kapcsolatok gyengék vagy nem léteznek. A fogalmak és a problémás helyzetek közötti kapcsolatok szintén gyengék. Így a kezdő nem tudja elemezni a problémát, és nem tudja eldönteni az egyes egyenletek megfelelőségét. A problémás helyzetek és az EOP-K közötti kapcsolatok viszonylag erősek, de a kapcsolatok elsősorban azon mennyiségeken alapulnak, amelyek az egyenletekben közösek a probléma adottságaival és explicit ismeretlenjeivel.

2. téma: Milyen kognitív folyamatokban kell a hallgatóknak részt venniük a megfelelő tudásstruktúrák kialakításában?

a kérdés megválaszolásához először meg kell értenünk, hogy a szakértők és a kezdők hogyan oldják meg másképp a problémákat.

a kezdők általában sikertelenek, amikor megpróbálják megoldani a fizika tipikus problémáit. Ha a modellt használja a folyamat ábrázolására, hogyan oldja meg egy tipikus kezdő a problémát? Mivel a kezdő tudásszerkezetében a legerősebb kapcsolat a problémás helyzetek és az egyenletek között van,a probléma olvasása azonnal egyenleteket javasol a problémában kifejezetten megadott (ismert és ismeretlen) mennyiségekkel. Anélkül, hogy meghatározná ezen egyenletek alkalmazhatóságát, és anélkül, hogy megpróbálna más egyenletekre gondolni, amelyek azonos mennyiségeket tartalmazhatnak, a kezdő általában elkezdi manipulálni a legismertebb egyenleteket, amíg az Ismeretlen meg nem oldható. Az osztályban szereplő legfrissebb egyenlet a legkönnyebben elérhető és a leggyorsabban visszahívható. Így a kezdő keresi és (ha “sikeres”) csak egy módot talál a probléma megoldására, és általában megáll, anélkül, hogy más lehetőségeket vizsgálna és elemezné a problémás helyzetet. Az így talált egyenletek gyakran nem megfelelőek, mert a kezdők gyakran nem használnak fogalmakat alkalmazásuk igazolására. Még akkor is, ha a diákokat arra késztetik, hogy a problémák előzetes elemzésével fogalmakat idézzenek elő, az EOP-khoz fűződő kapcsolataik általában túl gyengék ahhoz, hogy hasznosak legyenek a problémamegoldásban. Továbbá a fogalmak és a problémás helyzetek közötti kapcsolatok egyirányúak, így az analógiák nem különösebben hasznosak: A kezdők nem használhatnak analógiákat a problémák megoldására, mert nem tudják azonosítani, hogy a már megoldott problémák közül melyik fogalmi szempontból hasonló ahhoz, amelyet jelenleg próbálnak megoldani. Ehelyett a kezdők a felszíni jellemzőket használják a “hasonlóság” megállapítására, és megpróbálják megoldani az új problémákat a már megoldott problémák felületi jellemzőihez való hasonlóságuk alapján.

mivel a szakértők a problémákat és az EOP-kat ugyanazon ernyőfogalmak szerint osztályozzák, gyakran közvetlenül a problémás helyzetektől a megfelelő egyenletekig, műveletekig és/vagy eljárásokig mennek. Mivel a különböző kategóriák közötti kapcsolatok erősek, a nehéz problémák (amelyek esetében a problémás állapotok és az EOPs közötti közvetlen kapcsolat még nem létezik) tudatosan fogalmak hivatkozásával oldhatók meg, ezáltal közvetetten összekapcsolva a problémás állapotokat a megfelelő EOP(OK) val. Mivel a fogalmak és a problémás helyzetek közötti kapcsolatok kétirányúak, az analógiák rendkívül hasznos problémamegoldó eszköz a szakértők számára. Végül a szakértők általában egynél több megközelítést alkalmaznak egy adott probléma megoldására.

itt egy összefoglaló a szakértők és a kezdők közötti főbb különbségekről:

1. az újoncok gyengén csoportosítják a fogalmakat, ami gyakran téves elképzelésekhez vezet. Szakértők gazdag klaszterezés fogalmak, problémás helyzetek, egyenletek, eljárások és műveletek, ami jobb problémamegoldó képesség.
2. a kezdőknek általában csak egy módja van egy adott probléma megoldására, míg a szakértők gyakran egynél több módot találnak. Ezért a szakértő megkísérelheti megoldani a következetlenségeket, amikor azok előfordulnak, és ellenőrizheti a válaszokat, míg a kezdők nem tudják, hogy következetlenségek léteznek, és nem tudják ellenőrizni a válaszokat.
3. a kezdők gyakran használnak egyenletmanipulációt, és ritkán használnak koncepcióalapú stratégiákat a válasz megszerzéséhez. A szakértő fogalmakat és analógiákat használ, hogy több megoldási módszert javasoljon, és stratégiát tervez a helyes válasz megtalálására.
4. az újoncok gyakran nem kapják meg a helyes választ, és amikor megkapják a helyes választ, könnyen lehet, hogy rossz okból. Amikor a kezdő rossz okból megkapja a helyes választ, a tévhitek megerősödnek, és még nehezebbé válnak legyőzni. A szakértő általában megkapja a helyes választ, és meg tudja magyarázni, miért helyes a válasz.

számos kognitív folyamat segíti a kezdőket egy koncepció-alapú problémamegoldó megközelítés kidolgozásában, amelyet három kategóriába osztunk: elemzési folyamatok, érvelési folyamatok és Meta-kognitív folyamatok.

elemzési folyamatok

• Problémaelemzés, például problémamegjelenítés készítése.
• fogalmi elemzés, például fogalmak használata a fizikai tárgyak kvalitatív viselkedésének meghatározására vagy stratégia kialakítására.
• stratégiai elemzés, például a problémás helyzet szempontjából releváns fizikai elvek azonosítása és igazolása.
• Reprezentációs elemzés, például egy probléma különböző reprezentációinak feltárása.
• komplex konstruktív elemzés, például egy összetett helyzet egyszerűbbé bontása.

érvelési folyamatok

• összehasonlítás és kontraszt, például annak meghatározása, hogy az elemek, helyzetek vagy feltételek hasonlóak és/vagy eltérőek.
• tolmácsolás, például a helyzet ábrázolásának alakja vs. ideje megbecsülni az objektum gyorsulását.
• speciális és korlátozó esetek, azaz extrém és/vagy ismert körülmények feltárása.
• prototípus és ellenpéldák, például archetipikus kategóriák létrehozása.
• általánosítás, vagyis egy körülmény vagy helyzet kiemelkedő jellemzőinek felismerése.

metakognitív folyamatok

• reflexió, vagyis a cél, a célok, a tapasztalatok hatásainak önirányított áttekintése stb.
• metakommunikáció, amely tudatos részvétel a tanárral és a többi tanulóval való kommunikációs vonalak kialakításában és finomításában, valamint a tanulás céljainak eldöntésében.
• önértékelés, például a teljesítmény értékelése vagy annak azonosítása, hogy miért merültek fel nehézségek a probléma megoldása során.

ezeket és más folyamatokat a tananyagaink ösztönzik. Az ehhez szükséges tevékenységek konkrét típusait a következő szakasz mutatja be.

3. téma: Milyen típusú tanulási tevékenységek vagy tapasztalatok elősegítik ezeket a jótékony kognitív folyamatokat?

a tanárok a következő tevékenységeket használhatják a fizika fogalmi megértésének kialakításához szükséges kognitív folyamatok stimulálására:

1. használjon több ábrázolást. Az ábrázolás lehet nyelvi, absztrakt, szimbolikus, képi vagy konkrét. Sok különböző reprezentáció használata ugyanarra a tudásra, és a diákok lefordítása a reprezentációk között segít a hallgatónak a tudástípusok összekapcsolásában és a tudás fizikai tapasztalatokkal való összekapcsolásában. Ösztönzi a tudáselemek közötti kapcsolatok kialakulását és elősegíti a tudás gazdag csoportosulását.
2. tegyen előre és hátra hivatkozásokat. A fogalmak kialakítása hosszú időt igényel. Így nem várhatja meg, hogy a hallgatók teljesen megtanulják az egyik témát, mielőtt továbblépnének a másikra. Azáltal, hogy előre referenciák, előkészíti a hallgató az új anyag. Visszafelé történő hivatkozásokkal új anyagot társít a megalapozott (vagy részben megalapozott) anyaghoz, így a tudás összefonódik és összekapcsolódik, nem pedig lineáris.
3. fedezze fel a kiterjesztett kontextusokat. A fogalmak rendkívül kontextusfüggőek lehetnek, és csak akkor válnak globálisan hasznossá, ha elvontak. Az alkalmazhatóság széles kontextusának vizsgálata segít a hallgatónak finomítani és elvont fogalmakat. Ezenkívül elkerüli a helytelen vagy túl leegyszerűsített általánosításokat.
4. összehasonlítás és kontraszt. A tudás strukturálásának (vagy átstrukturálásának) folyamatában elengedhetetlen a tudáselemek osztályozása és egymáshoz való viszonya. Az összehasonlítások és ellentétek érzékennyé teszik a hallgatókat a kategóriákra és a kapcsolatokra, és segítik a tanulókat a Tudástár megszervezéséhez szükséges közös vonások és megkülönböztetések észlelésében.
5. kategorizálás és osztályozás. Az összehasonlításokkal és ellentétekkel párhuzamosan a hallgatóknak tisztában kell lenniük a kategóriákkal és az osztályozási rendszerekkel. A hallgatóknak gyakorolniuk kell a kategorizálási rendszerek létrehozását és felismerését is. Azáltal, hogy megköveteljük a hallgatóktól az elemek osztályozását, a kategóriák nevének kiválasztását és a rendszerük magyarázatát, segíthetünk a hallgatóknak a tudástáruk újraszervezésében.
6. Predict & Show (a régi modell elégtelensége). A gondosan kiválasztott demonstrációk és kísérletek felhasználhatók a hallgatói modellek következetlenségeinek feltárására. A diákokat fel kell mutatni egy felállított vagy kísérleti készüléknek, és meg kell kérni, hogy megjósolják, mi fog történni, ha valami történik. Fontos, hogy a hallgatók előzetesen előrejelzéseket tegyenek, ezáltal tudatosítsák saját modelljüket. A hallgatók csak akkor veszik figyelembe az alternatív elképzeléseket, ha a sajátjuk kudarcot vall. Ha a diákok megkövetelik, hogy használják modelljeiket, és megmutatják nekik, hogy modelljeik inkonzisztensek vagy nem megfelelőek, felkészítik őket arra, hogy jobb (bár még mindig saját) modelleket hozzanak létre.

7. magyarázza el (foglalja össze, írja le, beszélje meg, határozza meg stb.). A szokásos problémák ritkán mondják el a tanárnak, amit a diákok nem értenek. Még akkor is, ha a hallgatók jól kezelik a problémát, továbbra is zavart okozhat az alkalmazott egyenletek alkalmazhatósága. Ha a tanulókat arra kérik, hogy magyarázzák meg, hogyan oldják meg a problémát, félreértéseket és tévhiteket tár fel, és segít a hallgatóknak a tudástáruk átszervezésében. Ezenkívül a diákok ritkán látják a szokásos demonstrációkban és kísérletekben azt, amit a szakértők látnak. A diákoknak el kell magyarázniuk és meg kell vitatniuk, hogy mit láttak (például a Predict & Show alatt), hogy a tanár kölcsönhatásba léphessen a diákok modelljeivel. Ezenkívül a magyarázat (vagy összefoglalás, leírás, megbeszélés stb.) segít a hallgatóknak megismerni saját modelljeiket, valamint más hallgatók modelljeit.

8. több megoldás létrehozása. Hatékony problémamegoldás csak akkor fordulhat elő, ha a hallgatók érvényes megoldási útvonalak közül választanak. A problémák egynél több módon történő megoldásával a hallgatók megtanulják prioritásként kezelni stratégiai tudásuk elemeit.

9. terv, indoklás és stratégia. A fizikában nagyon kevés kapcsolat mindig érvényes. Az egyenletmanipuláció elkerülése érdekében a hallgatókat fel kell kérni, hogy tervezzék meg (majd magyarázzák el), hogyan oldják meg a problémákat. A hallgatóknak meg kell tanulniuk, hogyan lehet meghatározni, hogy mely fogalmak relevánsak (és amelyek irrelevánsak) egy adott problémás helyzethez, és hogyan kell végrehajtani a vonatkozó fogalmakat a probléma megoldásához. Ha a hallgatók saját stratégiákat készítenek, akkor megtanulják, hogyan használják a fogalmakat a problémák megoldására.
10. tükrözze (értékelje, integrálja, bővítse, általánosítsa stb.) A legtöbb tevékenység elvégzése után a hallgatók profitálnak abból, hogy visszatekintenek arra, amit tettek. Milyen mintákat érzékeltek? Milyen általános szabályokat lehet kialakítani? Más típusú tevékenységek megadják a hallgatóknak a fizika koherens képének létrehozásához szükséges darabokat, de általában valamilyen reflektív tevékenységre van szükség a “darabok összerakásához”.
11. Meta-kommunikáció a tanulási folyamatról. A fizika (vagy bármely más összetett tantárgy) megtanulásához a hallgatóknak önbefektetővé kell válniuk. Ki kell téve más emberek (tanár és diák) modelljeinek. Figyelmeztetni kell őket, hogy a kommunikáció pontossága elengedhetetlen; tájékoztatni kell őket a gyakori buktatókról és félreértelmezésekről; és meg kell mondani nekik, hogy újra kell strukturálniuk tudásukat. A diákoknak meg kell tanulniuk, hogyan tanulnak a legjobban.