L’energia cinetica è l’energia del movimento. Un’espressione per l’energia cinetica è derivata osservando il caso di un oggetto che viene sollevato ad una certa altezza relativa (quindi, il lavoro è fatto su questo oggetto) e quindi lasciato cadere.
Termini Chiave
o energia Cinetica
Obiettivi
o Ricavare un’espressione per l’energia cinetica del concetto della fisica del lavoro
o Capire il rapporto di lavoro e l’energia cinetica
o Calcolare l’energia cinetica di vari oggetti
iniziamo!
Relazione tra lavoro ed energia cinetica
In un certo senso, il lavoro è la quantità di energia messa in un compito (o, forse, “messa nell’oggetto”). Ad esempio, immagina di raccogliere qualche oggetto dal pavimento e sollevarlo a una certa altezza; abbiamo fatto una certa quantità di lavoro su questo oggetto. Se lo lasciamo andare, però, accelera, come se il lavoro che abbiamo fatto nel sollevare l’oggetto si trasformasse in movimento. Attraverso questo esempio, possiamo ricavare una definizione per l’energia cinetica, che è l’energia del movimento. Questa definizione, come vedremo, è strettamente correlata a come abbiamo definito il lavoro.
Per prima cosa, consideriamo un oggetto: una palla di massa m. Raccoglieremo la palla da un tavolo e la solleveremo di una distanza h sopra quel tavolo, come mostrato di seguito. Abbiamo quindi fatto una quantità di lavoro W = mgh, (questo risultato è il prodotto della grandezza del vettore di spostamento (h) e della forza applicata (mg) – i vettori corrispondenti sono paralleli).
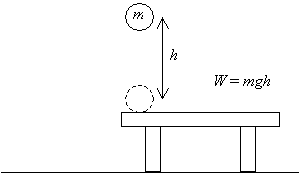
Ora, se rilasciamo quella palla e la lasciamo cadere dall’altezza h sopra il tavolo, una volta che ritorna alla sua altezza originale (il livello del tavolo), avrà una certa velocità v risultante dall’accelerazione dovuta alla gravità.
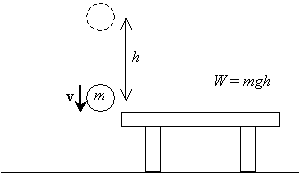
Vogliamo calcolare questa velocità (o velocità, tecnicamente – possiamo occasionalmente sostituire il termine velocità per velocità, ma essere sempre consapevoli che la velocità è in realtà un vettore e la velocità è la grandezza della velocità). Sappiamo che l’accelerazione dovuta alla gravità è costante e che la velocità iniziale della palla è zero (è stazionaria prima che venga rilasciata). Assumeremo che l’altezza iniziale della palla sia h e che la sua altezza finale sia zero (il livello del tavolo). Per calcolare la velocità derivando le formule appropriate, richiediamo l’uso del calcolo integrale elementare. (Se sei uno studente avanzato o stai cercando una sfida extra, puoi provare a derivare queste formule nelle condizioni sopra descritte. Si noti semplicemente che la velocità v della palla è il tasso di tempo di cambiamento della sua posizione x in funzione del tempo t, ![]() , e che l’accelerazione a è il tasso di tempo di cambiamento della velocità,
, e che l’accelerazione a è il tasso di tempo di cambiamento della velocità, ![]() .)
.)
![]()
![]()
Queste formule esprimono la velocità in funzione del tempo, v(t) e la posizione (altezza) in funzione del tempo, x(t), in termini di accelerazione a, altezza h e tempo t. Sappiamo che a = –g, poiché la palla è accelerata solo dalla gravità e questa accelerazione è verso il basso (da qui il segno negativo). La posizione finale della palla è zero metri, o x (t) = 0. Calcoliamo t, la quantità di tempo tra il rilascio della palla e il suo arrivo a livello del tavolo.
![]()
![]()
![]()
Ora, calcoliamo la velocità della palla in questo momento.
![]()
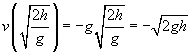
Confrontiamo ora questo risultato con il lavoro originariamente fatto sull’oggetto: W = mgh. Nota quanto sono vicine nella forma queste due espressioni; infatti, l’unico fattore mancante dalla velocità è la massa della palla, m. Se quadrassimo la velocità, moltiplicata per m, e poi divisa per 2, avremmo infatti la stessa espressione del lavoro!
![]()
Quindi, possiamo vedere in un certo senso come può essere derivata la definizione di energia cinetica. L’energia cinetica K di un oggetto, quindi, è uno scalare definito come segue, dove m è la massa dell’oggetto e v è la sua velocità:
![]()
Come risulta, l’energia cinetica è il lavoro svolto su un oggetto dalla forza netta su quell’oggetto. Quindi, sebbene una donna possa fare una certa quantità di lavoro su un oggetto sollevandolo da un’altezza all’altra, la forza netta su quell’oggetto è zero (la donna applica una forza uguale ma opposta nella direzione della gravità). Pertanto, non vi è alcun cambiamento nell’energia cinetica. Se quell’oggetto viene rilasciato e lasciato cadere, tuttavia, guadagna energia cinetica perché la forza netta su di esso è semplicemente quella della gravità (una singola forza). Quindi, per comprendere la relazione tra energia cinetica e lavoro, dobbiamo affinare un po ‘ il nostro concetto di lavoro. Se definiamo il lavoro W come il lavoro totale svolto sull’oggetto da tutte le forze (in altre parole, il lavoro svolto sull’oggetto dalla forza netta), allora vale la seguente relazione tra il lavoro W e le energie cinetiche iniziali e finali (Ki e Kf).
![]() dove
dove ![]()
Quindi, il lavoro netto fatto su un oggetto è uguale alla variazione dell’energia cinetica di quell’oggetto (ΔK). I seguenti problemi di pratica ti offrono l’opportunità di testare e applicare la tua comprensione dei concetti di lavoro ed energia cinetica.
Problema di pratica: Un proiettile di massa 1 chilogrammo viaggia a 5 metri al secondo. Quale velocità deve viaggiare un proiettile da 0,1 chilogrammi per ottenere la stessa energia cinetica?
Soluzione: In primo luogo, calcoliamo l’energia cinetica del proiettile più massiccio (1 chilogrammo).
![]()
Ora possiamo calcolare la velocità dell’oggetto meno massiccio in modo tale che abbia la stessa energia cinetica, K.
![]()
![]()
![]()
Problema di pratica: un uomo solleva un peso di 15 chilogrammi ad un’altezza di due metri da terra prima di farlo cadere. Nell’istante prima che il peso entri in contatto con il terreno, qual è la sua velocità?
Soluzione: Disegniamo un diagramma che illustra le forze che agiscono sull’oggetto mentre viene sollevato e mentre cade; queste forze includono la gravità (Fg) e la forza verso l’alto che l’uomo applica (Fu).
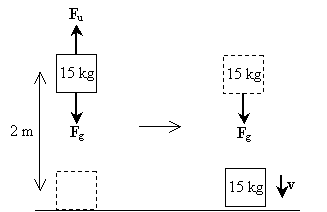
Si noti che la prima fase del processo (sollevamento del peso) non comporta alcuna forza netta che agisce sull’oggetto-la forza dovuta alla gravità è bilanciata dalla forza che l’uomo applica nel sollevamento del peso. Nella seconda fase, tuttavia, il peso sperimenta solo la forza di gravità. La forza netta, in questo caso, è quindi mg nella direzione verso il basso. Come tale, la velocità dell’oggetto è anche nella direzione verso il basso. Il lavoro svolto sul peso a causa della gravità è semplicemente mgh; questo è anche il lavoro totale svolto sul peso durante tutto il processo. Si noti che l’energia cinetica iniziale del peso è zero perché ha velocità zero. Calcoliamo ora la velocità applicando la relazione tra il lavoro in rete e il cambiamento dell’energia cinetica.