Stationarity significa che le proprietà statistiche di una serie temporale cioè media, varianza e covarianza non cambiano nel tempo. Molti modelli statistici richiedono che la serie sia stazionaria per fare previsioni efficaci e precise.
Due test statistici sarebbero utilizzati per verificare la stazionarietà di una serie temporale – Augmented Dickey Fuller (“ADF”) test e Kwiatkowski-Phillips-Schmidt-Shin (“KPSS”) test. Si utilizza anche un metodo per convertire una serie temporale non stazionaria in serie stazionarie.
Questa prima cella importa pacchetti standard e imposta i grafici in linea.
:
%matplotlib inlineimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport statsmodels.api as sm
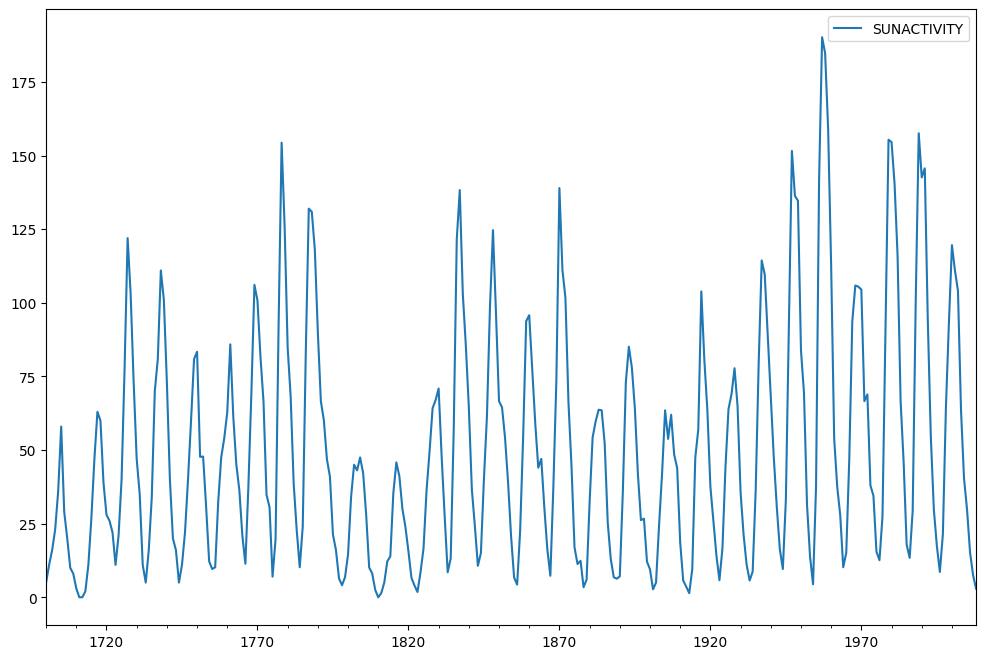
Viene utilizzato il set di dati Sunspots. Contiene dati annuali (1700-2008) sulle macchie solari dal National Geophysical Data Center.
:
sunspots = sm.datasets.sunspots.load_pandas().data
Alcuni pre-elaborazione viene effettuata sui dati. La colonna “ANNO” viene utilizzata nella creazione dell’indice.
:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))del sunspots
I dati sono tracciati ora.
:
sunspots.plot(figsize=(12,8))
:
<AxesSubplot:>
Test ADF¶
Il test ADF viene utilizzato per determinare la presenza di radice unitaria nella serie e quindi aiuta a capire se la serie è stazionaria o meno. Le ipotesi nulle e alternative di questo test sono:
Ipotesi nulla: la serie ha una radice unitaria.
Ipotesi alternativa: la serie non ha radice unitaria.
Se l’ipotesi nulla in non è stata respinta, questo test può fornire la prova che la serie non è stazionaria.
Viene creata una funzione per eseguire il test ADF su una serie temporale.
:
from statsmodels.tsa.stattools import adfullerdef adf_test(timeseries): print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC') dfoutput = pd.Series(dftest, index=) for key,value in dftest.items(): dfoutput = value print (dfoutput)
KPSS test¶
KPSS è un altro test per verificare la stazionarietà di una serie temporale. Le ipotesi nulle e alternative per il test KPSS sono opposte a quelle del test ADF.
Ipotesi nulla: il processo è stazionario.
Ipotesi alternativa: la serie ha una radice unitaria (la serie non è stazionaria).
Viene creata una funzione per eseguire il test KPSS su una serie temporale.
:
from statsmodels.tsa.stattools import kpssdef kpss_test(timeseries): print ('Results of KPSS Test:') kpsstest = kpss(timeseries, regression='c', nlags="auto") kpss_output = pd.Series(kpsstest, index=) for key,value in kpsstest.items(): kpss_output = value print (kpss_output)
I test ADF forniscono i seguenti risultati: statistica del test, valore p e valore critico a intervalli di confidenza di 1%, 5% e 10%.
Il test ADF viene ora applicato sui dati.
:
adf_test(sunspots)
Results of Dickey-Fuller Test:Test Statistic -2.837781p-value 0.053076#Lags Used 8.000000Number of Observations Used 300.000000Critical Value (1%) -3.452337Critical Value (5%) -2.871223Critical Value (10%) -2.571929dtype: float64
in Base al livello di significatività di 0.05 e p-value del test ADF, l’ipotesi nulla non può essere rifiutata. Quindi, la serie non è stazionaria.
I test KPSS forniscono i seguenti risultati: statistica del test, valore p e valore critico a intervalli di confidenza di 1%, 5% e 10%.
Il test KPSS viene ora applicato ai dati.
:
kpss_test(sunspots)
Results of KPSS Test:Test Statistic 0.669866p-value 0.016285Lags Used 7.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
Sulla base del livello di significatività di 0.05 e del valore p del test KPSS, ci sono prove per rifiutare l’ipotesi nulla a favore dell’alternativa. Quindi, la serie non è stazionaria secondo il test KPSS.
È sempre meglio applicare entrambi i test, in modo da poter garantire che la serie sia veramente stazionaria. I possibili risultati dell’applicazione di questi test stazionari sono i seguenti:
Qui, a causa della differenza nei risultati del test ADF e del test KPSS, si può dedurre che la serie è stazionaria e non stazionaria. La serie può essere detrended dalle differenze o dal montaggio del modello.
Detrending by Differencing¶
È uno dei metodi più semplici per detrending di una serie temporale. Viene costruita una nuova serie in cui il valore nella fase temporale corrente viene calcolato come differenza tra l’osservazione originale e l’osservazione nella fase temporale precedente.
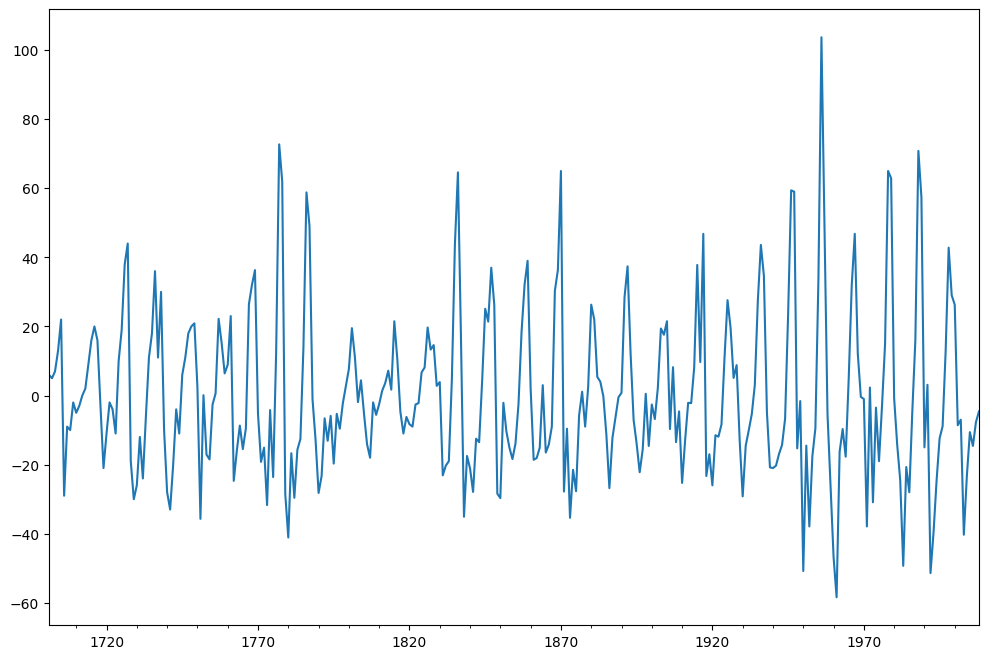
La differenza viene applicata sui dati e il risultato viene tracciato.
:
sunspots = sunspots - sunspots.shift(1)sunspots.dropna().plot(figsize=(12,8))
:
<AxesSubplot:>
Il test ADF viene ora applicato su questi valori detratti e viene verificata la stazionarietà.
:
adf_test(sunspots.dropna())
Results of Dickey-Fuller Test:Test Statistic -1.486166e+01p-value 1.715552e-27#Lags Used 7.000000e+00Number of Observations Used 3.000000e+02Critical Value (1%) -3.452337e+00Critical Value (5%) -2.871223e+00Critical Value (10%) -2.571929e+00dtype: float64
Sulla base del valore p del test ADF, ci sono prove per rifiutare l’ipotesi nulla a favore dell’alternativa. Quindi, la serie è rigida stazionaria ora.
Il test KPSS viene ora applicato su questi valori detratti e viene verificata la stazionarietà.
:
kpss_test(sunspots.dropna())
Results of KPSS Test:Test Statistic 0.021193p-value 0.100000Lags Used 0.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/stattools.py:1911: InterpolationWarning: The test statistic is outside of the range of p-values available in thelook-up table. The actual p-value is greater than the p-value returned. warn_msg.format(direction="greater"), InterpolationWarning
Basato su il p-value del test KPSS, l’ipotesi nulla non può essere rifiutata. Quindi, la serie è stazionaria.
Conclusione¶
Vengono utilizzati due test per verificare la stazionarietà di una serie temporale, ovvero il test ADF e il test KPSS. Il detrimento viene effettuato utilizzando la differenziazione. Le serie temporali stazionarie di tendenza vengono convertite in serie temporali stazionarie rigorose. Il modello di previsione richiesto può ora essere applicato su dati di serie temporali stazionarie.