The Basics: KNN for classification and regression

Data Science from the ground up

I corsi di data science o applied statistics in genere iniziano con modelli lineari, ma a suo modo, K-nearest neighbors è probabilmente il modello più semplice ampiamente utilizzato concettualmente. I modelli KNN sono in realtà solo implementazioni tecniche di un’intuizione comune, che le cose che condividono caratteristiche simili tendono ad essere, beh, simili. Questa non è una visione profonda, tuttavia queste implementazioni pratiche possono essere estremamente potenti e, in modo cruciale per qualcuno che si avvicina a un set di dati sconosciuto, possono gestire le non linearità senza alcuna complicata ingegneria dei dati o configurazione del modello.

Cosa

Come esempio illustrativo, consideriamo il caso più semplice di utilizzare un modello KNN come classificatore. Supponiamo che tu abbia punti dati che rientrano in una delle tre classi. Un esempio bidimensionale può assomigliare a questo:

Probabilmente puoi vedere abbastanza chiaramente che le diverse classi sono raggruppate insieme — l’angolo in alto a sinistra dei grafici sembra appartenere alla classe arancione, la sezione destra/centrale alla classe blu. Se ti venissero date le coordinate del nuovo punto da qualche parte sul grafico e chiedessi a quale classe probabilmente appartenesse, la maggior parte delle volte la risposta sarebbe abbastanza chiara. Qualsiasi punto nell’angolo in alto a sinistra del grafico è probabile che sia arancione, ecc.

Il compito diventa un po ‘ meno sicuro tra le classi, tuttavia, dove dobbiamo stabilirci su un confine decisionale. Considera il nuovo punto aggiunto in rosso qui sotto:

Questo nuovo punto dovrebbe essere classificato come arancione o blu? Il punto sembra cadere tra i due cluster. La tua prima intuizione potrebbe essere quella di scegliere il cluster più vicino al nuovo punto. Questo sarebbe l’approccio del “vicino più vicino”, e nonostante sia concettualmente semplice, produce spesso previsioni piuttosto ragionevoli. Quale punto precedentemente identificato è il nuovo punto più vicino? Potrebbe non essere evidente eyeballing il grafico di quale sia la risposta, ma è facile per il computer per eseguire attraverso i punti e di darci una risposta:

sembra Che il punto più vicino è il blu di categoria, quindi, il nostro nuovo punto probabilmente è troppo. Questo è il metodo più vicino.

A questo punto potresti chiederti a cosa serve la ‘k’ in k-nearest-neighbors. K è il numero di punti vicini che il modello esaminerà quando valuta un nuovo punto. Nel nostro esempio più semplice di nearest neighbor, questo valore per k era semplicemente 1 – abbiamo guardato il vicino più vicino e basta. Si potrebbe, tuttavia, hanno scelto di guardare il più vicino 2 o 3 punti. Perché questo è importante e perché qualcuno dovrebbe impostare k a un numero più alto? Per prima cosa, i confini tra le classi potrebbero urtare uno accanto all’altro in modi che rendono meno ovvio che il punto più vicino ci darà la giusta classificazione. Considera le regioni blu e verdi nel nostro esempio. Infatti, cerchiamo di ingrandire su di loro:

Si noti che mentre le regioni complessive sembrano abbastanza distinte, i loro confini sembrano essere un po ‘ intrecciati tra loro. Questa è una caratteristica comune dei set di dati con un po ‘ di rumore. Quando questo è il caso, diventa più difficile classificare le cose nelle aree di confine. Considerare questo nuovo punto di:

da un lato, visivamente sembra più vicino precedentemente identificati punto è il blu, il nostro computer può facilmente confermare per noi:

D’altra parte, quel punto blu più vicino sembra un po ‘ un outlier, lontano dal centro della regione blu e una sorta di circondato da punti verdi. E questo nuovo punto è anche all’esterno di quel punto blu! E se guardassimo i tre punti più vicini al nuovo punto rosso?

O anche i cinque punti più vicini al nuovo punto?

Ora sembra che il nostro nuovo punto sia in un quartiere verde! È successo di avere un punto blu vicino, ma la preponderanza o punti vicini sono verdi. In questo caso, forse avrebbe senso impostare un valore più alto per k, guardare una manciata di punti vicini e farli votare in qualche modo sulla previsione per il nuovo punto.

Il problema illustrato è eccessivo. Quando k è impostato su uno, il confine tra le regioni identificate dall’algoritmo come blu e verde è irregolare, si snoda indietro con ogni singolo punto. Il punto rosso sembra che potrebbe essere nella regione blu:

Portando k fino a 5, tuttavia, attenua il confine della decisione mentre i diversi punti vicini votano. Il punto rosso ora sembra saldamente nel quartiere verde:

Il compromesso con valori più alti di k è la perdita di granularità nel limite della decisione. L’impostazione di k molto alta tenderà a darti confini lisci, ma i confini del mondo reale che stai cercando di modellare potrebbero non essere perfettamente lisci.

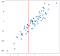
In pratica, possiamo usare lo stesso tipo di approccio dei vicini più vicini per le regressioni, dove vogliamo un valore individuale piuttosto che una classificazione. Considera la seguente regressione di seguito:

I dati sono stati generati casualmente, ma sono stati generati per essere lineari, quindi un modello di regressione lineare si adatterebbe naturalmente bene a questi dati. Voglio sottolineare, tuttavia, che è possibile approssimare i risultati del metodo lineare in un modo concettualmente più semplice con un approccio K-nearest neighbors. La nostra ‘regressione’ in questo caso non sarà una singola formula come ci darebbe un modello OLS, ma piuttosto un valore di output previsto per ogni dato input. Considerare il valore di -.75 sull’asse x, che ho segnato con una linea verticale:

Senza risolvere qualsiasi equazione possiamo arrivare ad una ragionevole approssimazione di ciò che l’uscita dovrebbe essere considerando i punti di interesse:

ha senso che il predetto valore dovrebbe essere vicino a questi punti, non di molto inferiore o superiore. Forse una buona previsione sarebbe la media di questi punti:

Si può immaginare di fare questo per tutti i possibili valori di input e venire con le previsioni ovunque:

il Collegamento di tutte queste previsioni con una linea che ci dà la nostra regressione:

In questo caso, i risultati non sono una linea pulita, ma non traccia la salita dei dati ragionevolmente bene. Questo potrebbe non sembrare terribilmente impressionante, ma uno dei vantaggi della semplicità di questa implementazione è che gestisce bene la non linearità. In considerazione di questa nuova raccolta di punti:

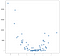
Questi punti sono stati generati semplicemente squadratura i valori dell’esempio precedente, ma supponiamo si è imbattuto in una serie di dati come questo in natura. Ovviamente non è di natura lineare e mentre un modello di stile OLS può facilmente gestire questo tipo di dati, richiede l’uso di termini non lineari o di interazione, il che significa che lo scienziato dei dati deve prendere alcune decisioni su quale tipo di ingegneria dei dati eseguire. L’approccio KNN non richiede ulteriori decisioni: lo stesso codice che ho usato nell’esempio lineare può essere riutilizzato interamente sui nuovi dati per produrre un insieme di previsioni praticabili:

Come per gli esempi di classificatori, l’impostazione di un valore k più alto ci aiuta a evitare l’overfit, anche se potresti iniziare a perdere potenza predittiva sul margine, in particolare intorno ai bordi del tuo set di dati. Considera il primo set di dati di esempio con le previsioni fatte con k impostato su uno, ovvero un approccio più vicino:

Le nostre previsioni saltano in modo irregolare mentre il modello salta da un punto del set di dati a quello successivo. Al contrario, l’impostazione di k a dieci, in modo che dieci punti totali siano mediati insieme per la previsione produce una corsa molto più fluida:

Generalmente sembra migliore, ma puoi vedere qualcosa di un problema ai bordi dei dati. Poiché il nostro modello sta prendendo così tanti punti in considerazione per una data previsione, quando ci avviciniamo a uno dei bordi del nostro campione, le nostre previsioni iniziano a peggiorare. Possiamo affrontare questo problema in qualche modo ponderando le nostre previsioni ai punti più vicini, anche se questo viene fornito con i suoi compromessi.

Come

Quando si imposta un modello KNN ci sono solo una manciata di parametri che devono essere scelti/possono essere modificati per migliorare le prestazioni.

K: il numero di vicini: Come discusso, l’aumento di K tenderà a smussare i confini decisionali, evitando il sovraccarico a costo di una certa risoluzione. Non esiste un singolo valore di k che funzioni per ogni singolo set di dati. Per i modelli di classificazione, specialmente se ci sono solo due classi, di solito viene scelto un numero dispari per k. Questo è così che l’algoritmo non si imbatte mai in un “pareggio”: ad esempio, guarda i quattro punti più vicini e scopre che due di loro sono nella categoria blu e due sono nella categoria rossa.

Distanza metrica: Ci sono, a quanto pare, diversi modi per misurare quanto “vicini” due punti sono l’uno all’altro, e le differenze tra questi metodi possono diventare significative in dimensioni superiori. Il più comunemente usato è la distanza euclidea, l’ordinamento standard che potresti aver imparato nella scuola media usando il teorema di Pitagora. Un’altra metrica è la cosiddetta “Manhattan distance”, che misura la distanza percorsa in ogni direzione cardinale, piuttosto che lungo la diagonale (come se si stesse camminando da un incrocio di strada a Manhattan all’altro e si dovesse seguire la griglia stradale piuttosto che essere in grado di prendere il percorso più breve “in linea d’aria”). Più in generale, queste sono in realtà entrambe le forme di quella che viene chiamata “distanza di Minkowski”, la cui formula è:

Quando p è impostato su 1, questa formula è la stessa della distanza di Manhattan, e quando è impostata su due, la distanza euclidea.

Pesi: un modo per risolvere sia il problema di un possibile “pareggio” quando l’algoritmo vota su una classe sia il problema in cui le nostre previsioni di regressione sono peggiorate verso i bordi del set di dati è introducendo la ponderazione. Con i pesi, i punti vicini conteranno più dei punti più lontani. L’algoritmo sarà ancora guardare tutti i vicini più vicini k, ma i vicini più vicini avranno più di un voto rispetto a quelli più lontani. Questa non è una soluzione perfetta e porta in primo piano la possibilità di overfitting di nuovo. Considera il nostro esempio di regressione, questa volta con i pesi:

Le nostre previsioni vanno direttamente al bordo del set di dati ora, ma puoi vedere che le nostre previsioni ora oscillano molto più vicino ai singoli punti. Il metodo ponderato funziona ragionevolmente bene quando ci si trova tra i punti, ma man mano che ci si avvicina sempre più a un punto particolare, il valore di quel punto ha sempre più un’influenza sulla previsione dell’algoritmo. Se ti avvicini abbastanza a un punto, è quasi come impostare k su uno, dal momento che quel punto ha così tanta influenza.

Ridimensionamento/normalizzazione: un ultimo punto, ma di fondamentale importanza, è che i modelli KNN possono essere eliminati se diverse variabili di funzionalità hanno scale molto diverse. Considera un modello che cerca di prevedere, ad esempio, il prezzo di vendita di una casa sul mercato in base a caratteristiche come il numero di camere da letto e la metratura totale della casa, ecc. C’è più varianza nel numero di piedi quadrati in una casa che c’è nel numero di camere da letto. In genere, le case hanno solo una piccola manciata di camere da letto, e nemmeno la più grande villa avrà decine o centinaia di camere da letto. I piedi quadrati, d’altra parte, sono relativamente piccoli, quindi le case possono variare da vicino a, diciamo, 1,000 sq feat sul lato piccolo a decine di migliaia di piedi quadrati sul lato grande.

Considera il confronto tra una casa di 2.000 piedi quadrati con 2 camere da letto e una casa di 2.010 piedi quadrati con due camere da letto – 10 mq. piedi difficilmente fa la differenza. Al contrario, una casa di 2.000 piedi quadrati con tre camere da letto è molto diversa e rappresenta un layout molto diverso e forse più angusto. Un computer ingenuo non avrebbe il contesto per capirlo, tuttavia. Direbbe che la camera da letto 3 è solo ‘una’ unità di distanza dalla camera da letto 2, mentre il piè di pagina 2,010 sq è ‘dieci’ lontano dal piè di pagina 2,000 sq. Per evitare ciò, è necessario ridimensionare i dati delle funzionalità prima di implementare un modello KNN.

Punti di forza e di debolezza

I modelli KNN sono facili da implementare e gestire bene le non linearità. Anche il montaggio del modello tende ad essere rapido: il computer non deve calcolare parametri o valori particolari, dopotutto. Il compromesso qui è che mentre il modello è veloce da configurare, è più lento da prevedere, poiché per prevedere un risultato per un nuovo valore, sarà necessario cercare tutti i punti nel suo set di allenamento per trovare quelli più vicini. Per i set di dati di grandi dimensioni, KNN può quindi essere un metodo relativamente lento rispetto ad altre regressioni che potrebbero richiedere più tempo per adattarsi, ma poi fare le loro previsioni con calcoli relativamente semplici.

Un altro problema con un modello KNN è che manca di interpretabilità. Una regressione lineare OLS avrà coefficienti chiaramente interpretabili che possono a loro volta dare qualche indicazione della “dimensione dell’effetto” di una determinata caratteristica (anche se, qualche cautela deve essere presa quando si assegna la causalità). Chiedere quali caratteristiche hanno l’effetto più grande non ha senso per un modello KNN, tuttavia. In parte a causa di ciò, anche i modelli KNN non possono essere realmente utilizzati per la selezione delle funzionalità, nel modo in cui può essere una regressione lineare con un termine di funzione di costo aggiunto, come ridge o lazo, o il modo in cui un albero decisionale sceglie implicitamente quali caratteristiche sembrano più preziose.