基本：分類と回帰のためのKNN

ゼロからのデータサイエンス

データサイエンスまたは応用統計コースは、通常、線形モデルから始まりますが、その方法では、k最近傍はおそらく概念的に広く使用されている最も簡単なモデルです。 KNNモデルは、実際には共通の直感の単なる技術的実装であり、同様の機能を共有するものはよく似ている傾向があります。 これはほとんど深い洞察力ではありませんが、これらの実用的な実装は非常に強力であり、未知のデータセットに近づいている人にとっては、複雑なデー

とは

例示的な例として、KNNモデルを分類子として使用する最も単純なケースを考えてみましょう。 たとえば、3つのクラスのいずれかに分類されるデータポイントがあるとします。 二次元の例は次のようになります:

おそらく、異なるクラスが一緒にグループ化されていることをかなり明確に見ることができます—グラフの左上隅はオレンジ色のクラスに属しているように見え、右/中央のセクションは青のクラスに属しています。 グラフ上のどこかに新しい点の座標が与えられ、どのクラスに属する可能性があるかを尋ねられた場合、ほとんどの場合、答えはかなり明確です。 グラフの左上隅の任意の点は、オレンジ色などになる可能性があります。

ただし、決定境界に落ち着く必要があるクラスの間では、タスクは少し確実になりません。 下の赤で追加された新しい点を考えてみましょう:

この新しいポイントはオレンジか青に分類されるべきでしょうか？ ポイントは2つのクラスターの間にあるようです。 あなたの最初の直感は、新しいポイントに近いクラスターを選択することかもしれません。 これは”最近傍”アプローチであり、概念的には単純であるにもかかわらず、かなり賢明な予測が得られることがよくあります。 以前に識別された点は、新しい点に最も近いものですか？ 答えが何であるかをグラフに目を通すだけでは明らかではないかもしれませんが、コンピュータがポイントを実行して答えを与えるのは簡単です:

で囲まれていると、最も近い点が青いカテゴリにあるように見えるので、新しい点もおそらくそうです。 それが最近傍法です。この時点で、k-nearest-neighborsの’k’が何のためのものか疑問に思うかもしれません。 Kは、新しい点を評価するときにモデルが見る近傍点の数です。 最も単純な最近傍の例では、kのこの値は単純に1でした。 あなたは、しかし、最も近い2または3ポイントを見て選択した可能性があります。 なぜこれが重要であり、なぜ誰かがkをより高い数に設定するのでしょうか？ 一つには、クラス間の境界は、最も近い点が私たちに正しい分類を与えることをあまり明白にする方法で互いに隣り合ってぶつかるかもしれません。 この例では、青と緑の領域を考えてみましょう。 実際には、のは、それらにズームインしてみましょう:

全体の領域は十分にはっきりしているように見えますが、境界は少し絡み合っているように見えます。 これは、ノイズのビットを持つデータセットの共通の特徴です。 この場合、境界領域内のものを分類することは困難になります。 この新しい点を考えてみましょう:

一方で、視覚的には、以前に識別された最も近い点が青であるように間違いなく見えます。:

に閉じられます一方、最も近い青い点は、青い領域の中心から遠く離れていて、緑の点で囲まれているように見えます。 そして、この新しいポイントは、その青いポイントの外側にもあります！ 新しい赤い点に最も近い3つの点を見た場合はどうなりますか？

または新しいポイントに最も近い5つのポイントを見ることができますか？

今、私たちの新しいポイントは緑の近所にあるようです！ それは近くの青い点を持っていたが、優勢または近くの点は緑色である。 この場合、kに高い値を設定し、近くの一握りの点を見て、新しい点の予測に何らかの形で投票させることは理にかなっているかもしれません。

説明されている問題は過剰にフィットしています。 Kを1に設定すると、アルゴリズムによって青と緑として識別される領域の境界はでこぼこであり、個々の点ごとに蛇行します。 赤い点は青い領域にあるように見えます:

kを5にすると、異なる近くのポイントが投票するにつれて決定境界が滑らかになります。 赤い点は今、緑の近所にしっかりと見えます:

に基づいて決定が行われるようになりました。kの値が高いとのトレードオフは、決定境界の粒度の損失です。 Kを非常に高く設定すると、境界が滑らかになる傾向がありますが、モデル化しようとしている現実世界の境界は完全に滑らかではない可能性があ

実際には、回帰に同じ種類の最近傍アプローチを使用することができ、分類ではなく個々の値が必要です。 以下の回帰を考えてみましょう:

データはランダムに生成されましたが、線形に生成されたため、線形回帰モデルは自然にこのデータによく適合します。 ただし、K-nearest neighborsアプローチを使用すると、概念的に簡単な方法で線形法の結果を近似できることを指摘したいと思います。 この場合の私たちの「回帰」は、OLSモデルが私たちに与えるような単一の式ではなく、任意の入力に対して最良の予測された出力値になります。 -の値を考えてみましょう。私は垂直線でマークしたx軸上の75:

方程式を解くことなく、近くの点を考慮するだけで、出力がどうあるべきかの合理的な近似に来ることができます:

予測値はこれらのポイントの近くにあり、それほど低くも高くもないことが理にかなっています。 おそらく良い予測は、これらのポイントの平均になります:

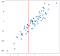
すべての可能な入力値に対してこれを行い、どこでも予測を考え出すことを想像することができます:

これらすべての予測を線で接続すると、回帰が得られます:

この場合、結果はきれいな線ではありませんが、データの上向きの傾きを合理的にトレースします。 これはそれほど印象的ではないように見えるかもしれませんが、この実装の単純さの利点の1つは、非線形性をうまく処理することです。 ポイントのこの新しいコレクションを考えてみましょう:

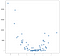
これらの点は、前の例の値を単純に二乗することによって生成されましたが、野生でこのようなデータセットに遭遇したとします。 これは明らかに線形ではなく、OLSスタイルのモデルはこの種のデータを簡単に処理できますが、非線形または相互作用の項を使用する必要があります。 線形の例で使用したのと同じコードを新しいデータで完全に再使用して、実行可能な予測セットを生成することができます:

分類器の例と同様に、値kを高く設定すると、オーバーフィットを回避できますが、マージン、特にデータセットのエッジの周りで予測力が失われる可能性があ Kを1に設定した予測を持つ最初のデータセットの例、つまり最近傍アプローチを考えてみましょう:

モデルがデータセット内のある点から次の点にジャンプするにつれて、予測は不規則にジャンプします。 これとは対照的に、kを10に設定すると、予測のために合計10個のポイントが平均化され、よりスムーズな乗り心地が得られます:

一般的には見栄えが良くなりますが、データの端に問題があります。 私たちのモデルは与えられた予測に対して非常に多くの点を考慮しているので、サンプルのエッジの1つに近づくと、予測は悪化し始めます。 予測をより近い点に重み付けすることで、この問題に多少対処できますが、これには独自のトレードオフがあります。

どのように

KNNモデルを設定するときに選択する必要があるパラメータのほんの一握りがあります/パフォーマンスを向上させるために微調整する

K:近傍の数: 議論されたように、Kを増やすと、決定境界を滑らかにする傾向があり、いくつかの解決を犠牲にして過剰適合を避ける傾向があります。 すべての単一のデータセットで機能する単一の値kはありません。 これは、アルゴリズムが”タイ”に実行されることはありませんので、例えば、最も近い四つの点を見て、それらのうちの二つが青のカテゴリにあり、二つが赤のカテゴリにあることを見つけます。

: 結局のところ、2つの点が互いにどのように「近い」かを測定するさまざまな方法があり、これらの方法の違いは、より高い次元で重要になる可能性が 最も一般的に使用されるのはユークリッド距離で、ピタゴラスの定理を使って中学校で学んだかもしれない標準的な並べ替えです。 別のメトリックは、いわゆる”マンハッタン距離”であり、対角線に沿ってではなく、各基本方向に取られた距離を測定します（マンハッタンのある通りの交差点から別の通りに歩いていたかのように、最短の”カラスが飛ぶように”ルートを取ることができるのではなく、通りのグリッドに従わなければなりませんでした）。 より一般的には、これらは実際には’ミンコフスキー距離’と呼ばれるものの両方の形式であり、その式は次のとおりです:

pが1に設定されている場合、この式はマンハッタン距離と同じであり、twoに設定されている場合、ユークリッド距離です。

Weights:アルゴリズムがクラスに投票するときに可能な”タイ”の問題と、データセットのエッジに向かって回帰予測が悪化する問題の両方を解決する1つの方法は、重み付けを導入することです。 ウェイトを使用すると、近くのポイントは、さらに離れたポイントよりも多くカウントされます。 アルゴリズムはまだすべてのkの最も近い隣人を見ていきますが、近い隣人は遠く離れたものよりも多くの投票を持つことになります。 これは完全な解決ではないし、再度overfittingの可能性を持ち出す。 今回は重みを使って回帰の例を考えてみましょう:

私たちの予測は今データセットの端に右に行きますが、私たちの予測は今、個々のポイントに非常に近 加重法は、ポイントの間にいるときには合理的に機能しますが、特定のポイントに近づくにつれて、そのポイントの値はアルゴリズムの予測にますます影響を与えます。 あなたが点に十分に近づくと、その点には非常に大きな影響があるので、kを1に設定するようなものです。

スケーリング/正規化:最後に、しかし重要な点は、異なる特徴変数が非常に異なるスケールを持つ場合、KNNモデルをスローすることができるということです。 たとえば、寝室の数や家の総面積などの機能に基づいて、市場での家の販売価格を予測しようとするモデルを考えてみましょう。 寝室の数にあるより家の平方フィートの数により多くの分散がある。 典型的には、家にはほんの一握りの寝室しかなく、最大の大邸宅でさえ数十または数百の寝室があるわけではありません。 一方、平方フィートは比較的小さいので、家は小さな側の1,000平方フィートに近いものから大きな側の数万平方フィートまでの範囲である可能性があります。

2,000平方フィートの2ベッドルームの家と2,010平方フィートの2ベッドルームの家—10平方の比較を考えてみましょう。 足はほとんど違いはありません。 対照的に、3つのベッドルームを持つ2,000平方フィートの家は非常に異なっており、非常に異なっており、おそらくより窮屈なレイアウトを表しています。 素朴なコンピュータは、しかし、それを理解するための文脈を持っていないであろう。 3ベッドルームは2ベッドルームから”ワン”ユニットだけであり、2,010sqフッターは2,000sqフッターから”テン”であると言うでしょう。 これを回避するには、KNNモデルを実装する前に機能データをスケーリングする必要があります。

長所と短所

KNNモデルは、実装が容易で、非線形性をうまく処理できます。 結局のところ、コンピュータは特定のパラメータや値を計算する必要はありません。 ここでのトレードオフは、新しい値の結果を予測するためには、トレーニングセット内のすべてのポイントを検索して最も近い値を見つける必要があ したがって、大規模なデータセットの場合、KNNは、近似に時間がかかりますが、比較的簡単な計算で予測を行う他の回帰と比較して、比較的遅い方法にな

KNNモデルのもう1つの問題は、それが解釈可能性を欠いているということです。 OLS線形回帰は、特定の特徴の「効果サイズ」を示すことができる明確に解釈可能な係数を持ちます（ただし、因果関係を割り当てるときは注意が必要です）。 しかし、どの機能が最大の効果を持っているかを尋ねることは、KNNモデルにとっては本当に意味がありません。 このため、KNNモデルは、ridgeやlassoのようなコスト関数項を追加した線形回帰や、決定木が暗黙的にどの特徴が最も価値があるかを選択する方法では、実際には特徴選択に使用することはできません。