運動エネルギーは運動のエネルギーです。 運動エネルギーの表現は、ある相対的な高さに持ち上げられ(したがって、この物体に対して作業が行われる)、落下することが許される物体の場合を見
o運動エネルギー
目的
o仕事の物理学の概念から運動エネルギーの表現を導出する
o仕事と運動エネルギーの関係を理解する
o様々な物体の運動エネルギーを計算する
始めましょう!
仕事と運動エネルギーに関する
ある意味では、仕事はタスクに投入される(または、おそらく”オブジェクトに投入される”)エネルギーの量です。 例えば、我々は床からいくつかのオブジェクトをピックアップし、特定の高さにそれを上げることを想像してみてください; 私たちはそのオブジェクトに対して一定量の作業を行っています。 しかし、それを放すと、物体を持ち上げる作業が動きに変わっているかのように加速します。 この例を通して、我々は運動のエネルギーである運動エネルギーの定義を導出することができます。 この定義は、私たちが見るように、私たちが仕事をどのように定義したかと密接に関連しています。
まず、オブジェクトを考えてみましょう:質量mのボール。 したがって、作業量W=mghを行いました(この結果は、変位ベクトル(h)の大きさと印加された力(mg)の積であり、対応するベクトルは平行です)。
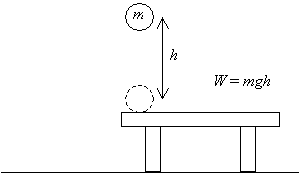
さて、そのボールを離してテーブルの上の高さhから落下させると、元の高さ(テーブルのレベル)に戻ると、重力による加速度に起因する特定の速度vが得ら
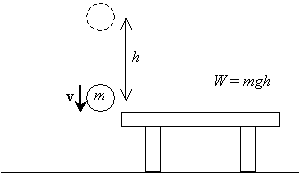
この速度(または速度、技術的には、速度の代わりに速度という用語を使用することがありますが、速度は実際にはベクトルであり、速度は速度の大きさ 重力による加速度は一定であり、ボールの初期速度はゼロであることがわかっています(解放される前は静止しています)。 ボールの最初の高さはhであり、その最終的な高さはゼロ(テーブルのレベル)であると仮定します。 適切な公式を導出することによって速度を計算するために、我々は基本積分計算の使用を必要とする。 (あなたが上級の学生であるか、余分な挑戦を探している場合は、上記の条件の下でこれらの式を自分で導出することを試みることができます。 ボールの速度vは、時間tの関数としての位置xの時間変化率![]() であり、加速度aは速度の時間変化率
であり、加速度aは速度の時間変化率![]() であることに注意してください。)
であることに注意してください。)
![]()
![]()
これらの式は、速度を時間v(t)の関数として、位置(高さ)を時間x(t)の関数として、加速度a、高さh、時間tに関して表現します。 ボールの最終的な位置はゼロメートル、またはx(t)=0です。 ボールがリリースされてからテーブルのレベルに到着するまでの時間であるtを計算しましょう。
![]()
![]()
![]()
さて、この時点でボールの速度を計算しましょう。
![]()
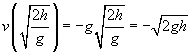
ここで、この結果をオブジェクトで最初に行われた作業と比較してみましょう。W=mgh。 実際には、速度から欠落している唯一の要因は、ボールの質量、mです。mを掛け、速度を二乗し、2で割った場合、実際には仕事と同じ式を持つでしょう!
![]()
したがって、運動エネルギーの定義がどのように導き出すことができるかをある意味で見ることができます。 物体の運動エネルギー Kは、次のように定義されるスカラーであり、mは物体の質量であり、vはその速度である:
![]()
結局のところ、運動エネルギーは、その物体上の正味の力によって物体上で行われる作業である。 したがって、女性はある高さから別の高さに持ち上げることによって物体に対して一定量の作業を行うことができるが、その物体に対する正味の力はゼロである(女性は重力の方向に等しいが反対の力を加える)。 したがって、運動エネルギーに変化はない。 しかし、その物体が解放されて落下することが許されると、その上の正味の力は単に重力の力(単一の力)であるため、運動エネルギーが得られます。 したがって、運動エネルギーと仕事の関係を理解するためには、仕事の概念を幾分洗練しなければなりません。 作業Wをすべての力によって物体上で行われた総作業(つまり、正味の力によって物体上で行われた作業)として定義すると、作業Wと初期および最終運動エネルギー(KiおよびKf)との間の以下の関係が成り立つ。
![]() ここで、
ここで、![]()
したがって、物体に対して行われる正味の仕事は、その物体の運動エネルギー(Δ K)の変化に等しい。 以下の練習問題は、仕事と運動エネルギーの概念の理解をテストして適用する機会を提供します。
練習問題: 質量1キログラムの発射体は毎秒5メートルで移動する。 同じ運動エネルギーを達成するためには、0.1キロの発射体がどのような速度で移動する必要がありますか?
解決策:まず、より巨大な(1キログラム)発射体の運動エネルギーを計算しましょう。
![]()
我々は今、それがこの同じ運動エネルギー、Kを持っているように、あまり大規模なオブジェクトの速度を計算することができます。
![]()
![]()
![]()
練習問題:男はそれをドロップする前に、地面から二メートルの高さに15キロの体重を持ち上げます。 重量が地面と接触する前の瞬間に、その速度は何ですか?
解決策:物体が持ち上げられて落下するときに物体に作用する力を示す図を描きましょう。
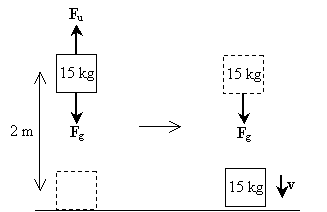
プロセス(重量を持ち上げる)の最初のステップは、物体に作用する正味の力を含まないことに注意してください-重力による力は、人が重量を持ち上げる 第二段階では、しかし、重量は重力の力を経験するだけです。 したがって、この場合の正味の力は、下向きの方向にmgである。 このように、物体の速度も下方方向にある。 重力の結果として重量でできている仕事はmgh単にである;これはまたプロセス中の重量でできている総仕事である。 重量の初期運動エネルギーは、速度がゼロであるためゼロであることに注意してください。 ここで、正味の仕事と運動エネルギーの変化との関係を適用して速度を計算しましょう。