Navigation

反応速度論のモデリング

化学産業におけるプロセス最適化には、考えられる反応系の正確な知識が必要です。 このような知識は、経済性、安全性、効率性などに関する新しいプロセスの開発または既存のプロセスの強化を可能にする。 したがって、プロセスのコア要素としての化学反応器の設計および最適化は特に関心がある。 一般的に、原子炉の設計は、熱力学的および運動論的モデルを含む平衡方程式に基づいている。 速度論的モデルは、システム内の成分の関数として、各反応ステップの反応の過程の数学的記述を構成する。

まず、運動論的モデルの開発には、理想的な実験室規模の反応器での測定が必要です。 実験の総数を合理的に保ち、考慮されたシステムの感度によく適合した実験を実行するために、測定は”実験の計画”（DoE）の統計的方法を介して編成され 収集されたデータを基礎として、定性的に類似したデータポイントを持つ（異なる詳細レベルの）機械論的仮定に依存する適切な運動論的アプローチが、運動論的モデリングのために選択される。 状態変数のほかに（例えば 速度論的アプローチは、測定値（例えば、活性化エネルギー、前指数因子）に数学的アプローチの結果を適応させるために変化させることができるフィッティングパラメータを含む。 各反応ステップに最も適した信頼性の高い速度論的アプローチを特定するために、フィッティング結果は、統計分析（信頼区間、相関係数、残差など）によ). したがって、速度論的モデリングの最終結果は、反応ネットワークの各反応ステップを記述するための完全パラメータ化されたモデルである。 化学反応工学の協会は運動測定および運動模倣を行うために可能性を提供する。 これのために、異なった変数が変わるようにし、組み立てがさまざまな条件にカスタマイズ可能である複数の連続的な、バッチ実験室のスケールリア キネティックモデリングのために、多様な最先端のソフトウェアツール（例えば、Presto Kinetics、Aspen Custom Modeler、Comsol Multiphyics）が使用されている。

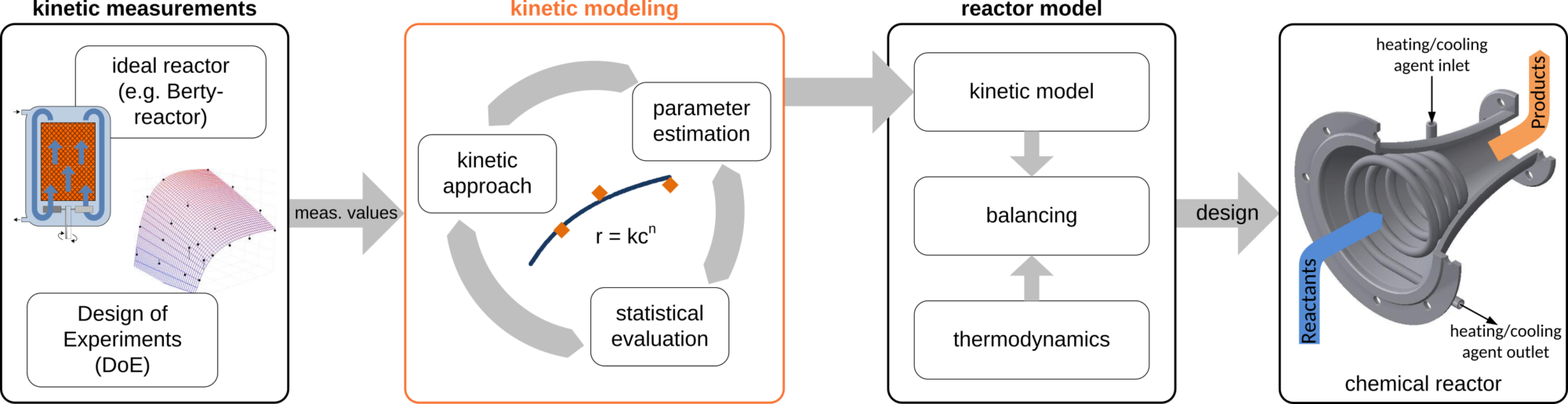
図1.1.1. 1:化学反応器設計の一部としての速度論的モデリング。

例:

反応物Aは、二つの中間生成物BとCを介して最終生成物Dに反応する。:

図1.1.1. 図2:線状反応ネットワーク(左)、分岐反応ネットワーク(右))

図2から分岐した例では、運動論的モデルを含む微分方程式のセットは、次のように書くことができます:

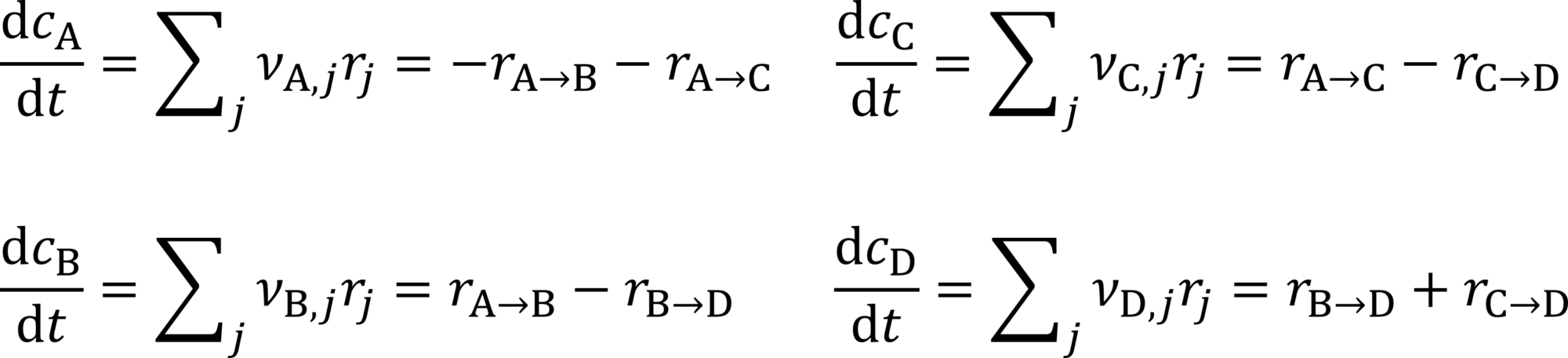
図1.1.1. 3:運動モデル

先に説明したように、適切な速度論的アプローチは、各反応ステップについて同定されなければならない。 べき乗則のアプローチはよく知られており、簡単です。 それらは、それぞれ温度依存速度定数k（T）および成分濃度または分圧によって反応の過程を特徴付ける。 利用可能な多数の運動学的アプローチがあり、そのうちの最も一般的なものは図4に示されています。

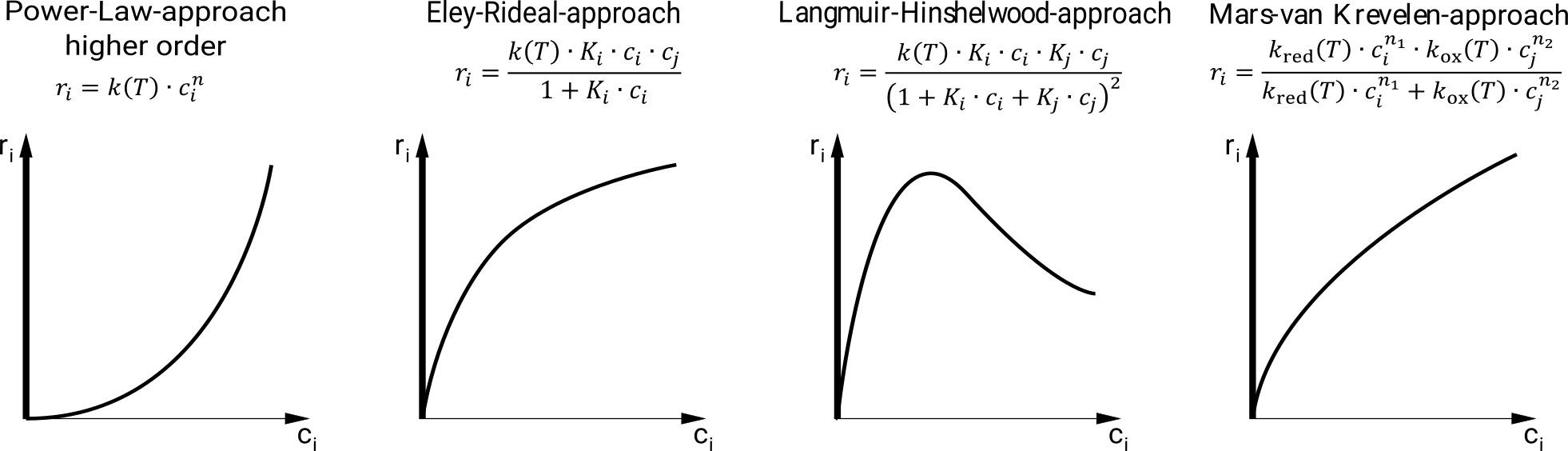
図1.1.1. 4：運動論的表現のための例

通常、速度定数k(T)はアレニウス式を使用して計算されます:

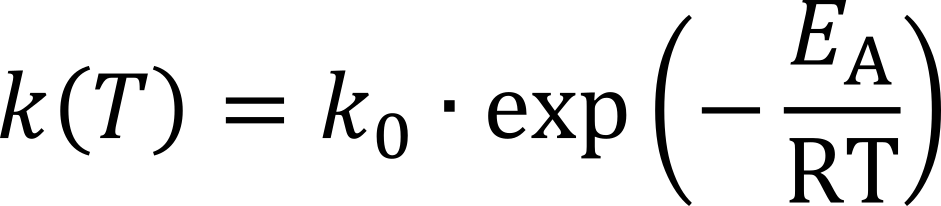
ここで、Ｅ ａおよびｋ０は、活性化エネルギーおよび反応の頻度係数を表す。

資金調達と協力

クラスター-オブ-エクセレンス”先端材料工学”（EAM）

業界パートナー

最新の出版物