the Basics: KNN voor classificatie en regressie

Data Science from the ground up

Data science of applied statistics cursussen beginnen meestal met lineaire modellen, maar op zijn manier is K-nearest neighbourhood waarschijnlijk het eenvoudigste veelgebruikte model conceptueel. KNN-modellen zijn eigenlijk gewoon technische implementaties van een gemeenschappelijke intuïtie, dat dingen die vergelijkbare functies hebben de neiging hebben om, nou ja, vergelijkbaar te zijn. Dit is nauwelijks een diep inzicht, maar deze praktische implementaties kunnen extreem krachtig zijn, en, cruciaal voor iemand die een onbekende dataset benadert, kunnen omgaan met niet-lineariteiten zonder ingewikkelde data-engineering of modelopstelling.

wat

als een illustratief voorbeeld, laten we eens kijken naar het eenvoudigste geval van het gebruik van een KNN-model als classifier. Laten we zeggen dat je datapunten hebt die in een van de drie klassen vallen. Een tweedimensionaal voorbeeld kan er zo uitzien:

u kunt waarschijnlijk vrij duidelijk zien dat de verschillende klassen zijn gegroepeerd — de linkerbovenhoek van de grafieken lijkt te behoren tot de oranje klasse, de rechter/middelste sectie naar de blauwe klasse. Als je de coördinaten van het nieuwe punt ergens op de grafiek zou krijgen en gevraagd zou worden tot welke klasse het waarschijnlijk zou behoren, dan zou het antwoord meestal vrij duidelijk zijn. Elk punt in de linkerbovenhoek van de grafiek is waarschijnlijk oranje, enz.

de taak wordt iets minder zeker tussen de klassen, echter, waar we ons moeten vestigen op een beslissingsgrens. Overweeg het nieuwe punt toegevoegd in het rood hieronder:

moet dit nieuwe punt als oranje of blauw worden ingedeeld? Het punt lijkt te vallen tussen de twee clusters. Je eerste intuïtie zou kunnen zijn om de cluster te kiezen die dichter bij het nieuwe punt staat. Dit zou de ‘dichtstbijzijnde buur’ benadering zijn, en ondanks het feit dat het conceptueel eenvoudig is, levert het vaak redelijk verstandige voorspellingen op. Welk eerder geïdentificeerd punt is het nieuwe punt het dichtst bij? Het is misschien niet voor de hand liggend om naar de grafiek te kijken wat het antwoord is, maar het is gemakkelijk voor de computer om door de punten te lopen en ons een antwoord te geven:

lijkt het erop dat het dichtstbijzijnde punt in de blauwe Categorie ligt, dus ons nieuwe punt waarschijnlijk ook. Dat is de methode van de naaste buren.

op dit moment vraagt u zich misschien af waar de ‘k’ in k-dichtstbijzijnde-buren voor is. K is het aantal nabijgelegen punten waar het model naar zal kijken bij het evalueren van een nieuw punt. In ons eenvoudigste voorbeeld van de naaste buurman was deze waarde voor k gewoon 1-We keken naar de dichtstbijzijnde buurman en dat was het. Je had er echter voor kunnen kiezen om naar de dichtstbijzijnde 2 of 3 punten te kijken. Waarom is dit belangrijk en waarom zou iemand k op een hoger getal zetten? Ten eerste kunnen de grenzen tussen klassen naast elkaar botsen op manieren die het minder duidelijk maken dat het dichtstbijzijnde punt ons de juiste classificatie geeft. Denk aan de blauwe en groene gebieden in ons voorbeeld. In feite, laten we inzoomen op hen:

merk op dat hoewel de totale regio’ s duidelijk genoeg lijken, hun grenzen een beetje met elkaar verweven lijken te zijn. Dit is een gemeenschappelijk kenmerk van datasets met een beetje ruis. Wanneer dit het geval is, wordt het moeilijker om dingen in de grensgebieden te classificeren. Overweeg dit nieuwe punt:

enerzijds, visueel lijkt het zeker dat het dichtstbijzijnde eerder geïdentificeerde punt blauw is, wat onze computer gemakkelijk voor ons kan bevestigen:

aan de andere kant lijkt dat dichtstbijzijnde blauwe punt een beetje een uitschieter zelf, ver weg van het centrum van het blauwe gebied en een beetje omgeven door groene punten. En dit nieuwe punt is zelfs aan de buitenkant van dat blauwe punt! Wat als we naar de drie punten kijken die het dichtst bij het nieuwe rode punt liggen?

of zelfs de vijf punten die het dichtst bij het nieuwe punt liggen?

nu lijkt het erop dat ons nieuwe punt zich in een groene buurt bevindt! Het had een nabijgelegen blauwe punt, maar het overwicht of nabijgelegen punten zijn groen. In dit geval zou het misschien zinvol zijn om een hogere waarde voor k in te stellen, om te kijken naar een handvol nabijgelegen punten en hen op de een of andere manier te laten stemmen op de voorspelling voor het nieuwe punt.

het geïllustreerde nummer is te toepasselijk. Wanneer k is ingesteld op een, de grens tussen welke gebieden worden geïdentificeerd door het algoritme als blauw en groen is hobbelig, het slingert terug met elk individueel punt. Het rode punt lijkt in het blauwe gebied te liggen.:

waardoor k op 5 komt, maakt de beslissingsgrens echter glad naarmate de verschillende nabijgelegen punten stemmen. Het rode punt lijkt nu stevig in de groene buurt:

de afweging met hogere waarden van k is het verlies van granulariteit in de beslissingsgrens. Het instellen van k zeer hoog zal de neiging hebben om je gladde grenzen te geven, maar de echte wereld grenzen die je probeert te modelleren zijn misschien niet perfect glad.

praktisch gesproken kunnen we dezelfde benadering van dichtsbijzijnde buren gebruiken voor regressies, waarbij we een individuele waarde willen in plaats van een classificatie. Overweeg de volgende regressie hieronder:

de gegevens werden willekeurig gegenereerd, maar werden gegenereerd om lineair te zijn, dus een lineair regressiemodel paste natuurlijk goed bij deze gegevens. Ik wil er echter op wijzen dat je de resultaten van de lineaire methode conceptueel eenvoudiger kunt benaderen met een K-benadering van de dichtstbijzijnde buren. Onze ‘regressie’ zal in dit geval geen enkele formule zijn zoals een OLS-model Ons zou geven, maar eerder een best voorspelde outputwaarde voor elke gegeven input. Denk aan de waarde van…75 (op de x-as, die ik heb aangegeven met een verticale lijn:

Zonder het oplossen van eventuele vergelijkingen kunnen we komen tot een redelijke benadering van wat de output moet gewoon door te kijken naar de nabijgelegen punten:

Het is logisch dat de voorspelde waarde moet worden in de buurt van deze punten, niet veel lager of hoger zijn. Misschien zou een goede voorspelling Het gemiddelde van deze punten zijn:

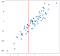
je kunt Je voorstellen dit te doen voor alle mogelijke invoerwaarden en komen met de voorspellingen overal:

het Verbinden van al deze voorspellingen met een lijn geeft ons een regressie:

In dit geval worden de resultaten zijn niet een schone lijn, maar ze doen het traceren van de opwaartse helling van de gegevens redelijk goed. Dit lijkt misschien niet erg indrukwekkend, maar een voordeel van de eenvoud van deze implementatie is dat het goed omgaat met non-lineariteit. Overweeg deze nieuwe verzameling punten:

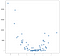
deze punten werden gegenereerd door simpelweg de waarden van het vorige voorbeeld te kwadrateren, maar stel dat je in het wild een dataset als deze tegenkomt. Het is duidelijk niet lineair van aard en hoewel een OLS-stijlmodel dit soort gegevens gemakkelijk kan verwerken, vereist het gebruik van niet-lineaire of interactietermen, wat betekent dat de data scientist een aantal beslissingen moet nemen over wat voor soort Data-engineering moet worden uitgevoerd. De KNN-aanpak vereist geen verdere beslissingen – dezelfde code die ik gebruikte op het lineaire voorbeeld kan volledig worden hergebruikt op de nieuwe gegevens om een werkbare reeks voorspellingen op te leveren:

net als bij de classificatievoorbeelden, helpt het instellen van een hogere waarde k ons om overdaad te voorkomen, hoewel u de voorspellende kracht op de marge kunt verliezen, met name rond de randen van uw dataset. Neem de eerste voorbeeld dataset met voorspellingen gemaakt met k ingesteld op één, dat is een benadering van de naaste buur:

onze voorspellingen springen grillig rond als het model van het ene punt in de dataset naar het volgende springt. Het instellen van k op tien, zodat tien totaalpunten samen gemiddeld worden voor voorspelling, levert daarentegen een veel soepelere rit op:

over het algemeen ziet dat er beter uit, maar je kunt iets van een probleem zien aan de randen van de gegevens. Omdat ons model zoveel punten in aanmerking neemt voor een bepaalde voorspelling, wanneer we dichter bij een van de randen van ons monster komen, beginnen onze voorspellingen slechter te worden. We kunnen deze kwestie enigszins aan te pakken door weging onze voorspellingen naar de dichter punten, hoewel dit komt met zijn eigen afwegingen.

hoe

bij het opzetten van een KNN-model zijn er slechts een handvol parameters die moeten worden gekozen/kunnen worden aangepast om de prestaties te verbeteren.

K: het aantal buren: Zoals besproken, zal het verhogen van K de neiging hebben om beslissingsgrenzen glad te strijken, waarbij overit ten koste van een oplossing wordt vermeden. Er is geen enkele waarde van k die voor elke afzonderlijke dataset zal werken. Voor classificatiemodellen, vooral als er maar twee klassen zijn, wordt meestal een oneven getal gekozen voor k. Dit is zodat het algoritme nooit in een ‘gelijkspel’ terechtkomt: het kijkt bijvoorbeeld naar de dichtstbijzijnde vier punten en vindt dat twee van hen in de blauwe categorie en twee in de rode categorie zitten.

Afstandsmetrisch: Er zijn, zo blijkt, verschillende manieren om te meten hoe ‘dicht’ twee punten zijn aan elkaar, en de verschillen tussen deze methoden kunnen significant worden in hogere dimensies. Het meest gebruikt is Euclidische afstand, de standaard soort die je misschien hebt geleerd op de middelbare school met behulp van de stelling van Pythagoras. Een andere maatstaf is de zogenaamde’ Manhattan distance’, die de afstand meet die in elke kardinale richting wordt genomen, in plaats van langs de diagonaal (alsof je van de ene straat kruising in Manhattan naar de andere loopt en het straatnet moet volgen in plaats van de kortste ‘hemelsbreed’ route te kunnen nemen). Meer in het algemeen, dit zijn eigenlijk beide vormen van wat wordt genoemd ‘Minkowski afstand’, waarvan de formule is:

wanneer p is ingesteld op 1, is deze formule hetzelfde als Manhattan afstand, en wanneer ingesteld op twee, Euclidische afstand.

gewichten: een manier om zowel het probleem van een mogelijke ‘gelijkspel’ op te lossen wanneer het algoritme op een klasse stemt als het probleem waar onze regressievoorspellingen slechter werden naar de randen van de dataset is door weging te introduceren. Bij gewichten tellen de nabije punten meer dan de punten verder weg. Het algoritme zal nog steeds kijken naar alle k dichtstbijzijnde buren, maar de naaste buren zullen meer van een stem dan die verder weg. Dit is geen perfecte oplossing en brengt de mogelijkheid van overbevissing weer. Bekijk ons regressie voorbeeld, dit keer met gewichten:

onze voorspellingen gaan nu tot aan de rand van de dataset, maar je kunt zien dat onze voorspellingen nu veel dichter bij de individuele punten schommelen. De gewogen methode werkt redelijk goed als je tussen punten, maar als je dichter en dichter bij een bepaald punt, dat punt waarde heeft meer en meer van invloed op de voorspelling van het algoritme. Als je dicht genoeg bij een punt komt, is het bijna alsof je k op één zet, omdat dat punt zoveel invloed heeft.

schalen / normaliseren: een laatste, maar cruciaal belangrijk punt is dat KNN-modellen kunnen worden afgeworpen als verschillende feature-variabelen zeer verschillende schalen hebben. Overweeg een model dat probeert te voorspellen, laten we zeggen, de verkoopprijs van een huis op de markt op basis van functies zoals het aantal slaapkamers en de totale vierkante meter van het huis, enz. Er is meer variatie in het aantal vierkante meter in een huis dan in het aantal slaapkamers. Typisch, huizen hebben slechts een klein handvol slaapkamers, en zelfs niet het grootste herenhuis zal tientallen of honderden slaapkamers hebben. Vierkante voet, aan de andere kant, zijn relatief klein, dus huizen kunnen variëren van dicht bij, laten we zeggen, 1.000 vierkante voet aan de kleine kant tot tienduizenden vierkante voet aan de grote kant.

overweeg de vergelijking tussen een huis van 2.000 m2 met 2 slaapkamers en een huis van 2010 m2 met 2 slaapkamers — 10 m2. voeten maken nauwelijks een verschil. Daarentegen, een 2.000 vierkante meter huis met drie slaapkamers is heel anders, en vertegenwoordigt een heel andere en mogelijk meer krappe lay-out. Een naïeve computer zou echter niet de context hebben om dat te begrijpen. Het zou zeggen dat de 3 slaapkamer is slechts’ een ‘ eenheid verwijderd van de 2 slaapkamer, terwijl de 2010 sq footer is ’tien’ afstand van de 2.000 sq footer. Om dit te voorkomen, moeten featuregegevens worden geschaald voordat een KNN-model wordt geïmplementeerd.

sterke en zwakke punten

KNN-modellen zijn gemakkelijk te implementeren en goed om te gaan met niet-lineariteiten. Het aanpassen van het model gaat ook snel: de computer hoeft immers geen bepaalde parameters of waarden te berekenen. De trade off hier is dat terwijl het model is snel op te zetten, het is langzamer te voorspellen, omdat om een uitkomst te voorspellen voor een nieuwe waarde, het zal moeten zoeken door alle punten in de training set om de dichtstbijzijnde te vinden. Voor grote datasets kan KNN daarom een relatief langzame methode zijn in vergelijking met andere regressies die langer kunnen duren om te passen, maar dan hun voorspellingen doen met relatief eenvoudige berekeningen.

een ander probleem met een KNN-model is dat het niet interpreteerbaar is. Een lineaire OLS-regressie zal duidelijk interpreteerbare coëfficiënten hebben die zelf enige indicatie kunnen geven van de’ effectgrootte ‘ van een bepaald kenmerk (hoewel enige voorzichtigheid moet worden betracht bij het toewijzen van causaliteit). Vragen welke functies het grootste effect hebben heeft echter geen zin voor een KNN-model. Mede hierdoor kunnen KNN-modellen ook niet echt worden gebruikt voor functieselectie, zoals een lineaire regressie met een extra kostenfunctieterm, zoals ridge of lasso, kan zijn, of de manier waarop een beslissingsboom impliciet kiest welke functies het meest waardevol lijken.