kinetische energie is de energie van beweging. Een uitdrukking voor kinetische energie wordt afgeleid door te kijken naar het geval van een object dat wordt opgetild tot een relatieve hoogte (dus wordt er aan dit object gewerkt) en dan mag vallen.
sleuteltermen
O kinetische energie
doelstellingen
O Een uitdrukking voor kinetische energie afleiden uit het natuurkundig werkconcept
o de relatie tussen werk en kinetische energie
begrijpen o de kinetische energie van verschillende objecten berekenen
laten we beginnen!
gerelateerd aan werk en kinetische energie
in zekere zin is werk de hoeveelheid energie die in een taak wordt gestoken (of, misschien, “in het object”). Stel je bijvoorbeeld voor dat we een voorwerp van de vloer oppakken en het tot een bepaalde hoogte tillen; we hebben een bepaalde hoeveelheid werk aan dat object gedaan. Als we het echter loslaten, versnelt het, alsof het werk dat we deden bij het optillen van het object in beweging wordt omgezet. Aan de hand van dit voorbeeld kunnen we een definitie afleiden voor kinetische energie, wat bewegingsenergie is. Zoals we zullen zien, hangt deze definitie nauw samen met de manier waarop we het werk hebben gedefinieerd.
laten we eerst een object bekijken: een bal met massa m. we pakken de bal van een tafel en verhogen hem een afstand h boven die tafel, zoals hieronder getoond. We hebben daarom een hoeveelheid werk gedaan W = mgh, (dit resultaat is het product van de grootte van de verplaatsingsvector (h) en de toegepaste kracht (mg) – de overeenkomstige vectoren zijn parallel).
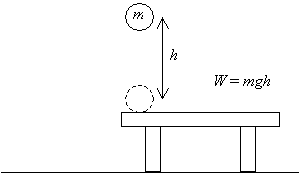
nu, als we die bal loslaten en laten vallen van de hoogte h boven de tafel, zodra hij terugkeert naar zijn oorspronkelijke hoogte (het niveau van de tabel), zal het een bepaalde snelheid v als gevolg van de versnelling als gevolg van de zwaartekracht.
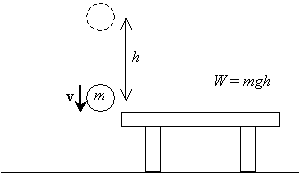
we willen deze snelheid berekenen (of snelheid, technisch gezien-we kunnen af en toe de term snelheid vervangen door snelheid, maar wees je er altijd van bewust dat snelheid eigenlijk een vector is en snelheid de grootte van de snelheid is). We weten dat de versnelling als gevolg van de zwaartekracht constant is en dat de beginsnelheid van de bal nul is (hij staat stil voordat hij wordt losgelaten). We gaan ervan uit dat de initiële hoogte van de bal h is en dat de uiteindelijke hoogte nul is (het niveau van de tabel). Om de snelheid te berekenen door de juiste formules af te leiden, hebben we het gebruik van elementaire integraal calculus nodig. (Als je een gevorderde student bent of op zoek bent naar een extra uitdaging, kun je proberen deze formules onder de bovenstaande voorwaarden zelf af te leiden. Merk gewoon op dat de snelheid v van de bal de tijdssnelheid van zijn positie x is als functie van tijd t, ![]() , en dat de versnelling a de tijdssnelheid van de snelheid,
, en dat de versnelling a de tijdssnelheid van de snelheid, ![]() is.)
is.)
![]()
![]()
deze formules drukken de snelheid uit als functie van de tijd, v(t), en de positie (hoogte) als functie van de tijd, x(t), in termen van de versnelling a, hoogte h, en tijd t. we weten dat a = –g, omdat de bal alleen wordt versneld door de zwaartekracht en deze versnelling naar beneden is (vandaar het negatieve teken). De uiteindelijke positie van de bal is nul meter, of x (t) = 0. Laten we berekenen t, de hoeveelheid tijd tussen de vrijlating van de bal en de aankomst op het niveau van de tafel.
![]()
![]()
![]()
laten we nu de snelheid van de bal berekenen op dit moment.
![]()
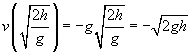
laten we nu dit resultaat vergelijken met het werk dat oorspronkelijk gedaan is op het object: W = mgh. Merk op hoe dicht in vorm deze twee uitdrukkingen zijn; in feite, de enige factor die ontbreekt aan de snelheid is de massa van de bal, m. als we de snelheid kwadraat, vermenigvuldigd met m, en dan gedeeld door 2, zouden we in feite dezelfde uitdrukking hebben als het werk!
![]()
zo kunnen we in zekere zin zien hoe de definitie van kinetische energie kan worden afgeleid. De kinetische energie K van een object is dan een scalair gedefinieerd als volgt, waarbij m de massa van het object is en v De snelheid is:
![]()
het blijkt dat de kinetische energie het werk is van een object door de netto kracht op dat object. Dus, hoewel een vrouw een bepaalde hoeveelheid werk aan een object kan doen door het van de ene hoogte naar de andere te tillen, is de netto kracht op dat object nul (de vrouw past een kracht toe die gelijk is aan maar tegengesteld is in de richting van de zwaartekracht). Er is dus geen verandering in kinetische energie. Als dat object echter wordt vrijgegeven en mag vallen, krijgt het kinetische energie omdat de netto kracht op het is gewoon die van de zwaartekracht (een enkele kracht). Dus, om de relatie tussen kinetische energie en werk te begrijpen, moeten we ons concept van werk enigszins verfijnen. Als we het werk W definiëren als het totale werk dat door alle krachten aan het object wordt gedaan (met andere woorden, het werk dat door de nettokracht aan het object wordt gedaan), dan geldt de volgende relatie tussen het werk W en de initiële en uiteindelijke kinetische energieën (Ki en Kf).
![]() waarbij
waarbij ![]()
het netwerk dat aan een object wordt verricht, is dus gelijk aan de verandering in de kinetische energie van dat object (ΔK). De volgende oefenproblemen bieden u de mogelijkheid om uw begrip van de begrippen werk en kinetische energie te testen en toe te passen.
Praktijkprobleem: Een projectiel met een massa van 1 kilogram reist met 5 meter per seconde. Welke snelheid moet een 0.1-kilogram projectiel afleggen om dezelfde kinetische energie te bereiken?
oplossing: laten we eerst de kinetische energie van het Massievere projectiel (1 kilogram) berekenen.
![]()
We kunnen nu berekenen van de snelheid van de minder massief object, zodanig dat het dezelfde kinetische energie, K.
![]()
![]()
![]()
de Praktijk Probleem: Een man tilt een 15-kilo gewicht tot een hoogte van twee meter boven de grond, voordat ze het. Op het moment dat het gewicht contact maakt met de grond, wat is zijn snelheid?
oplossing: laten we een diagram tekenen dat de krachten illustreert die op het object werken terwijl het wordt opgetild en valt; deze krachten omvatten de zwaartekracht (FG) en de opwaartse kracht die de mens uitoefent (Fu).
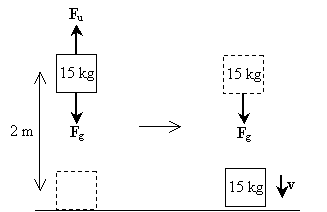
merk op dat de eerste stap van het proces (het heffen van het gewicht) geen netto kracht die op het object-de kracht als gevolg van de zwaartekracht wordt in evenwicht gebracht door de kracht die de mens toepast bij het heffen van het gewicht. In de tweede stap ervaart het gewicht echter alleen de zwaartekracht. De netto kracht, in dit geval, is dus mg in de neerwaartse richting. Als zodanig is de snelheid van het object ook in de neerwaartse richting. Het werk aan het gewicht als gevolg van de zwaartekracht is gewoon mgh; dit is ook het totale werk aan het gewicht gedurende het proces. Merk op dat de initiële kinetische energie van het gewicht nul is omdat het geen snelheid heeft. Laten we nu de snelheid berekenen door de relatie tussen net werk en de verandering in kinetische energie toe te passen.