Estacionaridade significa que as propriedades estatísticas de uma série de tempo, i.e. média, a variância e a covariância não mudam ao longo do tempo. Muitos modelos estatísticos exigem que a série seja estacionária para fazer previsões eficazes e precisas.
dois testes estatísticos seriam usados para verificar a estacionariedade de um teste Dickey Fuller (“ADF”) aumentado em série temporal e teste Kwiatkowski – Phillips-Schmidt-Shin (“KPSS”). Deve igualmente ser utilizado um método para converter uma série temporal não estacionária em série estacionária.
esta primeira célula importa pacotes padrão e define gráficos para aparecer inline.
:
%matplotlib inlineimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport statsmodels.api as sm
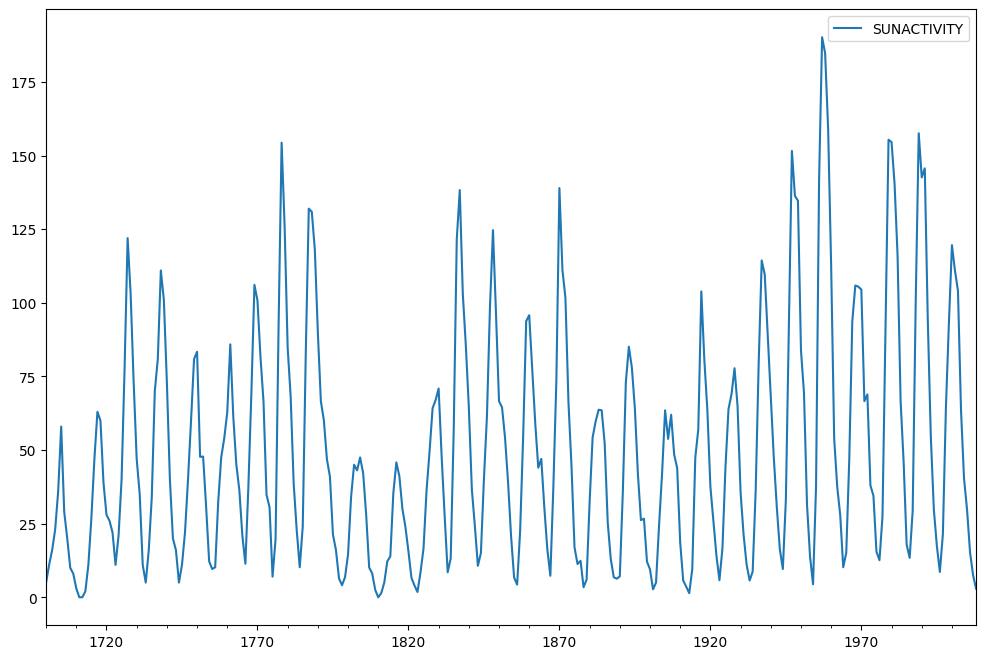
as manchas solares conjunto de dados é usado. Ele contém dados anuais (1700-2008) sobre manchas solares do Data Center Geofísico Nacional.
:
sunspots = sm.datasets.sunspots.load_pandas().data
Alguns pré-processamento é realizado sobre os dados. A coluna ” ano ” é usada na criação de índice.
:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))del sunspots
Os dados são plotados agora.
:
sunspots.plot(figsize=(12,8))
:
<AxesSubplot:>
teste adf¶
o teste ADF é usado para determinar a presença de raiz unitária na série e, portanto, ajuda a entender se a série está estacionária ou não. A hipótese nula e alternativa deste teste são:
hipótese nula: a série tem uma raiz unitária.Hipótese alternativa: a série não tem raiz unitária.
se a hipótese nula não foi rejeitada, este teste pode fornecer evidências de que a série não é estacionária.
uma função é criada para realizar o teste ADF em uma série temporal.
:
from statsmodels.tsa.stattools import adfullerdef adf_test(timeseries): print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC') dfoutput = pd.Series(dftest, index=) for key,value in dftest.items(): dfoutput = value print (dfoutput)
teste KPSS¶
KPSS é outro teste para verificar a estacionaridade de uma série de tempo. A hipótese nula e alternativa para o teste KPSS é oposta à do teste ADF.Hipótese nula: o processo é tendência estacionária.Hipótese alternativa: a série tem uma raiz unitária (a série não é estacionária).
uma função é criada para realizar o teste KPSS em uma série temporal.
:
from statsmodels.tsa.stattools import kpssdef kpss_test(timeseries): print ('Results of KPSS Test:') kpsstest = kpss(timeseries, regression='c', nlags="auto") kpss_output = pd.Series(kpsstest, index=) for key,value in kpsstest.items(): kpss_output = value print (kpss_output)
Os testes ADF dá os seguintes resultados – estatística de teste, valor de p e o valor crítico a 1%, 5% e 10% de intervalos de confiança.
o teste ADF agora é aplicado nos dados.
:
adf_test(sunspots)
Results of Dickey-Fuller Test:Test Statistic -2.837781p-value 0.053076#Lags Used 8.000000Number of Observations Used 300.000000Critical Value (1%) -3.452337Critical Value (5%) -2.871223Critical Value (10%) -2.571929dtype: float64
Baseada no nível de significância de 0,05 e p-valor do teste de ADF, a hipótese nula não pode ser rejeitada. Portanto, a série não é estacionária.
os testes KPSS fornecem os seguintes resultados-estatística de teste, valor p e o valor crítico em intervalos de confiança de 1%, 5% e 10%.
o teste KPSS agora é aplicado nos dados.
:
kpss_test(sunspots)
Results of KPSS Test:Test Statistic 0.669866p-value 0.016285Lags Used 7.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
Baseada no nível de significância de 0,05 e p-valor do teste KPSS, há evidências para rejeitar a hipótese nula em favor da alternativa. Portanto, a série não é estacionária de acordo com o teste KPSS.
é sempre melhor aplicar ambos os testes, para que possa ser assegurado que a série seja verdadeiramente estacionária. Os possíveis resultados da aplicação desses testes estacionários são os seguintes:
aqui, devido à diferença nos resultados do teste ADF e do teste KPSS, pode-se inferir que a série é estacionária de tendência e não estacionária estrita. A série pode ser detrended diferenciando ou pelo encaixe modelo.
Detrending por Differencing¶
é um dos métodos mais simples para detrending uma série temporal. Uma nova série é construída onde o valor na etapa de tempo atual é calculado como a diferença entre a observação original e a observação na etapa de tempo anterior.
a diferenciação é aplicada nos dados e o resultado é plotado.
:
sunspots = sunspots - sunspots.shift(1)sunspots.dropna().plot(figsize=(12,8))
:
<AxesSubplot:>
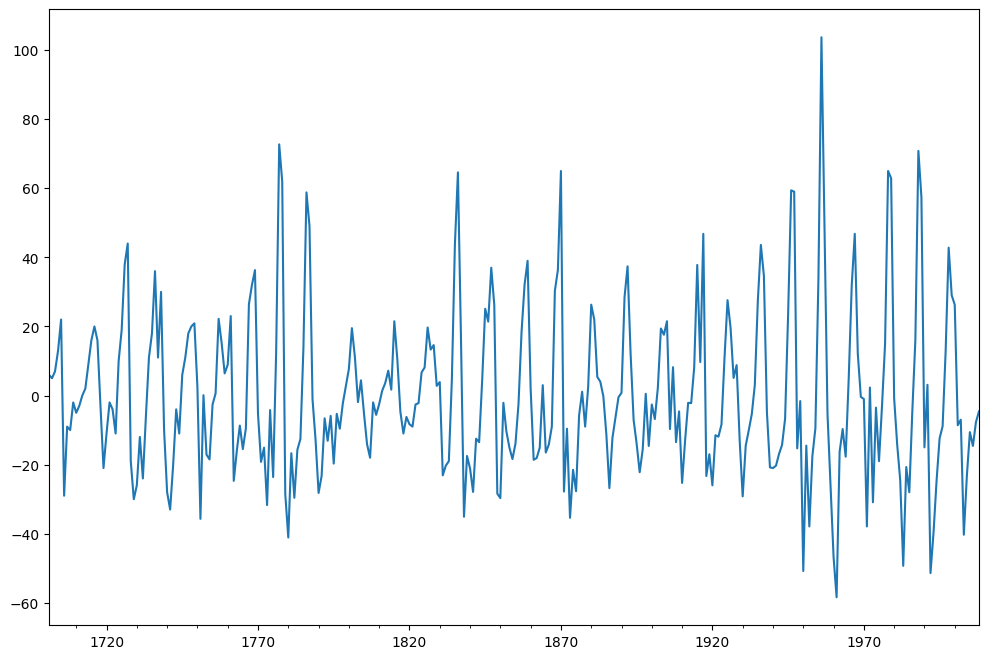
o teste ADF agora é aplicado nesses valores detrended e a estacionariedade é verificada.
:
adf_test(sunspots.dropna())
Results of Dickey-Fuller Test:Test Statistic -1.486166e+01p-value 1.715552e-27#Lags Used 7.000000e+00Number of Observations Used 3.000000e+02Critical Value (1%) -3.452337e+00Critical Value (5%) -2.871223e+00Critical Value (10%) -2.571929e+00dtype: float64
Baseada no p-valor do teste de ADF, há evidências para rejeitar a hipótese nula em favor da alternativa. Portanto, a série é estrita estacionária agora.
o teste KPSS agora é aplicado nesses valores destrendidos e a estacionariedade é verificada.
:
kpss_test(sunspots.dropna())
Results of KPSS Test:Test Statistic 0.021193p-value 0.100000Lags Used 0.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/stattools.py:1911: InterpolationWarning: The test statistic is outside of the range of p-values available in thelook-up table. The actual p-value is greater than the p-value returned. warn_msg.format(direction="greater"), InterpolationWarning
Baseada no p-valor do teste KPSS, a hipótese nula não pode ser rejeitada. Portanto, a série é estacionária.
conclusão¶
são utilizados dois testes para verificar a estacionariedade de uma série temporal, nomeadamente o teste ADF e o teste KPSS. Detrending é realizado usando differencing. A série temporal estacionária da tendência é convertida em séries temporais estacionárias restritas. O modelo de previsão necessário agora pode ser aplicado em dados de séries temporais estacionárias.