O Básico: KNN para classificação e regressão

Ciência de Dados a partir do zero

Dados ou ciência aplicada cursos de estatística, normalmente, começam com modelos lineares, mas em seu caminho, K-vizinhos mais próximos é, provavelmente, o mais simples e amplamente usado modelo conceitual. Os modelos KNN são realmente apenas implementações técnicas de uma intuição comum, que coisas que compartilham características semelhantes tendem a ser, bem, semelhantes. Isso dificilmente é uma visão profunda, mas essas implementações práticas podem ser extremamente poderosas e, crucialmente para alguém que se aproxima de um conjunto de dados Desconhecido, pode lidar com não linearidades sem qualquer Engenharia de dados complicada ou configuração de modelo.

o que

como exemplo ilustrativo, vamos considerar o caso mais simples de usar um modelo KNN como classificador. Digamos que você tenha pontos de dados que se enquadram em uma das três classes. Um exemplo bidimensional pode ser assim:

Você provavelmente pode ver muito claramente que as diferentes classes são agrupadas — o canto superior esquerdo dos gráficos parece pertencer a laranja classe, a mão direita/seção do meio para o azul de classe. Se você recebesse as coordenadas do novo ponto em algum lugar do gráfico e perguntasse a qual classe ele provavelmente pertenceria, na maioria das vezes a resposta seria bem clara. Qualquer ponto no canto superior esquerdo do gráfico provavelmente será laranja, etc.

a tarefa se torna um pouco menos certa entre as classes, no entanto, onde precisamos nos estabelecer em um limite de decisão. Considere o novo ponto adicionado em vermelho abaixo:

este novo ponto deve ser classificado como laranja ou azul? O ponto parece cair entre os dois clusters. Sua primeira intuição pode ser escolher o cluster que está mais próximo do novo ponto. Esta seria a abordagem do “vizinho mais próximo” e, apesar de ser conceitualmente simples, freqüentemente produz previsões bastante sensatas. Qual ponto identificado anteriormente é o novo ponto mais próximo? Pode não ser óbvio só precisa de olhar fixamente para o gráfico, qual é a resposta, mas é mais fácil para o computador para ser executado através de pontos e dar-nos uma resposta:

parece Que o ponto mais próximo está na categoria azul, assim, nosso novo ponto é, provavelmente, demasiado. Esse é o método vizinho mais próximo.

neste ponto, você pode estar se perguntando para que serve o’ k ‘ em K-nearest-neighbors. K é o número de pontos próximos que o modelo examinará ao avaliar um novo ponto. Em nosso exemplo de vizinho mais próximo mais simples, esse valor para k era simplesmente 1-olhamos para o vizinho mais próximo e foi isso. Você poderia, no entanto, ter escolhido olhar para os 2 ou 3 pontos mais próximos. Por que isso é importante e por que alguém definiria k em um número maior? Por um lado, os limites entre as classes podem aumentar um ao lado do outro de maneiras que tornam menos óbvio que o ponto mais próximo nos dará a classificação correta. Considere as regiões azul e verde em nosso exemplo. Na verdade, vamos ampliar-los:

Observe que, enquanto o total regiões parecem suficientemente distintos, seus limites parecem ser um pouco interligados uns com os outros. Esta é uma característica comum de conjuntos de dados com um pouco de ruído. Quando este é o caso, torna-se mais difícil classificar as coisas nas áreas de fronteira. Considere este ponto novo:

por um lado, visualmente ele definitivamente parece mais próximo previamente identificados ponto é azul, que o nosso computador pode facilmente confirmar para nós:

por outro lado, que o mais próximo ponto azul parece um pouco de um outlier em si, longe do centro da região azul e uma espécie de cercado pelo verde pontos. E esse novo ponto está mesmo do lado de fora desse ponto azul! E se olharmos para os três pontos mais próximos do novo ponto vermelho?

Ou até mesmo o mais próximo de cinco pontos para o novo ponto?

Agora parece que o nosso novo ponto é no verde bairro! Aconteceu de ter um ponto azul próximo, mas a preponderância ou pontos próximos são verdes. Nesse caso, talvez faça sentido definir um valor mais alto para k, olhar para um punhado de pontos próximos e fazer com que eles votem de alguma forma na previsão do novo ponto.

o problema que está sendo ilustrado é muito apropriado. Quando K é definido como um, o limite entre quais regiões são identificadas pelo algoritmo como azul e verde é irregular, ele serpenteia de volta com cada ponto individual. O ponto vermelho parece estar na região azul:

Trazendo k até 5, no entanto, suaviza a decisão de fronteira como os diferentes pontos de votação. O ponto vermelho agora parece firmemente no verde bairro:

O trade-off com os valores mais altos de k é a perda de granularidade na decisão de limite. Definir k muito alto tenderá a fornecer limites suaves, mas os limites do mundo real que você está tentando modelar podem não ser perfeitamente suaves.

praticamente falando, podemos usar o mesmo tipo de abordagem de vizinhos mais próximos para regressões, onde queremos um valor individual em vez de uma classificação. Considere a seguinte regressão abaixo:

Os dados foram gerados aleatoriamente, mas foi gerado para ser linear, para um modelo de regressão linear seria, naturalmente, ajuste este dado bem. Quero salientar, no entanto, que você pode aproximar os resultados do método linear de uma maneira conceitualmente mais simples com uma abordagem K-nearest neighbors. Nossa ‘regressão’ neste caso não será uma única fórmula como um modelo OLS nos daria, mas sim um valor de saída melhor previsto para qualquer entrada. Considere o valor de -.75 sobre o eixo x, que eu marquei com uma linha vertical:

Sem resolver qualquer equações podemos chegar a uma aproximação razoável do que a saída deve ser apenas considerando os pontos próximos:

faz sentido que o valor previsto deve ser perto desses pontos, não muito inferior ou superior. Talvez uma boa previsão seja a média desses pontos:

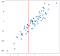
Você pode imaginar fazendo isso para todos os possíveis valores de entrada e chegando com previsões em qualquer lugar:

Conectando todas essas previsões com uma linha nos dá o nosso regressão:

neste caso, os resultados não são uma linha limpa, mas eles não rastrear a inclinação ascendente dos dados razoavelmente bem. Isso pode não parecer terrivelmente impressionante, mas um benefício da simplicidade dessa implementação é que ela lida bem com a não linearidade. Considere esta nova coleção de pontos:

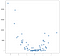
Estes pontos foram gerados por simplesmente elevar os valores do exemplo anterior, mas suponha que você veio através de um conjunto de dados como este em estado selvagem. Obviamente, não é de natureza linear e, embora um modelo de estilo OLS possa lidar facilmente com esse tipo de dados, ele requer o uso de termos não lineares ou de interação, o que significa que o cientista de dados deve tomar algumas decisões sobre que tipo de engenharia de dados executar. A abordagem KNN não requer mais decisões-o mesmo código que usei no exemplo linear pode ser reutilizado inteiramente nos novos dados para produzir um conjunto viável de previsões:

tal como acontece com os exemplos do Classificador, definir um valor mais alto K nos ajuda a evitar o overfit, embora você possa começar a perder o poder preditivo na margem, particularmente nas bordas do seu conjunto de dados. Considere o primeiro conjunto de dados de exemplo com previsões feitas com K definido como um, que é uma abordagem vizinha mais próxima:

Nossas previsões do salto de forma irregular em torno de como o modelo de saltos a partir de um ponto no conjunto de dados para o próximo. Por outro lado, a definição de k em dez, de modo que dez o total de pontos são calculados em média para a previsão de rendimento de uma forma muito mais suave passeio:

Geralmente o que fica melhor, mas você pode ver algo de um problema nas bordas dos dados. Como nosso modelo está levando em consideração tantos pontos para qualquer previsão, quando nos aproximamos de uma das bordas de nossa amostra, nossas previsões começam a piorar. Podemos resolver esse problema um pouco ponderando nossas previsões para os pontos mais próximos, embora isso venha com suas próprias compensações.

como

ao configurar um modelo KNN, há apenas um punhado de parâmetros que precisam ser escolhidos/podem ser ajustados para melhorar o desempenho.

K: o número de vizinhos: Conforme discutido, o aumento de K tenderá a suavizar os limites de decisão, evitando o overfit ao custo de alguma resolução. Não existe um valor único de k que funcione para cada conjunto de dados. Para modelos de classificação, especialmente se existem apenas duas classes, um número ímpar é geralmente escolhido para k. Este é, portanto, o algoritmo nunca é executado em um “empate”: por exemplo, ele olha para o mais próximo de quatro pontos e descobre que dois deles estão na categoria azul e dois estão no vermelho categoria.

distância métrica: Existem, ao que parece, maneiras diferentes de medir o quão “próximos” dois pontos são um do outro, e as diferenças entre esses métodos podem se tornar significativas em dimensões mais altas. Mais comumente usado é distância Euclidiana, o tipo padrão que você pode ter aprendido no ensino médio usando o teorema de Pitágoras. Outra métrica é a chamada “distância de Manhattan”, que mede a distância percorrida em cada direção cardinal, em vez de ao longo da diagonal (como se você estivesse caminhando de um cruzamento de rua em Manhattan para outro e tivesse que seguir a grade de rua em vez de ser capaz de tomar a rota mais curta “enquanto o corvo voa”). De forma mais geral, essas são, na verdade, as duas formas do que é chamado de ‘distância de Minkowski’, cuja fórmula é:

Quando p é definido como 1, esta fórmula é a mesma distância de Manhattan, e quando definido para dois, distância Euclidiana.

Pesos: uma maneira de resolver a questão de um possível ‘empate’ quando o algoritmo vota em uma classe e o problema em que nossas previsões de regressão pioraram para as bordas do conjunto de dados é introduzindo ponderação. Com pesos, os pontos próximos contarão mais do que os pontos mais distantes. O algoritmo ainda vai olhar para todos os K vizinhos mais próximos, mas os vizinhos mais próximos terão mais de um voto do que aqueles mais longe. Esta não é uma solução perfeita e traz à tona a possibilidade de adaptação excessiva novamente. Considere a possibilidade de regressão exemplo, desta vez com pesos:

as Nossas previsões vá para a direita para a borda do conjunto de dados agora, mas você pode ver que as nossas previsões agora swing muito mais perto de pontos individuais. O método ponderado funciona razoavelmente bem quando você está entre os pontos, mas à medida que você se aproxima cada vez mais de qualquer ponto específico, o valor desse ponto tem cada vez mais influência na previsão do algoritmo. Se você chegar perto o suficiente de um ponto, é quase como definir k para um, já que esse ponto tem tanta influência.

dimensionamento / normalização: um último ponto, mas crucialmente importante, é que os modelos KNN podem ser descartados se diferentes variáveis de recurso tiverem escalas muito diferentes. Considere um modelo que tenta prever, digamos, o preço de venda de uma casa no mercado com base em características como o número de quartos e a metragem quadrada total da casa, etc. Há mais variação no número de pés quadrados em uma casa do que no número de quartos. Normalmente, as casas têm apenas um pequeno punhado de quartos, e nem mesmo a maior mansão terá dezenas ou centenas de quartos. Os pés quadrados, por outro lado, são relativamente pequenos, então as casas podem variar de perto, digamos, 1.000 sq feat no lado pequeno a dezenas de milhares de pés quadrados no lado grande.

considere a comparação entre uma casa de 2.000 pés quadrados com 2 quartos e uma casa de 2.010 pés quadrados com dois quartos — 10 metros quadrados. pés dificilmente faz a diferença. Por outro lado, uma casa de 2.000 pés quadrados com três quartos é muito diferente e representa um layout muito diferente e possivelmente mais apertado. Um computador ingênuo não teria o contexto para entender isso, no entanto. Diria que o quarto 3 é apenas ‘ uma ‘unidade de distância do Quarto 2, enquanto o rodapé 2,010 sq é’ Dez ‘ de distância do rodapé 2,000 sq. Para evitar isso, os dados dos recursos devem ser dimensionados antes de implementar um modelo KNN.

pontos fortes e fracos

os modelos KNN são fáceis de implementar e lidar bem com não linearidades. Ajustar o modelo também tende a ser rápido: o computador não precisa calcular nenhum parâmetro ou valor específico, afinal. A troca aqui é que, embora o modelo seja rápido de configurar, é mais lento prever, pois, para prever um resultado para um novo valor, ele precisará pesquisar todos os pontos em seu conjunto de treinamento para encontrar os mais próximos. Para grandes conjuntos de dados, o KNN pode, portanto, ser um método relativamente lento em comparação com outras regressões que podem levar mais tempo para caber, mas depois fazer suas previsões com cálculos relativamente diretos.

um outro problema com um modelo KNN é que ele não tem interpretabilidade. Uma regressão linear OLS terá coeficientes claramente interpretáveis que podem dar alguma indicação do ‘tamanho do efeito’ de um determinado recurso (embora, algum cuidado deva ser tomado ao atribuir causalidade). Perguntar quais recursos têm o maior efeito realmente não faz sentido para um modelo KNN, no entanto. Em parte por causa disso, os modelos KNN também não podem realmente ser usados para seleção de recursos, da maneira que uma regressão linear com um termo de função de custo adicional, como ridge ou lasso, pode ser, ou a maneira como uma árvore de decisão escolhe implicitamente quais recursos parecem mais valiosos.