elementele de bază: KNN pentru clasificare și regresie

știința datelor de la zero

știința datelor sau cursurile de Statistică Aplicată încep de obicei cu modele liniare, dar în felul său, k-neighbors neighbors este probabil cel mai simplu model utilizat pe scară largă conceptual. Modelele KNN sunt într-adevăr doar implementări tehnice ale unei intuiții comune, că lucrurile care împărtășesc caracteristici similare tind să fie, bine, similare. Aceasta nu este o perspectivă profundă, totuși aceste implementări practice pot fi extrem de puternice și, în mod crucial pentru cineva care se apropie de un set de date necunoscut, poate gestiona neliniaritățile fără o inginerie complicată a datelor sau un model configurat.

ce

ca exemplu ilustrativ, să luăm în considerare cel mai simplu caz de utilizare a unui model KNN ca clasificator. Să presupunem că aveți puncte de date care se încadrează într-una din cele trei clase. Un exemplu bidimensional poate arăta astfel:

probabil puteți vedea destul de clar că diferitele clase sunt grupate împreună — colțul din stânga sus al graficelor pare să aparțină clasei portocalii, secțiunea dreaptă/mijlocie clasei albastre. Dacă vi s-ar da coordonatele punctului nou undeva pe grafic și ați întreba din ce clasă este probabil să aparțină, de cele mai multe ori răspunsul ar fi destul de clar. Orice punct din colțul din stânga sus al graficului este probabil să fie portocaliu etc.

sarcina devine un pic mai puțin sigur între clase, cu toate acestea, în cazul în care avem nevoie să se stabilească pe o limită de decizie. Luați în considerare noul punct adăugat în roșu de mai jos:

acest nou punct ar trebui clasificat ca portocaliu sau albastru? Punctul pare să se încadreze între cele două clustere. Prima ta intuiție ar putea fi să alegi clusterul care este mai aproape de noul punct. Aceasta ar fi abordarea celui mai apropiat vecin și, în ciuda faptului că este simplu din punct de vedere conceptual, produce adesea predicții destul de sensibile. Care punct identificat anterior este cel mai apropiat punct nou? S-ar putea să nu fie evident doar să privim graficul care este răspunsul, dar este ușor pentru computer să ruleze prin puncte și să ne dea un răspuns:

se pare că cel mai apropiat punct este în categoria albastră, deci noul nostru punct este probabil și el. Aceasta este metoda vecinului cel mai apropiat.

în acest moment s-ar putea să vă întrebați pentru ce este ‘k’ în K-neighbors-neighbors. K este numărul de puncte din apropiere pe care modelul le va analiza atunci când evaluează un punct nou. În cel mai simplu exemplu de vecin apropiat, această valoare pentru k a fost pur și simplu 1 — ne-am uitat la cel mai apropiat vecin și asta a fost. Ai putea, cu toate acestea, au ales să se uite la cel mai apropiat 2 sau 3 puncte. De ce este important acest lucru și de ce ar stabili cineva k la un număr mai mare? În primul rând, granițele dintre clase s-ar putea ciocni una lângă alta în moduri care fac mai puțin evident că cel mai apropiat punct ne va oferi clasificarea corectă. Luați în considerare regiunile albastre și verzi din exemplul nostru. De fapt, să mărim pe ele:

observați că, deși regiunile generale par suficient de distincte, limitele lor par a fi puțin împletite între ele. Aceasta este o caracteristică comună a seturilor de date cu un pic de zgomot. Când acesta este cazul, devine mai greu să clasificăm lucrurile în zonele de graniță. Luați în considerare acest nou punct:

pe de o parte, vizual se pare că cel mai apropiat punct identificat anterior este albastru, pe care computerul nostru îl poate confirma cu ușurință pentru noi:

pe de altă parte, cel mai apropiat punct albastru pare a fi un pic de outlier în sine, departe de centrul regiunii albastre și un fel de înconjurat de puncte verzi. Și acest nou punct este chiar în exteriorul acelui punct albastru! Ce se întâmplă dacă ne-am uita la cele trei puncte Cele mai apropiate de noul punct roșu?

sau chiar cele mai apropiate cinci puncte de noul punct?

acum se pare că noul nostru punct este într-un cartier verde! S-a întâmplat să aibă un punct albastru din apropiere, dar preponderența sau punctele din apropiere sunt verzi. În acest caz, poate că ar avea sens să setați o valoare mai mare pentru k, să vă uitați la o mână de puncte din apropiere și să le cereți să voteze cumva Predicția pentru noul punct.

problema ilustrată este prea potrivită. Când k este setat la unul, granița dintre regiunile identificate de algoritm ca albastru și verde este denivelată, se șerpuiește înapoi cu fiecare punct individual. Punctul roșu arată ca și cum ar putea fi în regiunea albastră:

aducând k până la 5, cu toate acestea, netezește limita deciziei pe măsură ce votează diferitele puncte din apropiere. Punctul roșu pare acum ferm în Cartierul Verde:

compromisul cu valori mai mari ale k este pierderea granularității în limita deciziei. Setarea k foarte mare va tinde să vă ofere limite netede, dar limitele lumii reale pe care încercați să le modelați s-ar putea să nu fie perfect netede.

practic, putem folosi același tip de abordare a vecinilor apropiați pentru regresii, unde dorim mai degrabă o valoare individuală decât o clasificare. Luați în considerare următoarea regresie de mai jos:

datele au fost generate aleatoriu, dar au fost generate pentru a fi liniare, astfel încât un model de regresie liniară s-ar potrivi în mod natural acestor date. Vreau să subliniez, totuși, că puteți aproxima rezultatele metodei liniare într-un mod conceptual mai simplu, cu o abordare k-cea mai apropiată vecini. Regresia noastră în acest caz nu va fi o singură formulă, așa cum ne-ar oferi un model OLS, ci mai degrabă o valoare de ieșire cea mai bună prezisă pentru orice intrare dată. Luați în considerare valoarea -.75 pe axa x, pe care am marcat-o cu o linie verticală:

fără a rezolva orice ecuații putem ajunge la o aproximare rezonabilă a ceea ce ar trebui să fie de ieșire doar luând în considerare punctele din apropiere:

este logic ca valoarea prezisă să fie aproape de aceste puncte, nu mult mai mică sau mai mare. Poate că o predicție bună ar fi media acestor puncte:

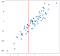
vă puteți imagina făcând acest lucru pentru toate valorile posibile de intrare și venind cu predicții peste tot:

conectarea tuturor acestor predicții cu o linie ne dă regresia noastră:

în acest caz, rezultatele nu sunt o linie curată, dar urmăresc în mod rezonabil panta ascendentă a datelor. Acest lucru poate să nu pară teribil de impresionant, dar un beneficiu al simplității acestei implementări este că gestionează bine neliniaritatea. Luați în considerare această nouă colecție de puncte:

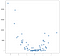
aceste puncte au fost generate prin simpla pătrare a valorilor din exemplul anterior, dar să presupunem că ați dat peste un set de date ca acesta în sălbăticie. Evident, nu are o natură liniară și, deși un model de stil OLS poate gestiona cu ușurință acest tip de date, necesită utilizarea unor termeni neliniari sau de interacțiune, ceea ce înseamnă că omul de știință de date trebuie să ia unele decizii cu privire la ce fel de Inginerie a datelor să efectueze. Abordarea KNN nu necesită alte decizii — același cod pe care l-am folosit pe exemplul liniar poate fi reutilizat în întregime pe noile date pentru a obține un set funcțional de predicții:

ca și în cazul exemplelor de clasificator, setarea unei valori mai mari k ne ajută să evităm suprasolicitarea, deși este posibil să începeți să pierdeți puterea predictivă pe margine, în special în jurul marginilor setului dvs. de date. Luați în considerare primul exemplu de set de date cu predicții făcute cu K setat la unul, adică o abordare a celui mai apropiat vecin:

previziunile noastre sari haotic în jurul ca modelul sare de la un punct în setul de date la altul. În schimb, setarea k la zece, astfel încât zece puncte totale să fie mediate împreună pentru predicție produce o călătorie mult mai lină:

în general, arată mai bine, dar puteți vedea o problemă la marginile datelor. Deoarece modelul nostru ia în considerare atât de multe puncte pentru orice predicție dată, când ne apropiem de unul dintre marginile eșantionului nostru, predicțiile noastre încep să se înrăutățească. Putem aborda această problemă oarecum prin ponderarea predicțiilor noastre la punctele mai apropiate, deși acest lucru vine cu propriile compromisuri.

cum

la configurarea unui model KNN există doar o mână de parametri care trebuie aleși/pot fi optimizați pentru a îmbunătăți performanța.

K: numărul de vecini: După cum sa discutat, creșterea K va tinde să netezească limitele deciziei, evitând suprasolicitarea cu prețul unei rezoluții. Nu există o singură valoare a lui k care să funcționeze pentru fiecare set de date. Pentru modelele de clasificare, mai ales dacă există doar două clase, un număr impar este de obicei ales pentru k. astfel, algoritmul nu intră niciodată într-o egalitate: de exemplu, se uită la cele mai apropiate patru puncte și constată că două dintre ele sunt în categoria albastră și două sunt în categoria roșie.

distanța metrică: Există, după cum se dovedește, moduri diferite de a măsura cât de apropiate sunt două puncte una de cealaltă, iar diferențele dintre aceste metode pot deveni semnificative în dimensiuni superioare. Cel mai frecvent utilizat este distanța euclidiană, genul standard pe care l-ați învățat în școala medie folosind teorema lui Pitagora. O altă metrică este așa-numita ‘distanța Manhattan’, care măsoară distanța luată în fiecare direcție cardinală, mai degrabă decât de-a lungul diagonalei (ca și cum ați merge de la o intersecție de stradă din Manhattan la alta și a trebuit să urmați grila stradală, mai degrabă decât să puteți lua cea mai scurtă’ pe măsură ce cioara zboară ‘ traseu). Mai general, acestea sunt de fapt ambele forme ale ceea ce se numește ‘distanța Minkowski’, a cărui formulă este:

când p este setat la 1, Această formulă este aceeași cu distanța Manhattan, iar când este setată la două, distanța euclidiană.

ponderi: o modalitate de a rezolva atât problema unei posibile ‘legături’ atunci când algoritmul votează o clasă, cât și problema în care predicțiile noastre de regresie s-au înrăutățit spre marginile setului de date este prin introducerea ponderării. Cu greutăți, punctele apropiate vor conta mai mult decât punctele mai îndepărtate. Algoritmul se va uita în continuare la toți cei mai apropiați vecini k, dar vecinii mai apropiați vor avea mai mult de un vot decât cei mai departe. Aceasta nu este o soluție perfectă și aduce posibilitatea de a suprasolicita din nou. Luați în considerare exemplul nostru de regresie, de data aceasta cu greutăți:

predicțiile noastre merg chiar la marginea setului de date acum, dar puteți vedea că predicțiile noastre se apropie acum mult mai mult de punctele individuale. Metoda ponderată funcționează destul de bine atunci când vă aflați între puncte, dar pe măsură ce vă apropiați din ce în ce mai mult de un anumit punct, valoarea acelui punct are din ce în ce mai multă influență asupra predicției algoritmului. Dacă vă apropiați suficient de mult de un punct, este aproape ca și cum ați seta k la unul, deoarece acel punct are atât de multă influență.

scalare/normalizare: un ultim punct, dar extrem de important, este că modelele KNN pot fi aruncate dacă diferite variabile de caracteristici au scale foarte diferite. Luați în considerare un model care încearcă să prezică, să zicem, prețul de vânzare al unei case pe piață pe baza unor caracteristici precum numărul de dormitoare și suprafața totală a casei etc. Există mai multe variații în numărul de metri pătrați într-o casă decât există în numărul de dormitoare. De obicei, casele au doar o mână mică de dormitoare și nici măcar cel mai mare conac nu va avea zeci sau sute de dormitoare. Picioarele pătrate, pe de altă parte, sunt relativ mici, astfel încât casele pot varia de la aproape, să zicem, 1.000 de metri pătrați pe partea mică până la zeci de mii de metri pătrați pe partea mare.

luați în considerare comparația dintre o casă de 2.000 mp cu 2 dormitoare și o casă de 2.010 mp cu două dormitoare — 10 mp. picioarele abia fac diferența. În schimb, o casă de 2.000 de metri pătrați cu trei dormitoare este foarte diferită și reprezintă un aspect foarte diferit și, eventual, mai înghesuit. Un computer naiv nu ar avea contextul să înțeleagă asta. S-ar spune că 3 dormitor este doar ‘o’ unitate departe de 2 dormitor, în timp ce 2,010 sq subsol este ‘zece’ departe de 2,000 sq subsol. Pentru a evita acest lucru, datele despre caracteristici ar trebui scalate înainte de a implementa un model KNN.

puncte forte și puncte slabe

modelele KNN sunt ușor de implementat și manipulate bine neliniaritățile. Montarea modelului tinde, de asemenea, să fie rapidă: computerul nu trebuie să calculeze parametri sau valori particulare, la urma urmei. Compromisul aici este că, în timp ce modelul este rapid de configurat, este mai lent de prezis, deoarece pentru a prezice un rezultat pentru o nouă valoare, va trebui să caute prin toate punctele din setul său de antrenament pentru a găsi cele mai apropiate. Pentru seturi de date mari, KNN poate fi, prin urmare, o metodă relativ lentă în comparație cu alte regresii care pot dura mai mult timp pentru a se potrivi, dar apoi își fac predicțiile cu calcule relativ simple.

o altă problemă cu un model KNN este că îi lipsește interpretabilitatea. O regresie liniară OLS va avea coeficienți clar interpretabili care pot da ei înșiși o indicație a dimensiunii efectului unei caracteristici date (deși, trebuie luată o anumită precauție atunci când se atribuie cauzalitatea). Cu toate acestea, întrebarea care caracteristici au cel mai mare efect nu are sens pentru un model KNN. Parțial din această cauză, modelele KNN nu pot fi utilizate cu adevărat pentru selectarea caracteristicilor, în modul în care poate fi o regresie liniară cu un termen de funcție de cost adăugat, cum ar fi ridge sau lasso, sau modul în care un arbore de decizie alege implicit caracteristicile care par cele mai valoroase.