energia kinetyczna jest energią ruchu. Wyrażenie dla energii kinetycznej otrzymuje się, patrząc na przypadek obiektu, który jest uniesiony na pewną względną wysokość (w ten sposób praca jest wykonywana na tym obiekcie), a następnie pozostawiony do upadku.
kluczowe terminy
o energia kinetyczna
cele
o uzyskaj wyrażenie dla energii kinetycznej z fizyki koncepcji pracy
o zrozum związek pracy z energią kinetyczną
o Oblicz energię kinetyczną różnych obiektów
zaczynajmy!
odnosząca się do pracy i energii kinetycznej
w pewnym sensie praca jest ilością energii włożoną w zadanie (lub, być może, „włożoną w obiekt”). Wyobraźmy sobie na przykład, że podnosimy jakiś przedmiot z podłogi i podnosimy go na określoną wysokość; wykonaliśmy pewną pracę nad tym obiektem. Jeśli jednak odpuścimy, przyspiesza, tak jakby praca, którą wykonaliśmy przy podnoszeniu obiektu, zamieniała się w ruch. Za pomocą tego przykładu możemy uzyskać definicję energii kinetycznej, która jest energią ruchu. Definicja ta, jak zobaczymy, jest ściśle związana z tym, jak zdefiniowaliśmy pracę.
najpierw rozważmy obiekt: kulę o masie m. wybierzemy piłkę ze stołu i podniesiemy ją o odległość H powyżej tego stołu, jak pokazano poniżej. W związku z tym wykonaliśmy wiele prac W = mgh (wynik ten jest iloczynem wielkości wektora przemieszczenia (h) i przyłożonej siły (mg) – odpowiednie wektory są równoległe).
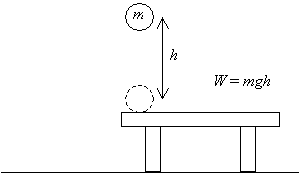
teraz, jeśli zwolnimy tę piłkę i pozwolimy jej spaść z wysokości h nad stołem, po powrocie do pierwotnej wysokości (poziomu stołu), będzie miała pewną prędkość v wynikającą z przyspieszenia spowodowanego grawitacją.
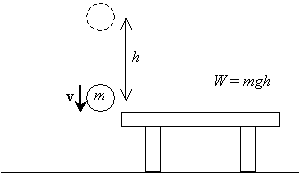
chcemy obliczyć tę prędkość (lub prędkość, technicznie — czasami możemy zastąpić termin prędkość dla prędkości, ale zawsze należy pamiętać, że prędkość jest w rzeczywistości wektorem, a prędkość jest wielkością prędkości). Wiemy, że przyspieszenie spowodowane grawitacją jest stałe, a prędkość początkowa kuli jest zerowa (jest nieruchoma, zanim zostanie uwolniona). Zakładamy, że początkowa wysokość piłki wynosi h, a jej końcowa wysokość wynosi zero (poziom stołu). Aby obliczyć prędkość poprzez wyprowadzenie odpowiednich wzorów, wymagamy użycia podstawowego rachunku całkowego. (Jeśli jesteś zaawansowanym studentem lub szukasz dodatkowego wyzwania, możesz spróbować samodzielnie opracować te formuły w powyższych warunkach. Po prostu zauważ, że prędkość v Kuli jest szybkością zmiany jej położenia x w funkcji czasu t, ![]() , a przyspieszenie a jest szybkością zmiany prędkości,
, a przyspieszenie a jest szybkością zmiany prędkości, ![]() .)
.)
![]()
![]()
te wzory wyrażają prędkość jako funkcję czasu, v(t), A pozycję (wysokość) jako funkcję czasu, x(t), pod względem przyspieszenia A, wysokości h i czasu t. wiemy, że A = –g, ponieważ piłka jest przyspieszana tylko przez grawitację, a to przyspieszenie jest w dół (stąd znak ujemny). Ostateczna pozycja piłki wynosi zero metrów, lub x (t) = 0. Obliczmy t, ilość czasu między uwolnieniem piłki a jej przybyciem na poziom stołu.
![]()
![]()
![]()
teraz obliczmy prędkość piłki w tym momencie.
![]()
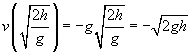
porównajmy teraz ten wynik z oryginalnie wykonaną pracą nad obiektem: w = mgh. Zauważ, jak bliskie są te dwa wyrażenia; w rzeczywistości jedynym czynnikiem, którego brakuje w prędkości, jest masa kuli, m. gdybyśmy do kwadratu prędkość pomnożyli przez m, a następnie podzielili przez 2, w rzeczywistości mielibyśmy to samo wyrażenie co praca!
![]()
w ten sposób możemy zobaczyć w pewnym sensie, jak można wyprowadzić definicję energii kinetycznej. Energia kinetyczna K obiektu jest skalarem zdefiniowanym w następujący sposób, gdzie m jest masą obiektu, a v jest jego prędkością:
![]()
jak się okazuje, energia kinetyczna jest pracą wykonywaną na obiekcie przez siłę netto na ten obiekt. Tak więc, chociaż kobieta może wykonać pewną pracę na obiekcie, podnosząc go z jednej wysokości na drugą, Siła netto na ten obiekt jest zerowa (kobieta stosuje siłę równą, ale przeciwną w kierunku grawitacji). Tak więc nie ma zmian w energii kinetycznej. Jeśli jednak obiekt zostanie uwolniony i opadnie, zyskuje energię kinetyczną, ponieważ siła netto na niego jest po prostu siłą grawitacji (pojedyncza Siła). Tak więc, aby zrozumieć związek energii kinetycznej z pracą, musimy nieco udoskonalić naszą koncepcję pracy. Jeśli zdefiniujemy pracę W jako całkowitą pracę wykonaną na obiekcie przez wszystkie siły (innymi słowy, pracę wykonaną na obiekcie przez siłę netto), to następujący związek między pracą W a początkowymi i końcowymi energiami kinetycznymi (Ki i Kf) utrzymuje się.
![]() gdzie
gdzie ![]()
tak więc praca netto wykonana na obiekcie jest równa zmianie energii kinetycznej tego obiektu (ΔK). Poniższe problemy praktyczne dają możliwość przetestowania i zastosowania twojego rozumienia pojęć pracy i energii kinetycznej.
Problem Z Praktyką: Pocisk o masie 1 kilograma porusza się z prędkością 5 metrów na sekundę. Jaką prędkość musi przemieścić pocisk o masie 0,1 kilograma, aby osiągnąć taką samą energię kinetyczną?
rozwiązanie :najpierw obliczmy energię kinetyczną bardziej masywnego (1 kg) pocisku.
![]()
możemy teraz obliczyć prędkość mniej masywnego obiektu tak, że ma on taką samą energię kinetyczną, K.
![]()
![]()
![]()
Problem z praktyką: mężczyzna podnosi 15-kilogramową wagę na wysokość dwóch metrów nad ziemią, zanim ją zrzuci. Jaka jest prędkość, zanim ciężar zetknie się z podłożem?
rozwiązanie: narysujmy diagram ilustrujący siły działające na Obiekt, gdy jest on podnoszony i upada; siły te obejmują grawitację (Fg) i siłę w górę, którą człowiek stosuje (Fu).
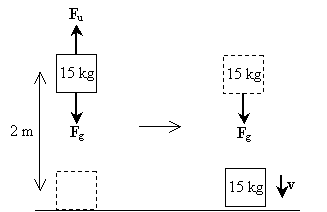
zauważ, że pierwszy etap procesu (podnoszenie ciężaru) nie wymaga siły netto działającej na przedmiot-siła spowodowana grawitacją jest równoważona przez siłę, którą człowiek stosuje w podnoszeniu ciężaru. W drugim kroku jednak ciężar doświadcza jedynie siły grawitacji. Siła netto, w tym przypadku, jest zatem mg w kierunku w dół. Jako takie, prędkość obiektu jest również w kierunku w dół. Praca wykonana na wadze w wyniku grawitacji jest po prostu mgh; jest to również całkowita praca wykonana na wadze w całym procesie. Zauważ, że początkowa energia kinetyczna masy wynosi zero, ponieważ ma zerową prędkość. Obliczmy prędkość stosując zależność między pracą netto a zmianą energii kinetycznej.