podstawy: KNN do klasyfikacji i regresji

Data Science od podstaw

kursy Data science lub statystyki stosowanej zazwyczaj zaczynają się od modeli liniowych, ale na swój sposób K-nearest neighbours jest prawdopodobnie najprostszym powszechnie stosowanym modelem koncepcyjnie. Modele KNN są tak naprawdę tylko techniczną implementacją wspólnej intuicji, że rzeczy, które mają podobne cechy, są zwykle, cóż, podobne. Nie jest to głęboki wgląd, ale te praktyczne wdrożenia mogą być niezwykle potężne, a co najważniejsze dla kogoś, kto zbliża się do nieznanego zbioru danych, może obsługiwać Nieliniowość bez skomplikowanej inżynierii danych lub konfiguracji modelu.

co

jako przykład ilustracyjny rozważmy najprostszy przypadek użycia modelu KNN jako klasyfikatora. Załóżmy, że masz punkty danych, które należą do jednej z trzech klas. Dwuwymiarowy przykład może wyglądać następująco:

prawdopodobnie widać całkiem wyraźnie, że różne klasy są zgrupowane razem — lewy górny róg Wykresów wydaje się należeć do klasy pomarańczowej, prawy/środkowy do klasy niebieskiej. Gdybyś otrzymał współrzędne nowego punktu gdzieś na wykresie i zapytał, do której klasy prawdopodobnie należy, przez większość czasu odpowiedź byłaby dość jasna. Każdy punkt w lewym górnym rogu wykresu może być pomarańczowy, itd.

zadanie staje się jednak nieco mniej pewne między klasami, gdzie musimy rozstrzygnąć granicę decyzji. Rozważ nowy punkt dodany na Czerwono poniżej:

czy ten nowy punkt powinien być klasyfikowany jako pomarańczowy czy Niebieski? Wydaje się, że punkt znajduje się pomiędzy tymi dwoma skupiskami. Pierwszą intuicją może być wybór klastra, który jest bliżej nowego punktu. Byłoby to podejście „najbliższego sąsiada” i pomimo tego, że jest koncepcyjnie proste, często daje całkiem sensowne prognozy. Który wcześniej zidentyfikowany punkt jest najbliższy nowemu punktowi? Może nie jest oczywiste, że wystarczy spojrzeć na wykres, jaka jest odpowiedź, ale łatwo jest komputerowi przejrzeć punkty i dać nam odpowiedź:

wygląda na to, że najbliższy punkt znajduje się w kategorii niebieskiej, więc nasz nowy punkt prawdopodobnie również. To jest metoda najbliższego sąsiada.

w tym momencie możesz się zastanawiać, do czego służy ” k ” W K-nearest-neighbours. K to liczba pobliskich punktów, na które model będzie patrzył podczas oceny nowego punktu. W naszym najprostszym przykładzie najbliższego sąsiada, ta wartość dla k wynosiła po prostu 1-spojrzeliśmy na najbliższego sąsiada i to wszystko. Możesz jednak wybrać, aby spojrzeć na najbliższe 2 lub 3 punkty. Dlaczego jest to ważne i dlaczego ktoś miałby ustawić K na wyższą liczbę? Po pierwsze, granice między klasami mogą podskoczyć obok siebie w taki sposób, że mniej oczywiste jest, że najbliższy punkt da nam właściwą klasyfikację. Weźmy pod uwagę niebieskie i zielone regiony w naszym przykładzie. W rzeczywistości, przybliżymy je:

zauważ, że chociaż ogólne regiony wydają się wystarczająco wyraźne, ich granice wydają się być trochę ze sobą powiązane. Jest to powszechna cecha zestawów danych z odrobiną szumu. Kiedy tak się dzieje, trudniej jest klasyfikować rzeczy w obszarach granicznych. Rozważ ten nowy punkt:

z jednej strony wizualnie zdecydowanie wygląda tak, jakby najbliżej zidentyfikowanym wcześniej punktem był niebieski, co nasz komputer może nam łatwo potwierdzić:

z drugiej strony, ten najbliższy punkt niebieski wydaje się trochę bardziej odległy, daleko od centrum regionu niebieskiego i jakby otoczony zielonymi punktami. A ten nowy punkt jest nawet na zewnątrz tego niebieskiego punktu! Co jeśli spojrzymy na trzy najbliższe punkty do nowego czerwonego punktu?

lub nawet najbliższe pięć punktów do nowego punktu?

teraz wydaje się, że nasz nowy punkt jest w zielonej okolicy! Zdarzało się, że miał w pobliżu niebieski punkt, ale przewaga lub pobliskie punkty są zielone. W tym przypadku, może sensowne byłoby ustawienie wyższej wartości dla k, przyjrzenie się kilku pobliskim punktom i poproszenie ich o głosowanie nad przewidywaniem nowego punktu.

ilustrowana sprawa jest przesadzona. Gdy k jest ustawione na 1, granica między którymi regiony są identyfikowane przez algorytm jako niebieskie i zielone jest wyboista, przesuwa się do przodu z każdym pojedynczym punktem. Czerwony punkt wygląda tak, jakby znajdował się w obszarze niebieskim:

podnosząc k do 5, jednak wygładza granicę decyzji, gdy głosują różne pobliskie punkty. Czerwony punkt wydaje się teraz mocno w zielonej okolicy:

kompromis z wyższymi wartościami k to utrata ziarnistości w granicy decyzji. Ustawienie k bardzo wysoko daje gładkie granice, ale granice świata rzeczywistego, które próbujesz modelować, mogą nie być idealnie gładkie.

praktycznie rzecz biorąc, możemy użyć tego samego rodzaju podejścia najbliższych sąsiadów do regresji, gdzie chcemy indywidualnej wartości, a nie klasyfikacji. Rozważ następującą regresję poniżej:

dane zostały wygenerowane losowo, ale zostały wygenerowane jako liniowe, więc model regresji liniowej naturalnie pasowałby do tych danych dobrze. Chcę jednak podkreślić, że można przybliżać wyniki metody liniowej w koncepcyjnie prostszy sposób przy pomocy podejścia K-najbliżsi sąsiedzi. Nasza „regresja” w tym przypadku nie będzie pojedynczą formułą, jaką dałby nam model OLS, ale raczej najlepszą przewidywaną wartością wyjściową dla danego wejścia. Rozważ wartość -.75 na osi x, którą zaznaczyłem pionową linią:

bez rozwiązywania równań możemy dojść do rozsądnego przybliżenia tego, co powinno być wynikiem, po prostu biorąc pod uwagę pobliskie punkty:

sensowne jest, że przewidywana wartość powinna znajdować się w pobliżu tych punktów, nie dużo niższa lub wyższa. Być może dobrą prognozą będzie średnia tych punktów:

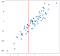
możesz sobie wyobrazić robienie tego dla wszystkich możliwych wartości wejściowych i wymyślanie prognoz wszędzie:

połączenie tych wszystkich prognoz z linią daje nam regresję:

w tym przypadku wyniki nie są czystą linią, ale dość dobrze śledzą nachylenie danych w górę. Może nie wydaje się to imponujące, ale jedną z zalet prostoty tej implementacji jest to, że dobrze radzi sobie z nieliniowością. Rozważ ten nowy zbiór punktów:

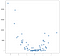
punkty te zostały wygenerowane przez po prostu wyrównanie do kwadratu wartości z poprzedniego przykładu, ale załóżmy, że natknąłeś się na taki zestaw danych w wild. Oczywiście nie ma on charakteru liniowego i chociaż model w stylu OLS może z łatwością obsługiwać tego rodzaju dane, wymaga użycia terminów nieliniowych lub interakcji, co oznacza, że analityk danych musi podjąć pewne decyzje o tym, jakiego rodzaju inżynierię danych wykonać. Podejście KNN nie wymaga dalszych decyzji — ten sam kod, którego użyłem na przykładzie liniowym, może być ponownie użyty w całości na nowych danych, aby uzyskać wykonalny zestaw prognoz:

podobnie jak w przypadku przykładów klasyfikatorów, ustawienie wyższej wartości k pomaga nam uniknąć nadmiernego dopasowania, chociaż możesz zacząć tracić moc predykcyjną na marginesie, szczególnie na krawędziach zestawu danych. Rozważmy pierwszy przykładowy zestaw danych z przewidywaniami wykonanymi z k ustawionym na jeden, czyli podejście najbliższe sąsiadowi:

nasze prognozy przeskakują nieregularnie, gdy model przeskakuje z jednego punktu w zbiorze danych do następnego. Natomiast ustawienie k na 10, tak aby 10 punktów było uśrednionych razem dla przewidywania, daje znacznie płynniejszą jazdę:

ogólnie wygląda to lepiej, ale widać problem na krawędziach danych. Ponieważ nasz model bierze pod uwagę tak wiele punktów dla danej prognozy, kiedy zbliżymy się do jednej z krawędzi naszej próbki, nasze prognozy zaczynają się pogarszać. Możemy rozwiązać ten problem nieco ważąc nasze prognozy do bliższych punktów, choć wiąże się to z własnymi kompromisami.

jak

podczas konfigurowania modelu KNN jest tylko kilka parametrów, które należy wybrać/można zmodyfikować, aby poprawić wydajność.

K: Liczba sąsiadów: Jak wspomniano, zwiększenie K będzie miało tendencję do wygładzania granic decyzji, unikając nadmiernego dopasowania kosztem pewnej rozdzielczości. Nie ma jednej wartości K, która będzie działać dla każdego pojedynczego zbioru danych. W przypadku modeli klasyfikacyjnych, zwłaszcza jeśli istnieją tylko dwie klasy, zwykle wybiera się liczbę nieparzystą dla k. jest tak, że algorytm nigdy nie prowadzi do „remisu”: np. patrzy na najbliższe cztery punkty i stwierdza, że dwa z nich należą do kategorii niebieskiej, a dwa do kategorii czerwonej.

metryka odległości: Jak się okazuje, istnieją różne sposoby pomiaru tego, jak „blisko” są do siebie dwa punkty, a różnice między tymi metodami mogą stać się znaczące w wyższych wymiarach. Najczęściej używany jest dystans Euklidesowy, standardowy rodzaj, którego można było nauczyć się w gimnazjum za pomocą twierdzenia Pitagorasa. Inną metryką jest tak zwana „odległość Manhattanu”, która mierzy odległość pokonaną w każdym kierunku kardynalnym, a nie wzdłuż przekątnej (tak, jakbyś szedł z jednego skrzyżowania na Manhattanie i musiał podążać za siatką ulic, zamiast być w stanie jechać najkrótszą drogą „w linii prostej”). Ogólnie rzecz biorąc, są to właściwie obie formy tzw. „odległości Minkowskiego”, której wzór jest:

gdy p jest ustawione na 1, Ten wzór jest taki sam jak odległość Manhattana, a gdy jest ustawione na 2, odległość euklidesowa.

wagi: jednym ze sposobów rozwiązania zarówno problemu możliwego „remisu”, gdy algorytm głosuje na klasę, jak i problemu, w którym nasze prognozy regresji pogorszyły się w kierunku krawędzi zbioru danych, jest wprowadzenie ważenia. W przypadku wag punkty w pobliżu będą liczone więcej niż punkty dalej. Algorytm nadal będzie patrzył na wszystkich k najbliższych sąsiadów, ale bliżsi sąsiedzi będą mieli więcej głosów niż ci dalej. Nie jest to idealne rozwiązanie i stwarza możliwość ponownego przepełnienia. Rozważmy przykład regresji, tym razem z wagami:

nasze prognozy idą teraz do krawędzi zbioru danych, ale widać, że nasze prognozy są teraz znacznie bliżej poszczególnych punktów. Metoda ważona działa dość dobrze, gdy jesteś między punktami, ale gdy zbliżasz się do konkretnego punktu, wartość tego punktu ma coraz większy wpływ na przewidywanie algorytmu. Jeśli zbliżysz się wystarczająco blisko punktu, to prawie jak ustawienie k na jeden, ponieważ ten punkt ma tak duży wpływ.

skalowanie/normalizowanie: na koniec, ale co najważniejsze, chodzi o to, że modele KNN mogą zostać odrzucone, jeśli różne zmienne funkcji mają bardzo różne skale. Rozważ model, który próbuje przewidzieć, powiedzmy, cenę sprzedaży domu na rynku w oparciu o funkcje, takie jak liczba sypialni i całkowita powierzchnia domu itp. Istnieje więcej rozbieżności w liczbie stóp kwadratowych w domu niż w liczbie sypialni. Zazwyczaj domy mają tylko niewielką garść sypialni, a nawet największy dwór nie będzie miał dziesiątek lub setek sypialni. Z drugiej strony, stopy kwadratowe są stosunkowo małe, więc domy mogą wahać się od blisko, powiedzmy, 1000 metrów kwadratowych na małej stronie do dziesiątek tysięcy stóp kwadratowych na dużej stronie.

rozważmy porównanie domu o powierzchni 2000 m2 z 2 sypialniami i domu o powierzchni 2010 m2 z dwiema sypialniami — 10 m2. stopy prawie nie robią różnicy. Natomiast dom o powierzchni 2000 stóp kwadratowych z trzema sypialniami Jest bardzo inny i reprezentuje bardzo inny i prawdopodobnie bardziej ciasny układ. Naiwny komputer nie miałby jednak kontekstu, aby to zrozumieć. Powiedziałoby, że 3 sypialnia jest tylko „jedna” jednostka od 2 sypialni, podczas gdy 2,010 sq stopka jest „dziesięć” od 2,000 sq stopka. Aby tego uniknąć, dane funkcji powinny być skalowane przed wdrożeniem modelu KNN.

mocne i słabe strony

modele KNN są łatwe do wdrożenia i dobrze radzą sobie z nieliniowościami. Dopasowanie modelu jest również szybkie: komputer nie musi obliczać żadnych konkretnych parametrów ani wartości. Kompromis polega na tym, że podczas gdy model jest szybki w konfiguracji, jest wolniejszy w przewidywaniu, ponieważ aby przewidzieć wynik dla nowej wartości, będzie musiał przeszukać wszystkie punkty w swoim zestawie treningowym, aby znaleźć najbliższe. W przypadku dużych zbiorów danych KNN może być zatem stosunkowo powolną metodą w porównaniu z innymi regresjami, które mogą trwać dłużej, aby dopasować, ale następnie dokonać swoich prognoz przy stosunkowo prostych obliczeniach.

innym problemem z modelem KNN jest brak możliwości jego interpretacji. Regresja liniowa OLS będzie miała jasno interpretowalne współczynniki, które same mogą dać pewne wskazanie „wielkości efektu” danej cechy (chociaż należy zachować ostrożność przy przypisywaniu przyczynowości). Pytanie, które funkcje mają największy efekt, nie ma jednak sensu dla modelu KNN. Częściowo z tego powodu modele KNN nie mogą być tak naprawdę używane do wyboru funkcji, w sposób, w jaki może być regresja liniowa z dodatkowym terminem funkcji kosztowej, takim jak ridge lub lasso, lub sposób, w jaki drzewo decyzyjne domyślnie wybiera, które funkcje wydają się najbardziej wartościowe.