Statowarity oznacza, że właściwości statystyczne szeregu czasowego tj. średnia, wariancja i KOWARIANCJA nie zmieniają się w czasie. Wiele modeli statystycznych wymaga, aby serie były nieruchome, aby tworzyć skuteczne i precyzyjne prognozy.
do sprawdzenia stacjonarności szeregów czasowych posłużyły dwa testy statystyczne – rozszerzony test Dickeya Fullera („ADF”) i test Kwiatkowskiego-Phillipsa-Schmidta-Shina („KPSS”). Stosuje się również metodę przekształcania niestacjonarnych szeregów czasowych w szeregi stacjonarne.
ta pierwsza komórka importuje standardowe pakiety i ustawia wykresy, aby pojawiły się w linii.
:
%matplotlib inlineimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport statsmodels.api as sm
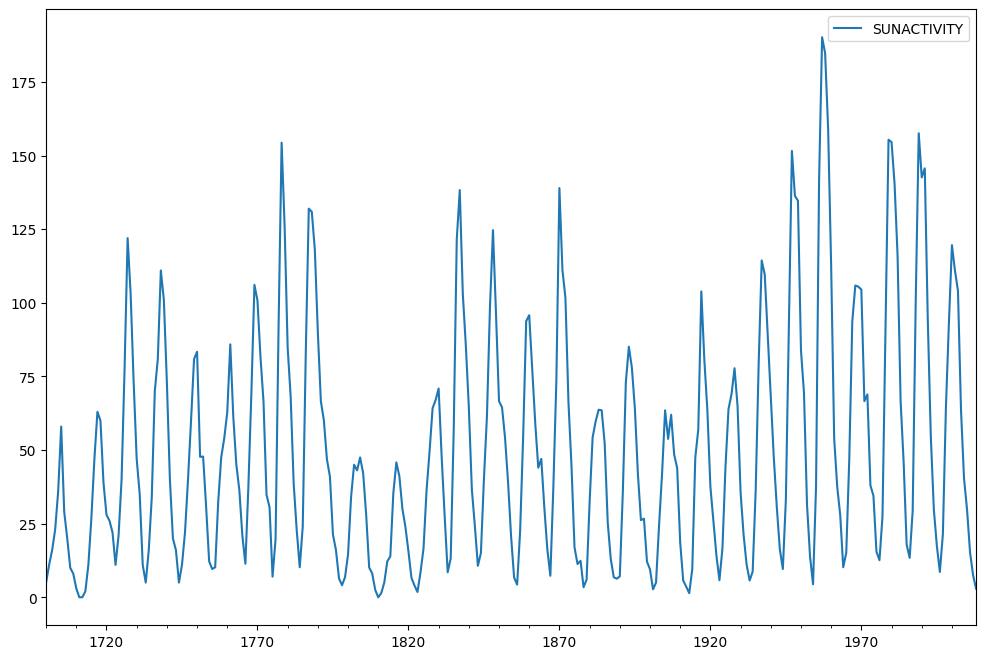
używany jest zbiór danych plam słonecznych. Zawiera on roczne (1700-2008) dane na temat plam słonecznych z National Geophysical Data Center.
:
sunspots = sm.datasets.sunspots.load_pandas().data
niektóre wstępne przetwarzanie odbywa się na danych. Kolumna ” rok ” służy do tworzenia indeksu.
:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))del sunspots
dane są już wykreślone.
:
sunspots.plot(figsize=(12,8))
:
<AxesSubplot:>
test ADF¶
test ADF jest używany do określenia obecności pierwiastka jednostkowego w serii, a zatem pomaga w zrozumieniu, czy seria jest stacjonarna, czy nie. Hipoteza zerowa i alternatywna tego testu to:
hipoteza zerowa: seria ma pierwiastek jednostkowy.
hipoteza Alternatywna: szereg nie ma pierwiastka jednostkowego.
jeśli hipoteza zerowa nie została odrzucona, test ten może dostarczyć dowodów, że seria jest niestacjonarna.
funkcja jest tworzona w celu przeprowadzenia testu ADF w szeregu czasowym.
:
from statsmodels.tsa.stattools import adfullerdef adf_test(timeseries): print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC') dfoutput = pd.Series(dftest, index=) for key,value in dftest.items(): dfoutput = value print (dfoutput)
test KPSS¶
KPSS jest kolejnym testem sprawdzającym stacjonarność szeregów czasowych. Hipoteza zerowa i alternatywna dla testu KPSS są przeciwne do testu ADF.
hipoteza zerowa: Proces jest tendencja stacjonarne.
hipoteza Alternatywna: szereg ma pierwiastek jednostkowy (szereg nie jest stacjonarny).
funkcja jest tworzona w celu przeprowadzenia testu KPSS w szeregu czasowym.
:
from statsmodels.tsa.stattools import kpssdef kpss_test(timeseries): print ('Results of KPSS Test:') kpsstest = kpss(timeseries, regression='c', nlags="auto") kpss_output = pd.Series(kpsstest, index=) for key,value in kpsstest.items(): kpss_output = value print (kpss_output)
testy ADF dają następujące wyniki-statystykę badania, wartość p i wartość krytyczną w przedziałach ufności 1%, 5% i 10%.
test ADF jest teraz stosowany na danych.
:
adf_test(sunspots)
Results of Dickey-Fuller Test:Test Statistic -2.837781p-value 0.053076#Lags Used 8.000000Number of Observations Used 300.000000Critical Value (1%) -3.452337Critical Value (5%) -2.871223Critical Value (10%) -2.571929dtype: float64
w oparciu o poziom istotności 0,05 i wartość P testu ADF, hipoteza zerowa nie może być odrzucona. Dlatego seria jest niestacjonarna.
testy KPSS dają następujące wyniki-statystykę badania, wartość p i wartość krytyczną w przedziałach ufności 1%, 5% i 10%.
test KPSS jest teraz stosowany na danych.
:
kpss_test(sunspots)
Results of KPSS Test:Test Statistic 0.669866p-value 0.016285Lags Used 7.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
w oparciu o poziom istotności 0,05 i wartość P testu KPSS, istnieją dowody na odrzucenie hipotezy zerowej na rzecz alternatywy. W związku z tym seria jest niestacjonarna zgodnie z testem KPSS.
zawsze lepiej zastosować oba testy, aby mieć pewność, że seria jest naprawdę nieruchoma. Możliwe wyniki zastosowania tych badań stacjonarnych są następujące:
tutaj, ze względu na różnicę w wynikach testu ADF i testu KPSS, można wywnioskować, że seria jest trendem stacjonarnym, a nie ścisłym stacjonarnym. Seria może być detrendowana przez różnicowanie lub dopasowanie modelu.
Detrending przez różnicowanie¶
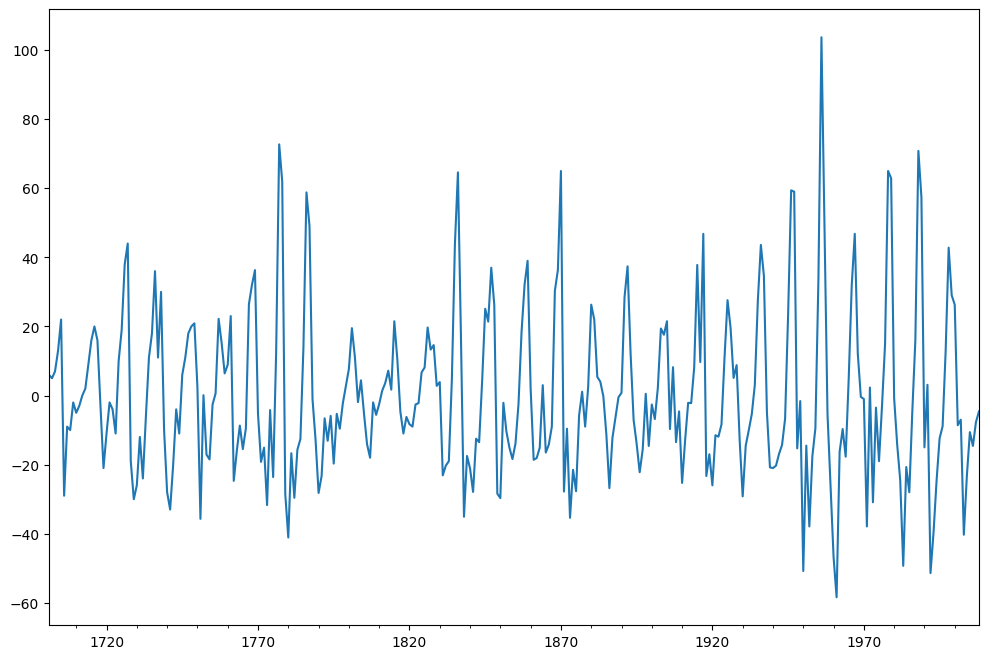
jest to jedna z najprostszych metod detrendingu szeregów czasowych. Konstruuje się nowy szereg, w którym wartość w bieżącym kroku czasowym jest obliczana jako różnica między pierwotną obserwacją a obserwacją w poprzednim kroku czasowym.
różnicowanie jest stosowane na danych i wynik jest wykreślany.
:
sunspots = sunspots - sunspots.shift(1)sunspots.dropna().plot(figsize=(12,8))
:
<AxesSubplot:>
test ADF jest teraz stosowany na tych detrendowanych wartościach i sprawdzana jest stacjonarność.
:
adf_test(sunspots.dropna())
Results of Dickey-Fuller Test:Test Statistic -1.486166e+01p-value 1.715552e-27#Lags Used 7.000000e+00Number of Observations Used 3.000000e+02Critical Value (1%) -3.452337e+00Critical Value (5%) -2.871223e+00Critical Value (10%) -2.571929e+00dtype: float64
w oparciu o wartość P testu ADF, istnieją dowody na odrzucenie hipotezy zerowej na rzecz alternatywy. Dlatego seria jest teraz ściśle stacjonarna.
test KPSS jest teraz stosowany na tych detrendowanych wartościach i sprawdzana jest stacjonarność.
:
kpss_test(sunspots.dropna())
Results of KPSS Test:Test Statistic 0.021193p-value 0.100000Lags Used 0.000000Critical Value (10%) 0.347000Critical Value (5%) 0.463000Critical Value (2.5%) 0.574000Critical Value (1%) 0.739000dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/stattools.py:1911: InterpolationWarning: The test statistic is outside of the range of p-values available in thelook-up table. The actual p-value is greater than the p-value returned. warn_msg.format(direction="greater"), InterpolationWarning
w oparciu o wartość P testu KPSS, hipoteza zerowa nie może zostać odrzucona. Dlatego seria jest stacjonarna.
wnioski¶
stosowane są dwa testy sprawdzające stacjonarność szeregu czasowego, mianowicie test ADF i test KPSS. Detrending odbywa się za pomocą różnicowania. Trend stacjonarne szeregi czasowe są przekształcane w ścisłe stacjonarne szeregi czasowe. Wymagany model prognozowania można teraz zastosować na stacjonarnych danych szeregów czasowych.