grunderna: KNN för klassificering och regression

datavetenskap från grunden

datavetenskap eller tillämpad statistik kurser börjar vanligtvis med linjära modeller, men i sin väg är K-närmaste grannar förmodligen den enklaste allmänt använda modellen konceptuellt. KNN-modeller är egentligen bara tekniska implementeringar av en gemensam intuition, att saker som delar liknande funktioner tenderar att vara, ja, liknande. Detta är knappast en djup insikt, men dessa praktiska implementeringar kan vara extremt kraftfulla och, avgörande för någon som närmar sig en okänd dataset, kan hantera icke-linjäriteter utan komplicerad datateknik eller modelluppsättning.

vad

som ett illustrativt exempel, låt oss betrakta det enklaste fallet med att använda en KNN-modell som klassificerare. Låt oss säga att du har datapunkter som faller i en av tre klasser. Ett tvådimensionellt exempel kan se ut så här:

du kan förmodligen se ganska tydligt att de olika klasserna är grupperade ihop — det övre vänstra hörnet av graferna verkar tillhöra den orange klassen, den högra/mellersta delen till den blå klassen. Om du fick koordinaterna för ny punkt någonstans i diagrammet och frågade vilken klass det troligen skulle tillhöra, skulle svaret oftast vara ganska tydligt. Varje punkt i det övre vänstra hörnet av diagrammet kommer sannolikt att vara orange, etc.

uppgiften blir lite mindre säker mellan klasserna, men där vi måste lösa oss på en beslutsgräns. Tänk på den nya punkten som läggs till i rött nedan:

ska denna nya punkt klassificeras som orange eller blå? Poängen verkar falla mellan de två klusterna. Din första intuition kan vara att välja det kluster som ligger närmare den nya punkten. Detta skulle vara den ’närmaste granne’ tillvägagångssätt, och trots att konceptuellt enkel, det ger ofta ganska förnuftiga förutsägelser. Vilken tidigare identifierad punkt är den nya punkten närmast? Det kanske inte är uppenbart att bara eyeballing grafen vad svaret är, men det är lätt för datorn att springa igenom punkterna och ge oss ett svar:

det ser ut som den närmaste punkten är i den blå kategorin, så vår nya punkt är förmodligen också. Det är den närmaste grannmetoden.

vid denna tidpunkt kanske du undrar vad ’k’ i k-närmaste grannar är för. K är antalet närliggande punkter som modellen kommer att titta på när man utvärderar en ny punkt. I vårt enklaste närmaste grannexempel var detta värde för k helt enkelt 1-Vi tittade på närmaste granne och det var det. Du kunde dock ha valt att titta på närmaste 2 eller 3 poäng. Varför är detta viktigt och varför skulle någon ställa k på ett högre antal? För en sak, gränserna mellan klasserna kan stöta upp bredvid varandra på ett sätt som gör det mindre uppenbart att den närmaste punkten kommer att ge oss rätt klassificering. Tänk på de blå och gröna regionerna i vårt exempel. Låt oss faktiskt zooma in på dem:

Lägg märke till att medan de övergripande regionerna verkar distinkta nog, verkar deras gränser vara lite sammanflätade med varandra. Detta är ett vanligt inslag i datamängder med lite brus. När så är fallet blir det svårare att klassificera saker i gränsområdena. Tänk på denna nya punkt:

å ena sidan ser det visuellt ut som att den närmaste tidigare identifierade punkten är blå, vilket vår dator enkelt kan bekräfta för oss:

å andra sidan verkar den närmaste blå punkten som en bit av en outlier själv, långt ifrån centrum av den blå regionen och typ av omgiven av gröna punkter. Och den här nya punkten är till och med på utsidan av den blå punkten! Vad händer om vi tittade på de tre närmaste punkterna till den nya röda punkten?

eller till och med de närmaste fem punkterna till den nya punkten?

nu verkar det som om vår nya punkt ligger i ett grönt grannskap! Det råkade ha en närliggande blå punkt, men övervägande eller närliggande punkter är gröna. I det här fallet kanske det är vettigt att ställa in ett högre värde för k, att titta på en handfull närliggande punkter och få dem att rösta på något sätt på förutsägelsen för den nya punkten.

problemet som illustreras är överpassande. När k är inställd på en, gränsen mellan vilka regioner identifieras av algoritmen som blå och grön är ojämn, den ormar tillbaka med varje enskild punkt. Den röda punkten ser ut som om den kan vara i den blå regionen:

vilket ger k upp till 5 jämnar emellertid ut beslutsgränsen när de olika närliggande punkterna röstar. Den röda punkten verkar nu fast i det gröna grannskapet:

avvägningen med högre värden på k är förlusten av granularitet i beslutsgränsen. Inställning k mycket hög tenderar att ge dig jämna gränser, men den verkliga världen gränser du försöker modellera kanske inte är helt slät.

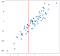
praktiskt taget kan vi använda samma typ av närmaste granners tillvägagångssätt för regressioner, där vi vill ha ett individuellt värde snarare än en klassificering. Tänk på följande regression nedan:

data genererades slumpmässigt, men genererades för att vara linjär, så en linjär regressionsmodell skulle naturligtvis passa dessa data Bra. Jag vill dock påpeka att du kan approximera resultaten av den linjära metoden på ett konceptuellt enklare sätt med en k-närmaste grannar. Vår ’regression’ i det här fallet kommer inte att vara en enda formel som en OLS-modell skulle ge oss, utan snarare ett bäst förutsagt utgångsvärde för en given ingång. Tänk på värdet av -.75 på X-axeln, som jag har markerat med en vertikal linje:

utan att lösa några ekvationer kan vi komma till en rimlig approximation av vad utgången ska vara bara genom att överväga de närliggande punkterna:

det är vettigt att det förutsagda värdet ska vara nära dessa punkter, inte mycket lägre eller högre. Kanske en bra förutsägelse skulle vara genomsnittet av dessa punkter:

du kan tänka dig att göra detta för alla möjliga ingångsvärden och komma med förutsägelser överallt:

att ansluta alla dessa förutsägelser med en linje ger oss vår regression:

i det här fallet är resultaten inte en ren linje, men de spårar dataens uppåtgående lutning ganska bra. Detta kanske inte verkar fruktansvärt imponerande, men en fördel med enkelheten i denna implementering är att den hanterar icke-linjäritet väl. Tänk på den här nya samlingen av poäng:

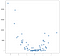
dessa punkter genererades genom att helt enkelt kvadrera värdena från föregående exempel, men antar att du kom över en datauppsättning som denna i naturen. Det är uppenbarligen inte linjärt och medan en OLS-stilmodell enkelt kan hantera denna typ av data, kräver det användning av icke-linjära eller interaktionsvillkor, vilket innebär att datavetenskaparen måste fatta några beslut om vilken typ av datateknik som ska utföras. KNN-metoden kräver inga ytterligare beslut – samma kod som jag använde på det linjära exemplet kan återanvändas helt på de nya uppgifterna för att ge en fungerande uppsättning förutsägelser:

som med klassificeringsexemplen hjälper inställningen av ett högre värde k oss att undvika överfit, men du kan börja förlora prediktiv kraft på marginalen, särskilt runt kanterna på din datamängd. Tänk på det första exempeldatasetet med förutsägelser gjorda med k inställd på en, Det är en närmaste grannstrategi:

våra förutsägelser hoppar oregelbundet när modellen hoppar från en punkt i datasetet till nästa. Däremot, inställning k vid tio, så att tio totala poäng är i genomsnitt tillsammans för förutsägelse ger en mycket smidigare åktur:

generellt ser det bättre ut, men du kan se något av ett problem vid kanterna av data. Eftersom vår modell tar så många poäng i beaktande för en viss förutsägelse, när vi kommer närmare en av kanterna i vårt prov, börjar våra förutsägelser bli värre. Vi kan ta itu med denna fråga något genom att väga våra förutsägelser till närmare punkter, även om detta kommer med sina egna kompromisser.

hur

när du ställer in en KNN-modell finns det bara en handfull parametrar som måste väljas/kan justeras för att förbättra prestanda.

K: antalet grannar: Som diskuterats tenderar ökande K att jämna ut beslutsgränser och undvika överfit på bekostnad av viss upplösning. Det finns inget enskilt värde på k som fungerar för varje dataset. För klassificeringsmodeller, särskilt om det bara finns två klasser, väljs vanligtvis ett udda tal för k. Det är så att algoritmen aldrig går in i en ’slips’: t.ex. tittar den på de närmaste fyra punkterna och finner att två av dem är i den blå kategorin och två är i den röda kategorin.

Avståndsmätvärde: Det finns, som det visar sig, olika sätt att mäta hur ’nära’ två punkter är till varandra, och skillnaderna mellan dessa metoder kan bli betydande i högre dimensioner. Det vanligaste är euklidiskt avstånd, den standardtyp du kanske har lärt dig i gymnasiet med hjälp av Pythagoras sats. Ett annat mått är så kallat ’Manhattan distance’, som mäter avståndet i varje kardinalriktning snarare än längs diagonalen (som om du gick från en gatukorsning på Manhattan till en annan och var tvungen att följa gatunätet snarare än att kunna ta den kortaste ’som fågelvägen’). Mer allmänt är dessa faktiskt båda formerna av det som kallas ’Minkowski-avstånd’, vars formel är:

när p är inställd på 1 är denna formel densamma som Manhattan-avståndet, och när den är inställd på två, euklidiskt avstånd.

vikter: ett sätt att lösa både frågan om ett eventuellt slips när algoritmen röstar på en klass och frågan där våra regressionsprognoser blev värre mot kanterna på datasetet är genom att införa viktning. Med vikter räknas de närmaste poängen mer än poängen längre bort. Algoritmen kommer fortfarande att titta på alla k närmaste grannar, men närmare grannar kommer att ha mer av en röst än de längre bort. Detta är inte en perfekt lösning och ger möjlighet till överfitting igen. Tänk på vårt regressionsexempel, den här gången med vikter:

våra förutsägelser går direkt till kanten av datasatsen nu, men du kan se att våra förutsägelser nu svänger mycket närmare de enskilda punkterna. Den viktade metoden fungerar ganska bra när du är mellan punkter, men när du kommer närmare och närmare en viss punkt har den punktens värde mer och mer inflytande på algoritmens förutsägelse. Om du kommer tillräckligt nära en punkt är det nästan som att ställa k till en, eftersom den punkten har så mycket inflytande.

skalning/normalisering: en sista men avgörande punkt är att KNN-modeller kan kastas om olika funktionsvariabler har mycket olika skalor. Tänk på en modell som försöker förutsäga, säg försäljningspriset för ett hus på marknaden baserat på funktioner som antalet sovrum och husets totala kvadratmeter etc. Det finns mer variation i antalet kvadratmeter i ett hus än det finns i antalet sovrum. Vanligtvis har hus bara en liten handfull sovrum, och inte ens den största herrgården kommer att ha tiotals eller hundratals sovrum. Kvadratfot, å andra sidan, är relativt små, så hus kan variera från nära, säg, 1000 kvm bedrift på den lilla sidan till tiotusentals kvm fötter på den stora sidan.

Tänk på jämförelsen mellan ett 2000 kvm fothus med 2 sovrum och ett 2010 kvm fothus med två sovrum — 10 kvm. fötter gör knappast någon skillnad. Däremot är ett 2000 kvm fothus med tre sovrum väldigt annorlunda och representerar en mycket annorlunda och eventuellt mer trång layout. En naiv dator skulle dock inte ha sammanhanget att förstå det. Det skulle säga att 3-sovrummet bara är en enhet bort från 2-sovrummet, medan 2,010 sq-sidfoten är ’tio’ bort från 2,000 sq-sidfoten. För att undvika detta bör funktionsdata skalas innan en KNN-modell implementeras.

styrkor och svagheter

KNN-modeller är lätta att implementera och hantera icke-linjäriteter väl. Montering av modellen tenderar också att vara snabb: datorn behöver trots allt inte beräkna några speciella parametrar eller värden. Avvägningen här är att medan modellen är snabb att ställa in, är den långsammare att förutsäga, eftersom den för att förutsäga ett resultat för ett nytt värde måste söka igenom alla punkter i sin träningsuppsättning för att hitta de närmaste. För stora datamängder kan KNN därför vara en relativt långsam metod jämfört med andra regressioner som kan ta längre tid att passa men sedan göra sina förutsägelser med relativt enkla beräkningar.

en annan fråga med en KNN-modell är att den saknar tolkningsförmåga. En OLS linjär regression kommer att ha tydligt tolkbara koefficienter som själva kan ge en viss indikation på ’effektstorleken’ för en given funktion (även om viss försiktighet måste vidtas vid tilldelning av kausalitet). Att fråga vilka funktioner som har störst effekt är dock inte meningsfullt för en KNN-modell. Delvis på grund av detta kan KNN-modeller inte riktigt användas för funktions val, på det sätt som en linjär regression med en extra kostnad funktion term, som ridge eller lasso, kan vara, eller det sätt som ett beslutsträd implicit väljer vilka funktioner verkar mest värdefulla.