Kunskapsstruktur

extraherat från ett häfte som åtföljer en workshop för gymnasielärare.

av Robert J. Dufresne, William J. Leonard och William J. Gerace

vår grupp på UMass har utvecklat en kognitiv modell som hjälper oss att representera skillnaderna i hur experter och nybörjare lagrar och använder innehållskunskap. Modellen hjälper oss också att rikta in oss på specifika områden som nybörjare måste koncentrera sig på för att bli bättre problemlösare. Modellen är dock bara en representation av kunskapsstrukturen, och den utvecklas ständigt. Således får det inte tas för bokstavligt. Dess användbarhet kommer från dess förmåga att ge en konkret manifestation, dock ofullkomlig, av hur experter och nybörjare tänker. Modellen hjälper oss att diskutera:

1. lagring av domänspecifik kunskap;
2. expert – och nybörjarliknande problemlösningsbeteende;
3. den hierarkiska strukturen i en experts kunskapsbutik;
4. missuppfattningar;
5. effekterna av målfria och målstyrda frågor; och
6. metakommunikationsprocessen.

i denna workshop—och i vår inställning till fysik i allmänhet – – – det finns 3 grundläggande teman:

1. särskilda typer av kunskap och kunskapsstrukturer behövs för skicklig problemlösning. Mycket av denna kunskap är konceptuell till sin natur, i motsats till operativa eller processuella, och kraftfulla kunskapsstrukturer involverar nödvändigtvis konceptuella element. Förekomsten av konceptuella element i kunskapsstrukturerna är nyckeln till att ha en ”djupare förståelse” av fysiken.
2. särskilda typer av kognitiva processer krävs för förvärv av konceptuell kunskap och konstruktion av användbara kunskapsstrukturer.
3. det är möjligt att utforma aktiviteter som främjar dessa önskvärda kognitiva processer. I många fall är dessa aktiviteter helt enkelt aktualiseringar av de kognitiva processerna själva. (Denna punkt kommer förhoppningsvis att bli tydligare senare.)

vi kommer att utarbeta vart och ett av dessa teman innan vi fokuserar på specifika exempel.

tema 1: Vad behöver eleverna veta och hur ska det de vet vara strukturerat för effektiv problemlösning?

vi börjar med att identifiera några av de olika typerna av kunskap som eleverna behöver veta:

• konceptuell kunskap, såsom begreppet momentum eller energi, eller att ett objekts hastighet förändras när det accelererar, eller att ett objekts gravitationspotential energi minskar när det faller.
• faktakunskap, såsom värdet av gravitationskonstanten g, månens radie eller järnens densitet.
• representativ kunskap, till exempel hur man ritar och använder grafer.
• strategisk kunskap, såsom förmågan att känna igen tillämpligheten av ett koncept, såsom momentum bevaras när det inte finns några yttre krafter, eller att energi bevaras när det inte finns några icke-konservativa krafter.
• metakognitiv kunskap, till exempel medvetenheten om underliggande antaganden, eller att ett svar bör kontrolleras genom att lösa problemet på ett annat sätt.
• självkännedom, som att känna till sina troliga källor till misstag, eller veta att man borde vara mer procedurell när man löser problem.
• operativ kunskap, till exempel hur man tar korsprodukten eller punktprodukten av två vektorer, eller hur man tar determinanten av en matris, eller hur man ritar ett fritt kroppsdiagram.
• Procedurkunskap, till exempel när man ska använda energibesparing (dvs. när man ska ange ett koordinatsystem (t.ex. när man hittar potentiell energi), eller när man ska rita ett frikroppsdiagram (t. ex. vid tillämpning av Newtons lagar).
• Problem – tillståndskunskap, som är funktionerna i ett problem som används för att bestämma hur man löser det. Exempel är: att veta att det inte finns några yttre krafter i ett visst problem, eller att det inte finns några icke-konservativa krafter i problemet, eller att ett objekt är i vila initialt, eller att objektet är i en lutning.

dessa typer av kunskap måste organiseras och struktureras för effektiv användning vid problemlösning. För att diskutera de organisatoriska och strukturella aspekterna av kunskap har vi funnit det bekvämt att i stor utsträckning klassificera dessa typer i tre allmänna kategorier. Vi kallar dessa tre grupper: konceptuell kunskap, operativ och Procedurkunskap och Problemstatskunskap. I Fig. 1, Dessa tre allmänna kategorier visas i en representation av hur experter lagrar innehållskunskap.

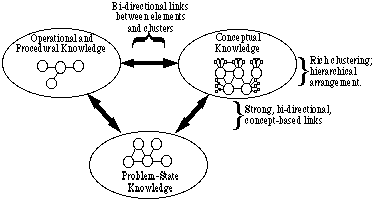Fig. 1: En representation av en experts kunskapsstruktur

experten har en rik gruppering av begrepp, där varje koncept är relaterat till många andra begrepp, och relationerna mellan begrepp är tydligt förstådda. Begrepp ordnas hierarkiskt med paraplykoncept för att närmare relatera dem. Faktum är att paraplykoncept används för att gruppera element inom var och en av de tre kategorierna. Experten har en stor butik med problemstatlig kunskap, inklusive mycket information om vilka principer som gäller för vissa situationer. Experten har också en stor butik med ekvationer, operationer och procedurer (EOPs) som snabbt kan nås.

länkarna mellan varje par av kategorier är mycket starka: problemtillstånd är starkt kopplade till begrepp och till EOPs, som själva är starkt kopplade till varandra. Samma paraplybegrepp används för att gruppera begrepp, problemtillstånd och EOPs. Därför kan begrepp för ett visst problem användas för att bestämma lämpligheten och tillämpligheten av ekvationer och nyttan av specifika operationer och procedurer.

(man måste vara mycket försiktig här för att inte vara för stel i sitt tänkande, för det är lätt att vara oense om vilken av dessa kategorier som ska användas för att klassificera ett visst kunskapselement, eller om det bara hör till en kategori. Vårt syfte är helt enkelt att ha en mekanism för att visualisera de flera associeringsnivåer som kan uppstå mellan element.)

vi brukar använda termen länkning för att betyda en formad koppling mellan två element av samma eller olika kunskapstyper, och termen clustering för att hänvisa till föreningar mellan flera element eller kluster. Vad som gör denna typ av diskussion mycket svårt är att det finns en slags iterativ process som pågår här: Ett mycket starkt band mellan tre punkter—ett konceptuellt kluster, erkännandet av de omständigheter som gör konceptet tillämpligt och de förfaranden som behövs för att tillämpa konceptet – – – bildar en ny typ av kunskapselement som vi lägger in i strategisk kunskap (en fjärde kategori). Detta nya kunskapselement är vad vissa kallar ett schema och involverar ofta också problemstatskunskap. Eftersom kunskapselementet är konceptuellt i naturen replikeras det (dvs upprepas) i den konceptuella bubblan.

om vi tittar närmare på den konceptuella bubblan ser vi några av de specifika typerna av konceptuell kunskap, till exempel Representationskunskap, strategisk kunskap, metakognitiv kunskap och kunskap om grundläggande begrepp. Detta representeras i Fig. 2. (Andra typer av konceptuell kunskap visas inte.)

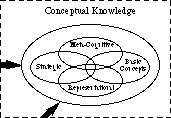Fig. 2: typer av konceptuell kunskap

hur skiljer sig en nybörjares kunskapsstruktur från en experts? Som representeras i Fig. 3, nybörjare har i allmänhet en dålig gruppering av begrepp. Många länkar är olämpliga; andra är obefintliga. Några av de olämpliga länkarna är extremt starka, vilket leder till missuppfattningar. Nybörjare använder i allmänhet inte paraplykoncept för att gruppera element. De har en liten butik av problemsituationer, där ytfunktioner används för att klustera dem tillsammans och bestämma hur problem ska lösas. De känner till ett relativt stort antal ekvationer, men de kommer ofta ihåg dem felaktigt eller behöver leta upp dem för att kunna använda dem. De har lärt sig operationer och förfaranden, men de är ännu inte skickliga på dem. Därför kan det inte sägas att de ”känner” dem.

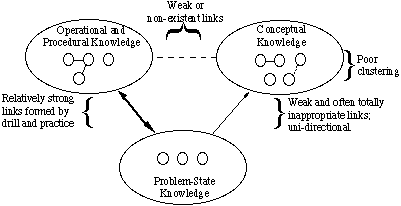Fig. 3: en representation av nybörjarens kunskapsstruktur

länkar mellan begrepp och EOPs är svaga eller obefintliga. Kopplingar mellan begrepp och problemsituationer är också svaga. Således kan en nybörjare inte analysera ett problem och kan inte bestämma lämpligheten för vissa ekvationer. Kopplingarna mellan problemsituationer och EOPs är relativt starka, men länkarna baseras främst på de kvantiteter som ekvationerna har gemensamt med de givna och uttryckliga okända problemen.

tema 2: I vilka typer av kognitiva processer måste eleverna engagera sig för att utveckla lämpliga kunskapsstrukturer?

för att svara på denna fråga måste vi först förstå hur experter och nybörjare löser problem annorlunda.

nybörjare misslyckas i allmänhet när de försöker lösa typiska problem i fysiken. Använda modellen för att representera processen, hur löser en typisk nybörjare ett problem? Eftersom de starkaste länkarna i nybörjarens kunskapsstruktur är mellan problemsituationer och ekvationer, föreslår läsning av ett problem omedelbart ekvationer som involverar de kvantiteter (kända och okända) som uttryckligen anges i problemet. Utan att bestämma tillämpligheten av dessa ekvationer, och utan att försöka tänka på andra ekvationer som kan innebära samma kvantiteter, börjar nybörjaren vanligtvis att manipulera de mest kända ekvationerna tills det okända kan lösas för. Den senaste ekvationen som behandlas i klassen är den mest lättillgängliga och den snabbast återkallade. Således letar nybörjaren efter och (om ”framgångsrik”) hittar bara ett sätt att lösa ett problem och slutar vanligtvis utan att undersöka andra möjligheter och utan att analysera problemsituationen. Ekvationerna som hittas på detta sätt är ofta olämpliga eftersom nybörjare ofta inte använder begrepp för att motivera deras tillämpning. Även om eleverna drivs att åberopa begrepp genom att analysera problem i förväg, är deras länkar till EOPs i allmänhet för svaga för att vara användbara för problemlösning. Kopplingar mellan begrepp och problemssituationer är också riktade, så analogier är inte särskilt användbara: Nybörjare kan inte använda analogier för att lösa problem eftersom de inte kan identifiera vilka av de problem de redan har löst är konceptuellt liknar den som de för närvarande försöker lösa. Istället använder nybörjare ytfunktioner för att skapa ”likhet” och försöka lösa nya problem baserat på deras likhet med ytfunktionerna i problem som de redan har löst.

eftersom experter klassificerar problem och EOPs enligt samma paraplybegrepp kan de ofta gå direkt från problemsituationer till lämpliga ekvationer, operationer och/eller procedurer. Eftersom kopplingarna mellan olika kategorier är starka kan svåra problem (sådana för vilka en direkt koppling mellan problemtillstånd och EOP ännu inte existerar) lösas genom att medvetet åberopa begrepp och därmed indirekt koppla problemtillstånd till lämpliga EOP(er). Eftersom kopplingarna mellan begrepp och problemsituationer är dubbelriktade är analogier ett extremt användbart problemlösningsverktyg för experter. Slutligen har experter vanligtvis mer än ett sätt att lösa ett visst problem.

här är en sammanfattning av de stora skillnaderna mellan experter och nybörjare:

1. nybörjare har en dålig gruppering av begrepp, vilket ofta leder till missuppfattningar. Experter har ett rikt kluster av begrepp, problemsituationer, ekvationer, procedurer och operationer, vilket leder till förbättrad problemlösningsförmåga.
2. nybörjare har vanligtvis bara ett sätt att lösa ett visst problem, medan experter ofta kan hitta mer än ett sätt. Därför kan experten försöka lösa inkonsekvenser när de inträffar och kontrollera svar, medan nybörjare inte är medvetna om att inkonsekvenser finns och inte kan kontrollera deras svar.
3. nybörjare använder ofta ekvationsmanipulation och använder sällan konceptbaserade strategier för att få svar. Experten använder begrepp och analogier för att föreslå flera lösningsmetoder och planerar en strategi för att hitta rätt svar.
4. nybörjare misslyckas ofta med att få rätt svar, och när de får rätt svar kan det lätt vara av fel anledning. När nybörjaren får rätt svar av fel anledning förstärks missuppfattningar och blir ännu svårare att övervinna. En expert får vanligtvis rätt svar och kan förklara varför svaret är korrekt.

det finns en mängd olika kognitiva processer som är fördelaktiga för att hjälpa nybörjare att utveckla en konceptbaserad problemlösningsmetod, som vi delar in i tre kategorier: analysprocesser, Resonemangsprocesser och metakognitiva processer.

analysprocesser

• problemanalys, såsom att konstruera en problemrepresentation.
• konceptuell analys, som att använda begrepp för att bestämma det kvalitativa beteendet hos fysiska objekt eller för att bilda en strategi.
• strategisk analys, såsom att identifiera och motivera fysikprinciper som är relevanta för en problemsituation.
• Representationsanalys, såsom att utforska olika representationer av ett problem.
• komplex konstruktiv analys, såsom att sönderdela en komplex situation till enklare.

Resonemangsprocesser

• jämföra och kontrastera, till exempel att identifiera hur objekt, situationer eller förhållanden är likartade och/eller olika.
• Tolkning, till exempel med hjälp av formen av en plot av position vs. tid att uppskatta objektets acceleration.
• speciella och begränsande fall, det vill säga utforska extrema och / eller kända förhållanden.
• prototyp och motexempel, till exempel generera arketypiska kategorier.
• generalisering, det vill säga erkänna de framträdande dragen i en omständighet eller situation.

Meta-kognitiva processer

• reflektion, det vill säga självstyrd granskning av syfte, mål, effekter av erfarenhet etc.
• Meta-kommunikation, som är medvetet deltagande i att upprätta och förfina kommunikationslinjer med läraren och andra studenter, och för att bestämma målen för lärande.
• självutvärdering, som att utvärdera sin prestation eller identifiera orsaker till att svårigheter uppstod när man löste ett problem.

dessa och andra processer uppmuntras av våra läroplaner. De specifika typerna av aktiviteter för att göra detta presenteras i nästa avsnitt.

Tema 3: Vilka typer av inlärningsaktiviteter eller erfarenheter främjar dessa fördelaktiga kognitiva processer?

följande aktiviteter kan användas av lärare för att stimulera de kognitiva processer som behövs för att utveckla en konceptuell förståelse för fysik:

1. använd flera representationer. En representation kan vara språklig, abstrakt, symbolisk, bildlig eller konkret. Genom att använda många olika representationer för samma kunskap, och låta eleverna översätta mellan representationer, hjälper studenten att interrelatera kunskapstyper och relatera kunskapen till fysisk erfarenhet. Det uppmuntrar bildandet av länkar mellan kunskapselement och främjar en rik kunskapsklustring.
2. gör framåt och bakåt referenser. Begrepp kräver lång tid att bildas. Således kan du inte vänta på att eleverna helt lär sig ett ämne innan de går vidare till nästa. Genom att göra framåtreferenser förbereder du studenten för nytt material. Genom att göra bakåtreferenser associerar du nytt material med etablerat (eller delvis etablerat) material, vilket gör kunskap sammanvävd och sammankopplad, snarare än linjär.
3. utforska utökade sammanhang. Begrepp kan vara extremt kontextberoende och blir inte globalt användbara förrän de är abstraherade. Att undersöka ett brett sammanhang av tillämplighet hjälper studenten att förfina och abstrakta begrepp. Det undviker också felaktiga eller förenklade generaliseringar.
4. Jämför och kontrast. Avgörande för processen att strukturera (eller omstrukturera) kunskap är klassificeringen och förhållandet mellan kunskapselement. Jämförelser och kontraster sensibiliserar eleverna för kategorier och relationer och hjälper eleverna att uppfatta de gemensamma drag och skillnader som behövs för att organisera sin kunskapsbutik.
5. kategorisera och klassificera. Parallellt med jämförelser och kontraster måste eleverna vara medvetna om kategorier och klassificeringssystem. Eleverna måste också öva på att skapa och känna igen kategoriseringssystem. Genom att kräva att eleverna klassificerar objekt, väljer namn för sina kategorier och förklarar sitt system kan vi hjälpa eleverna att strukturera om sin kunskapsbutik.
6. förutsäga & Visa (otillräcklighet av gammal modell). Noggrant utvalda demonstrationer och experiment kan användas för att få fram inkonsekvenser i studentmodeller. Eleverna ska visas en set-up eller experimentell apparat och bör uppmanas att förutsäga vad som kommer att hända när något görs. Det är viktigt att eleverna gör förutsägelser i förväg, vilket gör dem medvetna om sin egen modell. Eleverna kommer att överväga alternativa föreställningar endast om deras egna misslyckas. Att kräva att eleverna använder sina modeller och visar dem hur deras modeller är inkonsekventa eller otillräckliga kommer att förbereda dem för att skapa bättre (men fortfarande sina egna) modeller.

7. förklara (sammanfatta, beskriva, diskutera, definiera, etc.). Standardproblem berättar sällan läraren vad eleverna inte förstår. Även när eleverna får ett problem rätt kan det fortfarande vara förvirring om tillämpligheten av de använda ekvationerna. Att kräva att eleverna förklarar hur de kommer att lösa ett problem avslöjar missförstånd och missuppfattningar och hjälper eleverna att omorganisera sin kunskapsbutik. Dessutom ser eleverna sällan i standarddemonstrationer och experiment vad experter ser. Eleverna ska förklara och diskutera vad de tror att de har sett (under Predict & Show, till exempel), så att läraren kan interagera med elevernas modeller. Dessutom processen att förklara (eller sammanfatta, beskriva, diskutera etc.) hjälper eleverna att bli medvetna om sina egna modeller såväl som andra elevers modeller.

8. generera flera lösningar. Effektiv problemlösning kan inte ske om inte eleverna väljer från en uppsättning giltiga lösningsvägar. Genom att lösa problem på mer än ett sätt lär eleverna att prioritera delar av sin strategiska kunskap.

9. planera, motivera och strategisera. Mycket få relationer i fysiken är alltid giltiga. För att undvika ekvationsmanipulation bör eleverna uppmanas att planera (och sedan förklara) hur de kommer att lösa problem. Eleverna måste lära sig att bestämma vilka begrepp som är relevanta (och vilka är irrelevanta) för en viss problemsituation och hur man implementerar relevanta begrepp för att lösa det problemet. Att låta eleverna skapa sina egna strategier hjälper dem att lära sig hur begrepp används för att lösa problem.
10. reflektera (utvärdera, integrera, utöka, generalisera, etc.) Efter att ha avslutat de flesta aktiviteter drar eleverna nytta av att se tillbaka på vad de har gjort. Vilka mönster har de uppfattat? Vilka allmänna regler kan byggas? Andra typer av aktiviteter ger eleverna de bitar som behövs för att skapa en sammanhängande bild av fysiken, men någon form av reflekterande aktivitet behövs vanligtvis för att ”sätta ihop bitarna”.
11. meta-kommunicera om inlärningsprocessen. För att lära sig fysik (eller något annat komplext ämne) måste eleverna bli självinvesterade. De måste utsättas för andras (lärares och elevers) modeller. De måste varnas för att precision i kommunikationen är nödvändig; de måste informeras om vanliga fallgropar och feltolkningar; och de måste få veta att de bör strukturera om sin kunskap. Eleverna måste lära sig hur de lär sig bäst.