kinetisk energi är rörelsens energi. Ett uttryck för kinetisk energi härleds genom att titta på fallet med ett objekt som lyfts till en viss relativ höjd (sålunda görs arbete på detta objekt) och får sedan falla.
nyckelbegrepp
O kinetisk energi
mål
O härleda ett uttryck för kinetisk energi från fysikbegreppet arbete
O förstå förhållandet mellan arbete och kinetisk energi
O beräkna den kinetiska energin hos olika objekt
Låt oss börja!
relaterat arbete och kinetisk energi
i viss mening är arbete den mängd energi som läggs i en uppgift (eller kanske ”sätta i objektet”). Tänk dig till exempel att vi tar upp något föremål från golvet och höjer det till en viss höjd; vi har gjort en viss mängd arbete på det objektet. Om vi släpper det, accelererar det emellertid, som om det arbete vi gjorde för att lyfta föremålet förvandlas till rörelse. Genom detta exempel kan vi härleda en definition för kinetisk energi, som är rörelseenergi. Denna definition, som vi kommer att se, är nära relaterad till hur vi har definierat arbete.
Låt oss först överväga ett objekt: en boll med massa m. vi plockar bollen upp från ett bord och höjer det ett avstånd h ovanför bordet, som visas nedan. Vi har därför gjort en mängd arbete W = mgh, (detta resultat är produkten av storleken på förskjutningsvektorn (h) och den applicerade kraften (mg) – motsvarande vektorer är parallella).
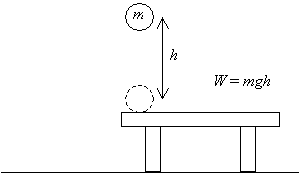
nu, om vi släpper den bollen och låter den falla från höjden h ovanför bordet, när den återgår till sin ursprungliga höjd (bordets nivå), kommer den att ha en viss hastighet v som härrör från accelerationen på grund av tyngdkraften.
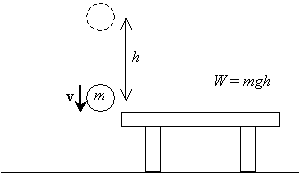
vi vill beräkna denna hastighet (eller hastighet, Tekniskt-vi kan ibland ersätta termen hastighet för hastighet, men var alltid medveten om att hastighet faktiskt är en vektor och hastighet är storleken på hastigheten). Vi vet att accelerationen på grund av tyngdkraften är konstant och att kulans initialhastighet är noll (den är stillastående innan den släpps). Vi antar att bollens ursprungliga höjd är h och att dess slutliga höjd är noll (bordets nivå). För att beräkna hastigheten genom att härleda lämpliga formler kräver vi användning av elementär integralkalkyl. (Om du är en avancerad student eller letar efter en extra utmaning kan du själv försöka härleda dessa formler under ovanstående förhållanden. Observera bara att bollens hastighet v är tidsförändringshastigheten för dess position x som en funktion av tiden t, ![]() , och att accelerationen a är tidsförändringshastigheten för hastigheten,
, och att accelerationen a är tidsförändringshastigheten för hastigheten, ![]() .)
.)
![]()
![]()
dessa formler uttrycker hastigheten som en funktion av tiden, v(t) och positionen (höjd) som en funktion av tiden, x(t), i termer av accelerationen a, höjd h och tid t. vi vet att a = –g, eftersom bollen endast accelereras av tyngdkraften och denna acceleration är nedåt (därav det negativa tecknet). Bollens slutliga position är noll meter, eller x (t) = 0. Låt oss beräkna t, tiden mellan bollens frigöring och dess ankomst till bordets nivå.
![]()
![]()
![]()
nu, låt oss beräkna hastigheten på bollen vid denna tidpunkt.
![]()
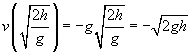
låt oss nu jämföra detta resultat med det arbete som ursprungligen gjordes på objektet: W = mgh. Observera hur nära formen dessa två uttryck är; faktiskt, den enda faktorn som saknas från hastigheten är massan av bollen, m. om vi kvadrerade hastigheten, multiplicerat med m, och sedan dividerat med 2, Vi skulle faktiskt ha samma uttryck som arbetet!
![]()
Således kan vi på något sätt se hur definitionen av kinetisk energi kan härledas. Den kinetiska energin K för ett objekt är då en skalär definierad enligt följande, där m är objektets massa och v är dess hastighet:
![]()
som det visar sig är den kinetiska energin det arbete som utförs på ett objekt av nettokraften på det objektet. Således, även om en kvinna kan göra en viss mängd arbete på ett objekt genom att lyfta det från en höjd till en annan, är nettokraften på det objektet noll (kvinnan tillämpar en kraft som är lika med men motsatt i tyngdkraftsriktningen). Således finns det ingen förändring i kinetisk energi. Om det objektet släpps och får falla, får det emellertid kinetisk energi eftersom nettokraften på det helt enkelt är tyngdkraften (en enda kraft). För att förstå förhållandet mellan kinetisk energi och arbete måste vi förfina vårt koncept av arbete något. Om vi definierar arbetet W som det totala arbetet som utförs på objektet av alla krafter (med andra ord det arbete som utförs på objektet med nätkraften), håller följande förhållande mellan arbetet W och de initiala och slutliga kinetiska energierna (Ki och Kf).
![]() där
där ![]()
således är det nätarbete som utförs på ett objekt lika med förändringen i objektets kinetiska energi (XHamster). Följande övningsproblem ger dig möjlighet att testa och tillämpa din förståelse för begreppen arbete och kinetisk energi.
Öva Problem: En projektil med massa 1 kilo reser med 5 meter per sekund. Vilken hastighet måste en 0,1 kilo projektil resa för att uppnå samma kinetiska energi?
lösning: Låt oss först beräkna den kinetiska energin hos den mer massiva (1 kilo) projektilen.
![]()
vi kan nu beräkna hastigheten på det mindre massiva objektet så att det har samma kinetiska energi, K.
![]()
![]()
![]()
Övningsproblem: en man lyfter en vikt på 15 kilo till en höjd av två meter från marken innan han släpper den. I ögonblicket innan vikten kommer i kontakt med marken, vad är dess hastighet?
lösning: Låt oss rita ett diagram som illustrerar krafterna som verkar på objektet när det lyfts och när det faller; dessa krafter inkluderar gravitation (Fg) och den uppåtgående kraften som mannen tillämpar (Fu).
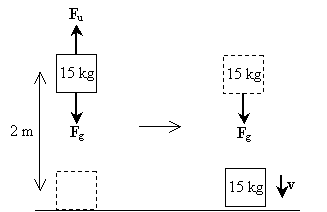
Observera att det första steget i processen (lyfta vikten) innebär ingen nettokraft som verkar på objektet-kraften på grund av tyngdkraften balanseras av den kraft som mannen tillämpar för att lyfta vikten. I det andra steget upplever emellertid vikten bara tyngdkraften. Nettokraften är i detta fall därför mg i nedåtgående riktning. Som sådan är objektets hastighet också i nedåtgående riktning. Arbetet på vikten som ett resultat av tyngdkraften är helt enkelt mgh; detta är också det totala arbetet på vikten under hela processen. Observera att den initiala kinetiska energin hos vikten är noll eftersom den har nollhastighet. Låt oss nu beräkna hastigheten genom att tillämpa förhållandet mellan nätarbete och förändringen i kinetisk energi.