Det Grunnleggende: KNN for klassifisering og regresjon

Datavitenskap fra grunnen

datavitenskap eller anvendt statistikk kurs starter vanligvis med lineære modeller, men På sin måte Er K-nærmeste naboer trolig den enkleste brukte modellen konseptuelt. KNN-modeller er egentlig bare tekniske implementeringer av en felles intuisjon, at ting som deler lignende funksjoner pleier å være, vel, lignende. Dette er neppe en dyp innsikt, men disse praktiske implementeringene kan være ekstremt kraftige, og avgjørende for noen som nærmer seg et ukjent datasett, kan håndtere ikke-lineariteter uten komplisert datateknikk eller modelloppsett.

Hva

som et illustrativt eksempel, la oss vurdere det enkleste tilfellet med Å bruke EN KNN-modell som klassifikator. La oss si at du har datapunkter som faller inn i en av tre klasser. Et todimensjonalt eksempel kan se slik ut:

du kan sikkert se ganske tydelig at de forskjellige klassene er gruppert sammen – øvre venstre hjørne av grafene ser ut til å tilhøre den oransje klassen, høyre / midtre delen til den blå klassen. Hvis du fikk koordinatene til new point et sted på grafen og spurte hvilken klasse det var sannsynlig å tilhøre, ville det meste av tiden være ganske klart. Ethvert punkt i øvre venstre hjørne av grafen er sannsynligvis oransje, etc.

oppgaven blir litt mindre sikker i mellom klassene, men der vi må avgjøre en beslutningsgrense. Vurder det nye punktet lagt til i rødt nedenfor:

skal dette nye punktet klassifiseres som oransje eller blått? Poenget ser ut til å falle mellom de to klyngene. Din første intuisjon kan være å velge klyngen som er nærmere det nye punktet. Dette ville være den ‘nærmeste nabo’ tilnærming, og til tross for å være konseptuelt enkel, det gir ofte ganske fornuftige spådommer. Hvilket tidligere identifisert punkt er det nye punktet nærmest? Det kan ikke være åpenbart bare eyeballing grafen hva svaret er, men det er lett for datamaskinen å kjøre gjennom punktene og gi oss et svar:

ser det ut til at det nærmeste punktet er i den blå kategorien, så vårt nye punkt er sannsynligvis også. Det er den nærmeste nabo-metoden.

på dette punktet lurer du kanskje på hva ‘ k ‘ i k-nærmeste naboer er for. K er antall nærliggende punkter som modellen vil se på når man vurderer et nytt punkt. I vårt enkleste nærmeste naboeksempel var denne verdien for k ganske enkelt 1-vi så på nærmeste nabo, og det var det. Du kunne imidlertid ha valgt å se på nærmeste 2 eller 3 poeng. Hvorfor er dette viktig, og hvorfor skulle noen sette k på et høyere tall? For det første kan grensene mellom klassene støte opp ved siden av hverandre på måter som gjør det mindre åpenbart at nærmeste punkt vil gi oss riktig klassifisering. Tenk på de blå og grønne områdene i vårt eksempel. Faktisk, la oss zoome inn på dem:

Legg Merke til at mens de generelle områdene virker tydelige nok, synes deres grenser å være litt sammenflettet med hverandre. Dette er et vanlig trekk ved datasett med litt støy. Når dette er tilfelle, blir det vanskeligere å klassifisere ting i grenseområdene. Vurder dette nye punktet:

på den ene siden ser det visuelt ut som det nærmeste tidligere identifiserte punktet er blått, som vår datamaskin lett kan bekrefte for oss:

På den annen side virker det nærmeste blå punktet som litt av en outlier selv, langt borte fra sentrum av den blå regionen og slags omgitt av grønne punkter. Og dette nye punktet er selv på utsiden av det blå punktet! Hva om vi så på de tre nærmeste punktene til det nye røde punktet?

Eller til og med de nærmeste fem punktene til det nye punktet?

nå ser det ut til at vårt nye punkt er i et grønt nabolag! Det skjedde å ha et nærliggende blått punkt, men overvekt eller nærliggende punkter er grønne. I dette tilfellet, kanskje det ville være fornuftig å sette en høyere verdi for k, for å se på en håndfull nærliggende punkter og få dem til å stemme på en eller annen måte på prediksjonen for det nye punktet.

problemet som illustreres er over-passende. Når k er satt til en, er grensen mellom hvilke regioner identifisert av algoritmen som blå og grønn humpete, det slanger frem med hvert enkelt punkt. Det røde punktet ser ut som det kan være i den blå regionen:

Bringer k opp til 5, men jevner ut beslutningsgrensen som de forskjellige nærliggende punktene stemmer. Det røde punktet virker nå fast i det grønne nabolaget:

handelen med høyere verdier av k er tapet av granularitet i beslutningsgrensen. Innstilling k veldig høy vil ha en tendens til å gi deg glatte grenser, men de virkelige verdensgrensene du prøver å modellere, er kanskje ikke helt glatte.

Praktisk sett kan vi bruke samme type nærmeste naboer tilnærming til regresjoner, der vi vil ha en individuell verdi i stedet for en klassifisering. Vurder følgende regresjon nedenfor:

dataene ble tilfeldig generert, men ble generert for å være lineære, så en lineær regresjonsmodell ville naturlig passe disse dataene godt. Jeg vil imidlertid påpeke at du kan tilnærme resultatene av den lineære metoden på en konseptuelt enklere måte med en k-nærmeste naboer tilnærming. Vår ‘regresjon’ i dette tilfellet vil ikke være en enkelt formel som EN OLS-modell ville gi oss, men heller en best spådd utgangsverdi for en gitt inngang. Vurder verdien av -.75 på x-aksen, som jeg har merket med en vertikal linje:

Uten å løse noen ligninger kan vi komme til en rimelig tilnærming av hva utgangen skal være bare ved å vurdere de nærliggende punktene:

det er fornuftig at den forventede verdien skal være nær disse punktene, ikke mye lavere eller høyere. Kanskje en god prediksjon ville være gjennomsnittet av disse punktene:

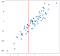
Du kan tenke deg å gjøre dette for alle mulige inngangsverdier og komme opp med spådommer overalt:

Koble alle disse spådommene med en linje gir oss vår regresjon:

i dette tilfellet er resultatene ikke en ren linje, men de sporer oppadgående helling av dataene rimelig bra. Dette kan ikke virke veldig imponerende, men en fordel med enkelheten i denne implementeringen er at den håndterer ikke-linearitet godt. Vurder denne nye samlingen av poeng:

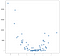
disse punktene ble generert ved å kvadrere verdiene fra forrige eksempel, men anta at du kom over et datasett som dette i naturen. Det er åpenbart ikke lineært i naturen, og mens EN OLS-stilmodell enkelt kan håndtere denne typen data, krever det bruk av ikke-lineære eller interaksjonsbetingelser, noe som betyr at datavitenskaperen må ta noen beslutninger om hva slags datateknikk som skal utføres. DEN SAMME koden jeg brukte på det lineære eksemplet kan gjenbrukes helt på de nye dataene for å gi et brukbart sett med spådommer:

som med klassifiseringseksemplene hjelper det å sette en høyere verdi k oss til å unngå overfit, selv om du kan begynne å miste prediktiv kraft på marginen, spesielt rundt kantene på datasettet. Tenk på det første eksempelet datasett med spådommer laget med k satt til en, det er en nærmeste nabo tilnærming:

våre spådommer hopper uberegnelig rundt når modellen hopper fra ett punkt i datasettet til det neste. Som kontrast, sette k på ti, slik at ti totale poeng er i gjennomsnitt sammen for prediksjon gir en mye jevnere tur:

Vanligvis ser det bedre ut, men du kan se noe av et problem på kantene av dataene. Fordi vår modell tar så mange poeng i betraktning for en gitt prediksjon, når vi kommer nærmere en av kantene på prøven vår, begynner våre spådommer å bli verre. Vi kan løse dette problemet noe ved å veie våre spådommer til de nærmere punktene, selv om dette kommer med egne avvik.

Hvordan

når du setter OPP EN KNN-modell, er det bare en håndfull parametere som må velges / kan justeres for å forbedre ytelsen.

K: antall naboer: Som diskutert, vil økende K ha en tendens til å jevne ut beslutningsgrenser, unngå overfit på bekostning av noen oppløsning. Det er ingen enkelt verdi av k som vil fungere for hvert enkelt datasett. For klassifiseringsmodeller, spesielt hvis det bare er to klasser, er et oddetall vanligvis valgt for k. dette er slik at algoritmen aldri går inn i et slips: f.eks.

Avstandsmåling: Det er, som det viser seg, forskjellige måter å måle hvor ‘ nær ‘ to punkter er til hverandre, og forskjellene mellom disse metodene kan bli betydelig i høyere dimensjoner. Mest brukte Er Euklidsk avstand, standardsorten du kanskje har lært i ungdomsskolen ved hjelp av pythagorasetningen. En annen metrisk er såkalt ‘Manhattan distance’, som måler avstanden tatt i hver kardinalretning, i stedet for langs diagonalen (som om du gikk fra en gatekryss I Manhattan til En annen og måtte følge gatenettet i stedet for å kunne ta den korteste ‘i luftlinje’ ruten). Mer generelt, disse er faktisk begge former for det som kalles ‘Minkowski avstand’, hvis formel er:

når p er satt til 1, er denne formelen den samme Som Manhattan-avstanden, og Når den er satt til To, Euklidisk avstand.

Vekter: en måte å løse både spørsmålet om en mulig ‘slips’ når algoritmen stemmer på en klasse og problemet der våre regresjonsprognoser ble verre mot kantene av datasettet, er å innføre vekting. Med vekter vil nærpunktene telle mer enn poengene lenger unna. Algoritmen vil fortsatt se pa alle k rmeste naboer, men de n rmeste naboene vil ha mer av en stemme enn de lenger unna. Dette er ikke en perfekt løsning og bringer opp muligheten for overfitting igjen. Vurder vårt regresjon eksempel, denne gangen med vekter:

våre spådommer går rett til kanten av datasettet nå, men du kan se at våre spådommer nå svinger mye nærmere de enkelte punktene. Den vektede metoden fungerer rimelig bra når du er mellom poeng, men når du kommer nærmere og nærmere et bestemt punkt, har punktets verdi mer og mer innflytelse på algoritmenes prediksjon. Hvis du kommer nær nok til et punkt, er det nesten som å sette k til en, siden det punktet har så mye innflytelse.

Skalering/normalisering: et siste, men avgjørende viktig poeng er AT KNN-modeller kan kastes av hvis forskjellige funksjonsvariabler har svært forskjellige skalaer. Vurdere en modell som prøver å forutsi, si, salgsprisen på et hus på markedet basert på funksjoner som antall soverom og den totale arealet av huset, etc. Det er mer variasjon i antall kvadratfot i et hus enn det er i antall soverom. Vanligvis har hus bare en liten håndfull soverom, og ikke engang det største herskapshuset skal ha titalls eller hundrevis av soverom. Kvadratfot, derimot, er relativt små, så husene kan variere fra nær, si, 1000 sq feat på den lille siden til titusenvis av sq fot på den store siden.

Vurder sammenligningen mellom et 2000 kvadratmeter hus med 2 soverom og et 2010 kvadratmeter hus med to soverom-10 kvm. føtter gjør knapt en forskjell. Derimot er et 2000 kvadratmeter hus med tre soverom veldig annerledes, og representerer en helt annen og muligens mer trangt layout. En naiv datamaskin ville ikke ha sammenheng for å forstå det, men. Det vil si at 3 soverom er bare ‘ en ‘enhet fra 2 soverom, mens 2,010 sq footer er’ ti ‘ fra 2,000 sq footer. For å unngå dette bør funksjonsdata skaleres før du implementerer EN KNN-modell.

Styrker og svakheter

KNN-modeller er enkle å implementere og håndtere ikke-lineariteter godt. Montering av modellen har også en tendens til å være rask: datamaskinen trenger ikke å beregne noen spesielle parametere eller verdier, tross alt. Handelen her er at mens modellen er rask å sette opp, er det tregere å forutsi, siden for å forutsi et utfall for en ny verdi, må den søke gjennom alle punktene i treningssettet for å finne de nærmeste. FOR store datasett KAN KNN derfor være en relativt langsom metode sammenlignet med andre regresjoner som kan ta lengre tid å passe, men deretter gjøre sine spådommer med relativt enkle beregninger.

Et annet problem MED EN KNN-modell er at DEN mangler tolkbarhet. EN ols lineær regresjon vil ha klart tolkbare koeffisienter som selv kan gi noen indikasjon på effektstørrelsen til en gitt funksjon (selv om det må tas litt forsiktighet ved tildeling av årsakssammenheng). Å spørre hvilke funksjoner som har størst effekt, gir imidlertid ikke mening for EN KNN-modell. Delvis på grunn AV DETTE KAN KNN-modeller heller ikke brukes til funksjonsvalg, på den måten en lineær regresjon med en ekstra kostnadsfunksjon, som ridge eller lasso, kan være, eller måten et beslutningstre implisitt velger hvilke funksjoner som virker mest verdifulle.