Kinetisk energi Er bevegelsesenergien. Et uttrykk for kinetisk energi er avledet ved å se på saken av et objekt som løftes til en relativ høyde (dermed er arbeid gjort på dette objektet) og deretter tillatt å falle.
Nøkkelbegreper
O Kinetisk energi
Mål
O Utlede et uttrykk for kinetisk energi fra fysikkbegrepet arbeid
O Forstå forholdet mellom arbeid og kinetisk energi
O Beregn kinetisk energi av ulike objekter
La oss Begynne!
Relatert Arbeid Og Kinetisk Energi
i en viss forstand er arbeid mengden energi satt inn i en oppgave (eller kanskje «satt inn i objektet»). For eksempel, tenk at vi plukke opp noen objekt av gulvet og heve den til en viss høyde; vi har gjort en viss mengde arbeid på dette objektet. Hvis vi lar det gå, akselererer det imidlertid, som om det arbeidet vi gjorde med å løfte objektet, blir omgjort til bevegelse. Gjennom dette eksemplet kan vi utlede en definisjon for kinetisk energi, som er bevegelsesenergi. Denne definisjonen, som vi vil se, er nært knyttet til hvordan vi har definert arbeid.
la Oss først vurdere et objekt: en ball med masse m. vi plukker ballen opp av et bord og hever den en avstand h over det bordet, som vist nedenfor. Vi har derfor gjort En mengde arbeid W = mgh, (dette resultatet er produktet av størrelsen på forskyvningsvektoren (h) og den påførte kraften (mg) – de tilsvarende vektorene er parallelle).
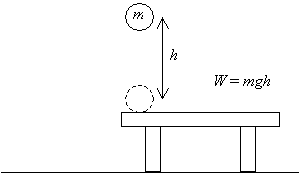
nå, hvis vi slipper den ballen og lar den falle fra høyden h over bordet, når den vender tilbake til sin opprinnelige høyde (bordets nivå), vil den ha en viss hastighet v som følge av akselerasjonen på grunn av tyngdekraften.
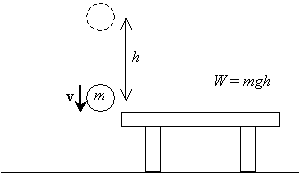
vi vil beregne denne hastigheten (eller hastigheten, teknisk-vi kan av og til erstatte termen hastighet for hastighet, men vær alltid klar over at hastighet faktisk er en vektor og hastighet er størrelsen på hastigheten). Vi vet at akselerasjonen på grunn av tyngdekraften er konstant og at ballens innledende hastighet er null (den er stasjonær før den slippes ut). Vi antar at den opprinnelige høyden på ballen er h og at den endelige høyden er null (nivået på bordet). For å beregne hastigheten ved å utlede de riktige formlene, krever vi bruk av elementær integral kalkulator. (Hvis du er en avansert student eller leter etter en ekstra utfordring, kan du prøve å utlede disse formlene under de ovennevnte forholdene selv. Bare vær oppmerksom på at hastigheten v av ballen er tidsendringshastigheten for sin posisjon x som en funksjon av tid t, ![]() , og at akselerasjonen a er tidsendringshastigheten for hastigheten,
, og at akselerasjonen a er tidsendringshastigheten for hastigheten, ![]() .)
.)
![]()
![]()
disse formlene uttrykker hastigheten som en funksjon av tid, v (t) og posisjonen (høyde) som en funksjon av tid, x (t), når det gjelder akselerasjonen a, høyde h og tid t. Vi vet at a = –g, siden ballen bare akselereres av tyngdekraften og denne akselerasjonen er nedover (dermed det negative tegnet). Den endelige posisjonen til ballen er null meter, eller x(t) = 0. La oss beregne t, hvor mye tid mellom ballens utgivelse og ankomst på bordets nivå.
![]()
![]()
![]()
nå, la oss beregne hastigheten på ballen på dette tidspunktet.
![]()
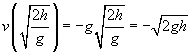
la oss nå sammenligne dette resultatet med arbeidet som opprinnelig ble gjort på objektet: W = mgh. Legg merke til hvor nær i form disse to uttrykkene er; faktisk er den eneste faktoren som mangler fra hastigheten ballens masse, m. hvis vi kvadrerte hastigheten, multiplisert med m, og deretter delt med 2, ville vi faktisk ha samme uttrykk som arbeidet!
![]()
Dermed kan vi på en måte se hvordan definisjonen av kinetisk energi kan utledes. Den kinetiske energien K til et objekt er da en skalar definert som følger, hvor m er objektets masse og v er dens hastighet:
![]()
som det viser seg, er den kinetiske energien arbeidet på et objekt av nettokraften på det objektet. Således, selv om en kvinne kan gjøre en viss mengde arbeid på et objekt ved å løfte det fra en høyde til en annen, er nettokraften på det objektet null(kvinnen bruker en kraft lik, men motsatt i tyngdekraften). Dermed er det ingen endring i kinetisk energi. Hvis det objektet frigjøres og får lov til å falle, får det imidlertid kinetisk energi fordi nettokraften på den bare er tyngdekraften (en enkelt kraft). For å forstå forholdet mellom kinetisk energi og arbeid må vi derfor forfine vårt konsept for arbeid noe. Hvis vi definerer arbeidet W som det totale arbeidet som gjøres på objektet av alle krefter (med andre ord arbeidet som gjøres på objektet av netto kraft), holder følgende forhold mellom arbeidet W Og de første og endelige kinetiske energiene (Ki og Kf).
![]() hvor
hvor ![]()
dermed er netto arbeid på et objekt lik endringen i objektets kinetiske energi (Δ). Følgende praksis problemer gir deg en mulighet til å teste og anvende din forståelse av begrepene arbeid og kinetisk energi.
Praksis Problem: Et prosjektil med masse 1 kilo reiser på 5 meter per sekund. Hvilken hastighet må en 0,1 kilo prosjektil reise for å oppnå samme kinetiske energi?
Løsning: la Oss først beregne den kinetiske energien til det mer massive (1 kilo) prosjektilet.
![]()
vi kan nå beregne hastigheten til det mindre massive objektet slik At Det har samme kinetiske energi, K.
![]()
![]()
![]()
Praksis Problem: en mann løfter en 15-kilo vekt til en høyde på to meter ut av bakken før slippe den. I øyeblikket før vekten kommer i kontakt med bakken, hva er dens hastighet?
Løsning: la oss tegne et diagram som illustrerer kreftene som virker på objektet når det løftes og faller; disse kreftene inkluderer tyngdekraften (Fg) og den oppadgående kraften som mannen bruker (Fu).
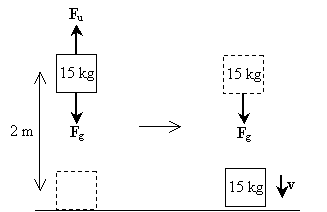
Merk at det første trinnet i prosessen (løfte vekten) innebærer ingen netto kraft som virker på objektet-kraften på grunn av tyngdekraften er balansert av kraften som mannen bruker i å løfte vekten. I det andre trinnet opplever vekten bare tyngdekraften. Netto kraft, i dette tilfellet, er derfor mg i nedadgående retning. Som sådan er objektets hastighet også i nedadgående retning. Arbeidet på vekten som følge av tyngdekraften er ganske enkelt mgh; dette er også det totale arbeidet på vekten gjennom hele prosessen. Merk at den opprinnelige kinetiske energien til vekten er null fordi den har null hastighet. La oss nå beregne hastigheten ved å bruke forholdet mellom netto arbeid og endringen i kinetisk energi.