Kunnskapsstruktur

Hentet fra et hefte som følger med en workshop for high school realfagslærere.

Av Robert J. Dufresne, William J. Leonard Og William J. Gerace

vår gruppe På UMass har utviklet en kognitiv modell som hjelper oss til å representere forskjellene på måter som eksperter og nybegynnere lagrer og bruker innholdskunnskap. Modellen hjelper oss også med å målrette bestemte områder som nybegynnere må konsentrere seg om for å bli bedre problemløsere. Modellen er imidlertid bare en representasjon av kunnskapsstrukturen, og den utvikler seg kontinuerlig. Dermed må det ikke tas for bokstavelig. Dens nytte kommer fra dens evne til å gi en konkret manifestasjon, men ufullkommen, av måtene som eksperter og nybegynnere tenker på. Modellen hjelper oss å diskutere:

1. lagring av domenespesifikk kunnskap;
2. ekspert-og nybegynnerlignende problemløsningsadferd;
3. den hierarkiske strukturen til en eksperts kunnskapsbutikk;
4. misoppfatninger;
5. effektene av målfrie og målrettede spørsmål; og
6. meta-kommunikasjonsprosessen.

i denne workshopen—og i vår tilnærming til fysikk generelt – – – er det 3 grunnleggende temaer:

1. Spesielle typer kunnskap og kunnskapsstrukturer er nødvendig for dyktig problemløsning. Mye av denne kunnskapen er konseptuell i naturen, i motsetning til operasjonell eller prosessuell, og kraftige kunnskapsstrukturer involverer nødvendigvis konseptuelle elementer. Tilstedeværelsen av konseptuelle elementer i kunnskapsstrukturene er nøkkelen til å ha en» dypere forståelse » av fysikk.
2. Spesielle typer kognitive prosesser er nødvendig for tilegnelse av konseptkunnskap og bygging av nyttige kunnskapsstrukturer.
3. det er mulig å designe aktiviteter som fremmer disse ønskelige kognitive prosessene. I mange tilfeller er disse aktivitetene bare aktualiseringer av de kognitive prosessene selv. (Dette punktet vil forhåpentligvis bli tydeligere senere.)

Vi vil utdype hvert av disse temaene før vi fokuserer på konkrete eksempler.

Tema 1: hva trenger elevene å vite og hvordan skal det de vet være strukturert for effektiv problemløsning?

vi begynner med å identifisere noen av de ulike typer kunnskap som elevene trenger å vite:

• Konseptuell kunnskap, som begrepet momentum eller energi, eller at hastigheten til et objekt endres når det akselererer, eller at gravitasjonspotensialenergien til et objekt avtar når den faller.
• faktakunnskap, som verdien av gravitasjonskonstanten g, månens radius eller tettheten av jern.
• Representasjonskunnskap, for eksempel hvordan tegne og bruke grafer.
• Strategisk kunnskap, som evnen til å gjenkjenne anvendelsen av et konsept, som momentum er bevart når det ikke er noen eksterne krefter, eller at energi er bevart når det ikke er noen ikke-konservative krefter.
• Meta-kognitiv kunnskap, for eksempel bevissthet om underliggende forutsetninger, eller at et svar bør kontrolleres ved å løse problemet på en annen måte.
• selvkunnskap, for eksempel å vite ens sannsynlige kilder til feil, eller å vite at man bør være mer prosessorisk når man løser problemer.
• operasjonell kunnskap, for eksempel hvordan man tar kryssproduktet eller prikkproduktet av to vektorer, eller hvordan man tar determinanten til en matrise, eller hvordan man tegner et fritt kroppsdiagram.
• Prosedyrekunnskap, for eksempel når man skal bruke bevaring av energi (dvs., når alle krefter er konservative), eller når man skal spesifisere et koordinatsystem (f.eks. når man finner potensiell energi), eller når man skal tegne et fri-kroppsdiagram (f. eks. når man bruker Newtons Lover).
• Problemstatskunnskap, som er funksjonene til et problem som brukes til å bestemme hvordan man løser det. Eksempler er: å vite at det ikke er noen eksterne krefter i et bestemt problem, eller at det ikke er noen ikke-konservative krefter i problemet, eller at et objekt er i ro i utgangspunktet, eller at objektet er i en skråning.

denne typen kunnskap må organiseres og struktureres for effektiv bruk ved problemløsning. For å diskutere de organisatoriske og strukturelle aspektene av kunnskap, har vi funnet det praktisk å klassifisere disse typene i tre generelle kategorier. Vi kaller disse tre gruppene: Konseptuell Kunnskap, Operasjonell Og Prosessuell Kunnskap og Problemstatlig Kunnskap. I Fig. 1, disse tre generelle kategoriene vises i en representasjon av hvordan eksperter lagrer innholdskunnskap.

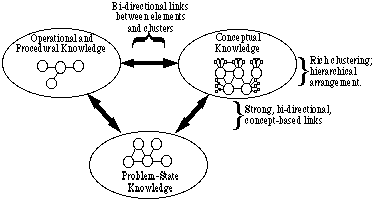Fig. 1: En representasjon av en eksperts kunnskapsstruktur

eksperten har en rik klynging av begreper, hvor hvert konsept er relatert til mange andre begreper, og forholdet mellom begreper er tydelig forstått. Konsepter er ordnet hierarkisk ved hjelp av paraplykonsepter for å tettere forholde seg til dem. Faktisk brukes paraplykonsepter til å gruppere elementer innenfor hver av de tre kategoriene. Eksperten har et stort lager av problemstatlig kunnskap, inkludert mye informasjon om hvilke prinsipper som gjelder for bestemte situasjoner. Eksperten har også en stor butikk av ligninger, operasjoner og prosedyrer (EOPs) som kan nås raskt.

koblingene mellom hvert par kategorier er svært sterke: Problemstater er sterkt knyttet til konsepter og Til EOPs, som selv er sterkt knyttet til hverandre. De samme paraplybegrepene brukes til å gruppere konsepter, problemtilstander og EOPs. Derfor, for et bestemt problem, kan begreper brukes til å bestemme hensiktsmessigheten og anvendeligheten av ligninger, og bruken av spesifikke operasjoner og prosedyrer.

(man må være veldig forsiktig her for ikke å være for stiv i sin tenkning, fordi det er lett å være uenig om hvilken av disse kategoriene som skal brukes til å klassifisere et bestemt element av kunnskap, eller om det bare tilhører en kategori. Vårt formål er rett og slett å ha en mekanisme for å visualisere flere nivåer av tilknytning som kan oppstå mellom elementer.)

vi pleier å bruke begrepet kobling til å bety en formet tilknytning mellom to elementer av samme eller forskjellige kunnskapstyper, og begrepet clustering for å referere til foreninger mellom flere elementer eller klynger. Hva gjør denne typen diskusjon svært vanskelig er at det er en slags iterativ prosess som skjer her: Et veldig sterkt bånd mellom tre elementer-en konseptuell klynge, anerkjennelsen av omstendighetene som gjør konseptet aktuelt, og prosedyrene som trengs for å anvende konseptet-danner en ny type kunnskapselement som vi legger Inn I Strategisk Kunnskap (en fjerde kategori). Dette nye kunnskapselementet er det noen refererer til som et skjema, og innebærer ofte også problemstatlig kunnskap. Siden kunnskapselementet er konseptuelt i naturen, blir det replikert (dvs. gjentatt) i den konseptuelle boblen.

hvis vi ser nærmere på den konseptuelle boblen, ser vi noen av de spesifikke typene konseptuell kunnskap, For Eksempel Representativ Kunnskap, Strategisk Kunnskap, Metakognitiv Kunnskap og Kunnskap Om Grunnleggende Begreper. Dette er representert I Fig. 2. (Andre typer konseptuell kunnskap vises ikke.)

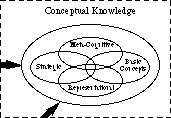Fig. 2: typer konseptkunnskap

Hvordan er en nybegynners kunnskapsstruktur forskjellig fra en ekspert? Som representert I Fig. 3, nybegynnere generelt har en dårlig clustering av begreper. Mange lenker er upassende; andre er ikke-eksisterende. Noen av de upassende koblingene er ekstremt sterke, noe som fører til misforståelser. Nybegynnere bruker vanligvis ikke paraplybegreper til å gruppere elementer. De har en liten butikk av problemssituasjoner, der overflatefunksjoner brukes til å samle dem sammen og bestemme hvordan problemer skal løses. De er kjent med et relativt stort antall ligninger, men de husker ofte dem feil eller må slå dem opp for å kunne bruke dem. De har blitt undervist i operasjoner og prosedyrer, men de er ennå ikke dyktige på dem. Derfor kan det ikke sies at de «kjenner» dem.

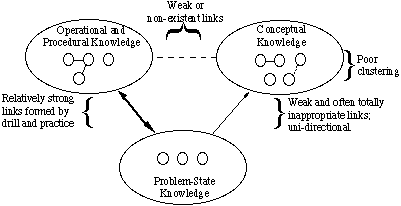Fig. 3: en representasjon av nybegynnerens kunnskapsstruktur

Koblinger mellom konsepter og EOPs er svake eller ikke-eksisterende. Koblinger mellom begreper og problemssituasjoner er også svake. Dermed kan en nybegynner ikke analysere et problem og kan ikke bestemme hensiktsmessigheten til bestemte ligninger. Koblingene mellom problemssituasjoner og EOPs er relativt sterke, men koblingene er hovedsakelig basert på mengdene som ligningene har til felles med givens og eksplisitte ukjente av problemet.

Tema 2: I hvilke typer kognitive prosesser må studentene engasjere seg for å utvikle hensiktsmessige kunnskapsstrukturer?

for å svare på dette spørsmålet må vi først forstå hvordan eksperter og nybegynnere løser problemer annerledes.

Nybegynnere er generelt mislykket når de prøver å løse typiske problemer i fysikk. Bruke Modellen til å representere prosessen, hvordan løser en typisk nybegynner et problem? Fordi de sterkeste koblingene i nybegynnerens kunnskapsstruktur er mellom problemssituasjoner og ligninger, foreslår lesing av et problem umiddelbart ligninger som involverer mengdene (kjent og ukjent) eksplisitt gitt i problemet. Uten å bestemme anvendeligheten av disse ligningene, og uten å prøve å tenke på andre ligninger som kan innebære de samme mengdene, begynner nybegynneren vanligvis å manipulere de mest kjente ligningene til det ukjente kan løses for. Den siste ligningen som er dekket i klassen, er den lettest tilgjengelige og den raskest tilbakekalte. Dermed ser nybegynneren etter og (hvis «vellykket») bare finner en måte å løse et problem på og stopper vanligvis uten å undersøke andre muligheter og uten å analysere problemssituasjonen. Ligningene funnet på denne måten er ofte upassende fordi nybegynnere ofte ikke bruker konsepter for å rettferdiggjøre deres søknad. Selv om elevene blir drevet til å påkalle konsepter ved å analysere problemer på forhånd, er deres lenker til EOPs generelt for svake til å være nyttige for problemløsing. Også koblinger mellom konsepter og problemssituasjoner er uni-directional, så analogier er ikke spesielt nyttige: Nybegynnere kan ikke bruke analogier til å løse problemer fordi de ikke kan identifisere hvilke av problemene de allerede har løst, er konseptuelt lik den de prøver å løse. I stedet bruker nybegynnere overflatefunksjoner for å etablere «likhet» og forsøke å løse nye problemer basert på deres likhet med overflatefunksjonene til problemer de allerede har løst.

fordi eksperter klassifiserer problemer og EOPs i henhold til de samme paraplybegrepene, kan de ofte gå direkte fra problemssituasjoner til passende ligninger, operasjoner og/eller prosedyrer. Fordi koblingene mellom ulike kategorier er sterke, kan vanskelige problemer (de som en direkte kobling mellom problemtilstander og Eop ikke eksisterer) løses ved bevisst å påkalle konsepter, og dermed indirekte koble problemtilstander til de aktuelle EOP(ene). Fordi koblingene mellom konsepter og problemssituasjoner er toveis, er analogier et ekstremt nyttig problemløsningsverktøy for eksperter. Til slutt har eksperter vanligvis mer enn en tilnærming til å løse et bestemt problem.

her er en oppsummering av de store forskjellene mellom eksperter og nybegynnere:

1. Nybegynnere har en dårlig klynging av konsepter, noe som ofte fører til misforståelser. Eksperter har en rik clustering av konsepter, problemssituasjoner, ligninger, prosedyrer og operasjoner, noe som fører til forbedret problemløsende evne.
2. Nybegynnere har vanligvis bare en måte å løse et bestemt problem på, mens eksperter ofte kan finne mer enn en måte. Derfor kan eksperten forsøke å løse uoverensstemmelser når de oppstår og sjekke svar, mens nybegynnere ikke er klar over at uoverensstemmelser eksisterer og ikke kan kontrollere svarene sine.
3. Nybegynnere bruker ofte ligningsmanipulering og bruker sjelden konseptbaserte strategier for å få svar. Eksperten bruker konsepter og analogier for å foreslå flere løsningsmetoder og planlegger en strategi for å finne det riktige svaret.
4. Nybegynnere mislykkes ofte i å få det riktige svaret, og når De får det riktige svaret, kan det lett være av feil grunn. Når nybegynneren får det riktige svaret av feil grunn, blir misforståelser forsterket og blir enda vanskeligere å overvinne. En ekspert får vanligvis det riktige svaret og kan forklare hvorfor svaret er riktig.

det finnes en rekke kognitive prosesser som er gunstige for å hjelpe nybegynnere med å utvikle en konseptbasert problemløsende tilnærming, som vi deler inn i tre kategorier: Analyseprosesser, Resonneringsprosesser og Metakognitive Prosesser.

Analyseprosesser

• Problemanalyse, for eksempel å bygge en problemrepresentasjon.
• Konseptanalyse, for eksempel bruk av begreper for å bestemme kvalitativ oppførsel av fysiske objekter eller for å danne en strategi.
• Strategisk analyse, som å identifisere og rettferdiggjøre fysikkprinsipper som er relevante for en problemstilling.
• Representasjonsanalyse, for eksempel å utforske ulike representasjoner av et problem.
• Kompleks konstruktiv analyse, slik som å dekomponere en kompleks situasjon til enklere.

Resonneringsprosesser

• Sammenligne og kontrastere, for eksempel å identifisere hvordan elementer, situasjoner eller forhold er like og / eller forskjellige.
• Tolking, for eksempel ved å Bruke formen på et plott av posisjon vs. tid for å estimere akselerasjonen av objektet.
• Spesielle og begrensende tilfeller, det vil si å utforske ekstreme og / eller kjente forhold.
• Prototype og moteksempler, for eksempel generering av arketypiske kategorier.
• Generalisering, det vil si å gjenkjenne de fremtredende egenskapene til en omstendighet eller situasjon.

Meta-kognitive prosesser

• Refleksjon, det vil si selvstyrt gjennomgang av formål, mål, effekter av erfaring, etc.
• Meta-kommunikasjon, som er bevisst deltakelse i å etablere og raffinere kommunikasjonslinjer med læreren og andre studenter, og i å bestemme målene for læring.
• Egenevaluering, for eksempel evaluering av ens ytelse, eller identifisering av årsaker til at vanskeligheter oppstod mens du løste et problem.

Disse og andre prosesser oppfordres av våre læreplanmaterialer. De spesifikke typer aktiviteter for å gjøre dette presenteres i neste avsnitt.

Tema 3: Hvilke typer læringsaktiviteter eller erfaringer fremmer disse gunstige kognitive prosessene?

følgende aktiviteter kan brukes av lærere til å stimulere kognitive prosesser som trengs for å utvikle en konseptuell forståelse av fysikk:

1. Bruk flere representasjoner. En representasjon kan være språklig, abstrakt, symbolsk, billedlig eller konkret. Ved å bruke mange forskjellige representasjoner for samme kunnskap, og å få studenter til å oversette mellom representasjoner, hjelper studenten til å relatere kunnskapstyper og relatere kunnskapen til fysisk erfaring. Det oppfordrer dannelsen av koblinger mellom kunnskapselementer og fremmer en rik klynging av kunnskap.
2. Gjør forover og bakover referanser. Konsepter krever lang tid å bli dannet. Dermed kan du ikke vente for elevene å helt lære ett emne før du går videre til neste. Ved å gjøre frem referanser, du forberede studenten for nytt materiale. Ved å lage bakoverreferanser knytter du nytt materiale til etablert (eller delvis etablert) materiale, og gjør dermed kunnskap sammenvevd og sammenkoblet, i stedet for lineær.
3. Utforsk utvidede sammenhenger. Begreper kan være ekstremt kontekstavhengige og blir ikke globalt nyttige før de er abstrahert. Undersøke en bred sammenheng med anvendbarhet hjelper studenten å avgrense og abstrakte begreper. Det unngår også feil eller forenklede generaliseringer.
4. Sammenligne og kontrast. Vesentlig for prosessen med å strukturere (eller omstrukturere) kunnskap er klassifisering og interrelasjon av kunnskapselementer. Sammenligninger og kontraster sensibilisere elevene til kategorier og relasjoner, og hjelper elevene oppfatter fellestrekk og forskjeller som trengs for å organisere sin kunnskap butikken.
5. Kategorisere og klassifisere. Parallelt med sammenligninger og kontraster må studentene være oppmerksomme på kategorier og klassifikasjonssystemer. Studentene må også øve på å skape og gjenkjenne kategoriseringssystemer. Ved å kreve elevene til å klassifisere elementer, å velge navn for sine kategorier, og for å forklare deres system, kan vi hjelpe elevene re-strukturere sin kunnskap butikken.
6. Forutsi & Vis (utilstrekkelighet av gammel modell). Nøye utvalgte demonstrasjoner og eksperimenter kan brukes til å få frem uoverensstemmelser i studentmodeller. Studentene skal vises et oppsett eller eksperimentelt apparat og bør bli bedt om å forutsi hva som vil skje når noe er gjort. Det er viktig at elevene gjør spådommer på forhånd, og dermed gjøre dem oppmerksomme på sin egen modell. Studentene vil vurdere alternative oppfatninger bare hvis deres egne mislykkes. Å kreve at elevene bruker modellene sine og viser dem hvordan modellene deres er inkonsekvente eller utilstrekkelige, vil forberede dem til å skape bedre (men fortsatt sine egne) modeller.

7. Forklar (oppsummer, beskriv, diskuter, definer osv.). Vanlige problemer forteller sjelden læreren hva elevene ikke forstår. Selv når elevene får et problem riktig, kan det fortsatt være forvirring om anvendeligheten av ligningene som brukes. Å kreve at elevene forklarer hvordan de skal løse et problem, avslører misforståelser og misforståelser, og hjelper elevene med å omorganisere sin kunnskapsbutikk. I tillegg ser studentene sjelden i standard demonstrasjoner og eksperimenter hva eksperter ser. Elevene bør forklare og diskutere hva de tror de har sett (Under Predict & Show, For eksempel), slik at læreren kan samhandle med elevenes modeller. Videre er prosessen med å forklare (eller oppsummere, beskrive, diskutere, etc.) hjelper elevene å bli klar over sine egne modeller, så vel som modeller av andre studenter.

8. Generere flere løsninger. Effektiv problemløsning kan ikke skje med mindre studentene velger fra et sett med gyldige løsningsbaner. Ved å løse problemer på mer enn en måte lærer elevene å prioritere elementer av Deres Strategiske Kunnskap.

9. Planlegg, rettferdiggjør og strategiser. Svært få relasjoner i fysikk er alltid gyldige. For å unngå ligningsmanipulering bør studentene bli bedt om å planlegge (og deretter forklare) hvordan de vil løse problemer. Studentene må lære å bestemme hvilke begreper som er relevante (og som er irrelevante) for en bestemt problemstilling og hvordan man implementerer de relevante konseptene for å løse det problemet. Å ha elevene generere sine egne strategier hjelper dem til å lære hvordan begreper brukes til å løse problemer.
10. Reflektere (evaluere, integrere, utvide, generalisere, etc.) Etter å ha fullført de fleste aktiviteter, har studentene nytte av å se tilbake på hva de har gjort. Hvilke mønstre har de oppfattet? Hvilke generelle regler kan bygges? Andre typer aktiviteter gir studentene brikkene som trengs for å skape et sammenhengende bilde av fysikk, men en slags reflekterende aktivitet er vanligvis nødvendig for å «sette brikkene sammen».
11. Meta-kommunisere om læringsprosessen. For å lære fysikk (eller et annet komplekst emne), må studentene bli selvinvestert. De må være utsatt for andres (lærerens og studentens) modeller. De må advares om at presisjon i kommunikasjon er viktig; de må informeres om vanlige fallgruver og feiltolkninger; og de må bli fortalt at de bør re-strukturere sin kunnskap. Elevene må lære hvordan de lærer best.